人教版数学九年级上册 24.3正多边形和圆 （同步课件+练习+教案）

24.3 正多边形和圆

一．选择题

周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是（　　）

A．S3＞S4＞S6    B．S6＞S4＞S3    C．S6＞S3＞S4      D．S4＞S6＞S3

2．正多边形的中心角与该正多边形一个内角的关系是（　　）

A．互余     B．互补     C．互余或互补    D．不能确定

3．正三角形的高、外接圆半径、边心距之比为（　　）

A．3：2：1    B．4：3：2    C．4：2：1    D．6：4：3

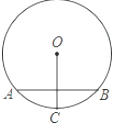
4．如图，⊙O的一条弦AB垂直平分半径OC，且AB=，则这个圆的内接正十二边形的面积为（　　）

5.下列说法正确的是（　　）

A．圆内接正六边形的边长与该圆的半径相等

B．在平面直角坐标系中，不同的坐标可以表示同一点

C．一元二次方程ax2+bx+c=0（a≠0）一定有实数根

D．将△ABC绕A点按顺时针方向旋转60°得△ADE，则△ABC与△ADE不全等

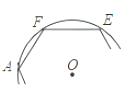
6．正六边形ABCDEF内接于⊙O，正六边形的周长是12，则⊙O的半径是（　　）

7．蜂巢的构造非常美丽、科学，如图是由7个形状、大小完全相同的正六边形组成的网络，正六边形的顶点称为格点，△ABC的顶点都在格点上．设定AB边如图所示，则△ABC是直角三角形的个数有（　　）

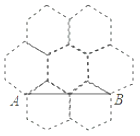
A．4个     B．6个    C．8个   D．10个

二．填空题

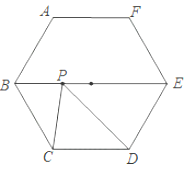
8．如图，在边长为2的正六边形ABCDEF中，点P是其对角线BE上一动点，连接PC、PD，则△PCD的周长的最小值是____

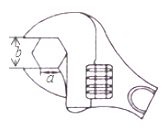
9．如图，要拧开一个边长为a=6cm的正六边形螺帽，扳手张开的开口b至少为_______cm.

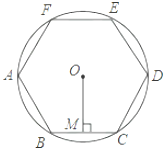
10．如图，正六边形ABCDEF内接于⊙O，⊙O的半径为6，则这个正六边形的边心距OM的长为_______。

三．解答题

11．如图，⊙O半径为4cm，其内接正六边形ABCDEF，点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，连接PB，QE，PE，BQ．设运动时间为t（s）．

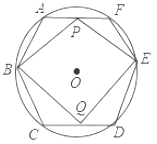
（1）求证：四边形PEQB为平行四边形；

（2）填空：

①当t=_____s时，四边形PBQE为菱形；

②当t=_____s时，四边形PBQE为矩形．

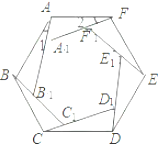
12．如图的花环状图案中，ABCDEF和A1B1C1D1E1F1都是正六边形．

（1）求证：∠1=∠2；

（2）找出一对全等的三角形并给予证明．

参考答案

一．选择题

1．B；2．B；3．A；4．C；5．A；6．B；7．D；

二．填空题

8．6；9．；10．；

三．解答题

11．解：（1）证明：∵正六边形ABCDEF内接于⊙O，

∴AB=BC=CD=DE=EF=FA，∠A=∠ABC=∠C=∠D=∠DEF=∠F，

∵点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，

∴AP=DQ=t，PF=QC=4-t，

在△ABP和△DEQ中，

AB＝DE,∠A＝∠D ,AP＝DQ，

∴△ABP≌△DEQ（SAS），

∴BP=EQ，同理可证PE=QB，

∴四边形PEQB是平行四边形．

（2）解：①当PA=PF，QC=QD时，四边形PBEQ是菱形时，此时t=2s．

②当t=0时，∠EPF=∠PEF=30°，

∴∠BPE=120°-30°=90°，

∴此时四边形PBQE是矩形．

当t=4时，同法可知∠BPE=90°，此时四边形PBQE是矩形．

综上所述，t=0s或4s时，四边形PBQE是矩形．

故答案为2s，0s或4s．

12．解：（1）证明：∵多边形ABCDEF与A1B1C1D1E1F1都是正六边形，

∴∠1+∠A1AF=120°，∠2+∠A1AF=∠B1A1F1=120°，

∴∠1+∠A1AF=∠2+∠A1AF，

即∠1=∠2；

（2）解：△ABB1≌△FAA1．

证明：∵∠F1A1B1=∠A1B1C1=120°，

∴∠AB1B=∠FA1A=60°，

则 ∠AB1B＝∠FA1A ∠1＝∠2 AB＝FA   ，

∴△ABB1≌△FAA1．