数学9.14 公式法评课ppt课件

这是一份数学9.14 公式法评课ppt课件，共29页。PPT课件主要包含了教学目标，教学流程，课堂小结，逐点讲练，知识回顾，PARTONE，平方差公式，整式乘法，因式分解，例题1等内容，欢迎下载使用。

1.了解运用公式法的含义。 2.理解平方差公式的意义，弄清公式的形式和特点，会初步运用平方差公式分解因式。3.使学生会分析和判断一个多项式是否为完全平方式，初步掌握运用完全平方式把多项式分解因式的方法；4.理解完全平方式的意义和特点，形成判断能力。5.通过运用公式法分解因式的教学，进一步体会“把一个代数式看作一个字母”的换元思想。教学重点和难点1.正确运用平方差公式分解因式。2.能辨认完全平方公式，并正确运用完全平方公式分解因式。
1、什么叫把多项式分解因式?
把一个多项式化成几个整式的积的形式，叫做多项式的分解因式.
2、已学过哪一种分解因式的方法?
思考：如何将a2-b2、 4x2-9y2分解因式？
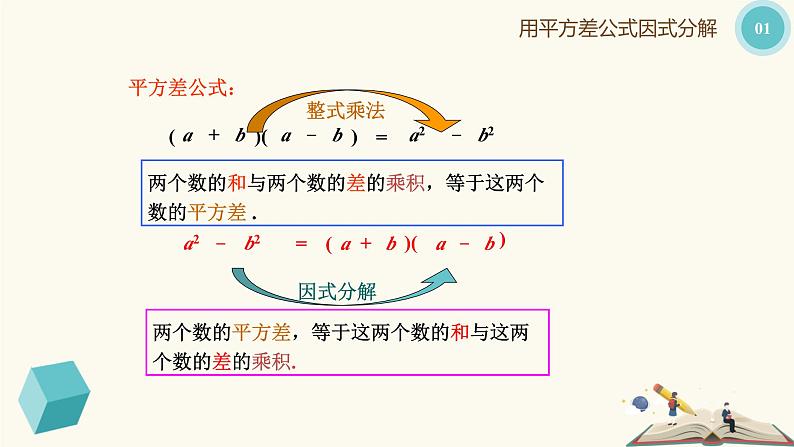
(a+b)(a－b)=a2－b2
a2－b2= (a+b)(a－b)
这种分解因式的方法称为公式法.
两个数的和与两个数的差的乘积，等于这两个数的平方差 .
两个数的平方差，等于这两个数的和与这两个数的差的乘积.
把下列各式因式分解:(1)25－16x2； (2)9a2－ b2.
(1) 25－16x2＝ 52－(4x)2＝(5＋4x)(5－4x)；
(2)9a2－ b2＝ (3a)2－( b)2＝(3a＋ b)(3a－ b)
(3) (m－a)2－(n＋b)2；
(3)(m－a)2－(n＋b)2＝[(m－a)＋(n＋b)]·[(m－a) －(n＋b)]＝(m－a＋n＋b)(m－a－n－b)．
利用平方差公式分解两项式的一般步骤：1. 找出公式中的a、b;2. 转化成a2－b2的形式；3. 根据公式a2－b2＝(a＋b) (a－b) 写出结果.
把下列各式因式分解：(1)9(m＋n)2－(m－n)2； (2) 2x3－8x.
(1) 9(m＋n)2－(m－n)2 ＝[3(m＋n)]2－(m－n)2＝ [3(m＋n)＋(m－n)] [3(m＋n)－(m－n)]＝ (3m＋3n＋m－n)(3m＋3n－m＋n)＝(4m＋2n)(2m＋4n)＝4(2m＋n)(m＋2n); (2)2x3－8x＝2x(x2－4) ＝ 2x(x2－22) ＝2x (x＋2)(x－2)
（3）－16x4＋81y4.
方法一：－16x4＋81y4＝－(16x4－81y4) ＝－(4x2＋9y2)(4x2－9y2) ＝－(4x2＋9y2)(2x＋3y)(2x－3y)．方法二：－16x4＋81y4＝81y4－16x4＝(9y2＋4x2) (9y2－4x2)＝(9y2＋4x2)(3y＋2x)(3y－2x)．
1.下列各式不能用平方差公式分解因式的是(　　)A．－x2＋y2 B．x2－(－y)2 C．－m2－n2 D．4m2－ n2
2.下列各式中，可用平方差公式分解因式的有(　　)①－a2－b2；②16x2－9y2；③(－a)2－(－b)2；④－121m2＋225n2；⑤(6x)2－9(2y)2.A．5个 B．4个 C．3个 D．2个
3.如图，在一块边长为a cm的正方形纸片的四角，各剪去一个边长为b cm的正方形，求剩余部分的面积. 如果a＝3.6，b＝0.8 呢？
剩余部分的面积为a2－4b2＝(a＋2b)(a－2b)(cm2)．当a＝3.6，b＝0.8时，剩余部分的面积为a2－4b2＝(3.6＋1.6)×(3.6－1.6)＝5.2×2＝10.4(cm2)．
4.把下列各式因式分解：(1) a2b2－m2；(2) x2－(a＋b－c)2.
(1)a2b2－m2＝(ab＋m)(ab－m)．
(2)x2－(a＋b－c)2＝[x＋(a＋b－c)][x－(a＋b－c)] ＝(x＋a＋b－c)(x－a－b＋c)．
5.把x3－9x分解因式，结果正确的是(　　) A．x(x2－9) B．x(x－3)2 C．x(x＋3)2 D．x(x＋3)(x－3)
6.将(a－1)2－1分解因式，结果正确的是(　　)A．a(a－1) B．a(a－2)C．(a－2)(a－1) D．(a－2)(a＋1)
用完全平方公式因式分解
我们可以通过以上公式把“完全平方式”分解因式我们称之为：运用完全平方公式分解因式 .
把下列完全平方式因式分解：(1)x2＋14x＋49； (2)(m＋n)2－6(m＋n)＋9.
(1)x2＋14x＋49 ＝ x2＋2×7x＋72 ＝ (x＋7) 2 ；
(2)(m＋n)2－6(m＋n)＋9＝ [(m＋n)－3]2＝(m＋n－3)2.
带平方的项符号相同（同“+”或同“-”）
用公式法正确分解因式关键是什么？
都有两项可化为两个数(或整式)的平方,另一项为这两个数(或整式)的乘积的2倍.
1.下列各式能用完全平方公式进行因式分解的是(　　)A．x2＋1 B．x2＋2x－1C．x2＋x＋1 D．x2＋4x＋4
2.把多项式x2－6x＋9分解因式，结果正确的是(　　)A．(x－3)2 　　　　 　B．(x－9)2C．(x＋3)(x－3) 　　　D．(x＋9)(x－9)
3.把2xy－x2－y2因式分解，结果正确的是(　　)A．(x－y)2 B．(－x－y)2C．－(x－y)2 D．－(x＋y)2
4.把多项式(a＋b)2－4(a2－b2)＋4(a－b)2因式分解的结果为(　　)A．(3a－b)2 B．(3b＋a)2C．(3b－a)2 D．(3a＋b)2
5.把下列各式因式分解：(1)x2－12xy＋36y2；(2)16a4＋24a2b2＋9b4；(3)－2xy－x2－y2；(4)4－12(x－y)＋9(x－y)2.
(1) x2－12xy＋36y2＝(x－6y)2.(2) 16a4＋24a2b2＋9b4＝(4a2＋3b2)2.(3) －2xy－x2－y2＝－(2xy＋x2＋y2) ＝－(x2＋2xy＋y2)＝－(x＋y)2.(4) 4－12(x－y)＋9(x－y)2＝[3(x－y)－2]2 ＝(3x－3y－2)2.
因式分解的一般步骤：1.先提：若多项式有公因式，应先提取公因式；2.再用：若还能运用公式，应再运用公式进行分解；3.三彻底：要把每一个因式分解到不能分解为止.
把下列各式因式分解：(1)3ax2＋6axy＋3ay2；(2)－x2－4y2＋4xy.
(1)3ax2＋6axy＋3ay2 ＝ 3a(x2＋2xy＋y2)＝3a(x＋y)2；
(2)－x2－4y2＋4xy＝ －(x2＋4y2－4xy)＝ －(x2－4xy＋4y2)＝－[x2－2·x·2y＋(2y)2]＝ －(x－2y)2.
把8a3－8a2＋2a进行因式分解，结果正确的是(　　)A．2a(4a2－4a＋1) B．8a2(a－1)C．2a(2a－1)2 D．2a(2a＋1)2
1. 分解因式：(a＋b)2－4a2.
(a＋b)2－4a2＝(a＋b)2－(2a)2＝(a＋b＋2a)(a＋b－2a)＝(3a＋b)(b－a)．
易错点：忽视系数变平方的形式导致出错
2. 分解因式： a4－1.
a4－1＝(a2＋1)(a2－1)＝(a2＋1)(a＋1)(a－1)．
易错点：分解不彻底导致出错
3.有下列式子：①－x2－xy－y2；② a2－ab＋ b2；③－4ab2－a2＋4b4；④4x2＋9y2－12xy；⑤3x2＋6xy＋3y2.其中在实数范围内能用完全平方公式分解因式的有(　　)个．A．1 B．2 C．3 D．4
易错点：对完全平方式的特征理解不透导致出错
②④⑤能用完全平方公式分解因式．本题容易忽视②⑤，注意②提出 ，⑤提出3以后就能利用完全平方公式分解因式．
应用平方差公式分解因式的注意事项：(1)等号左边： ①等号左边应是二项式； ②每一项都可以表示成平方的形式； ③两项的符号相反．(2)等号右边是等号左边两底数的和与这两个数的 差的积．
完全平方公式法：两个数的平方和加上(或减去)这两个数的积的2倍，等于这两个数的和(或差)的平方．即：a2±2ab＋b2＝(a±b)2.