2022-2023学年山东省青岛市即墨区七年级（下）期末数学试卷（含解析）

这是一份2022-2023学年山东省青岛市即墨区七年级（下）期末数学试卷（含解析），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年山东省青岛市即墨区七年级（下）期末数学试卷
一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列运算正确的是(    )
A. a−(b+c)=a−b+c B. 2a2⋅3a3=6a5
C. a3+a3=2a6 D. (x+1)2=x2+1
2. 下面四个图形分别是低碳、节水、节能和绿色食品标志，在这四个标志中，是轴对称图形的是(    )
A. B. C. D.
3. 已知空气的单位体积质量是0.001239g/cm3，将该数用科学记数法可以表示(    )
A. 1.239×10−3g/cm3 B. 1.239×10−2g/cm3
C. 0.1239×10−2g/cm3 D. 12.39×10−4g/cm3
4. 掷一枚质地均匀的硬币20次，下列说法正确的是(    )
A. 每2次必有1次正面向上 B. 必有10次正面向上
C. 不可能有20次正面向上 D. 可能有10次正面向上
5. 如图，有以下四个条件：①∠B+∠BCD=180°，②∠1=∠2，③∠3=∠4，④∠B=∠5，其中能判定AB//CD的条件的个数有(    )


A. 1 B. 2 C. 3 D. 4
6. 已知三角形的两边长分别为1和4，第三边长为整数，则该三角形的周长为(    )
A. 7 B. 8 C. 9 D. 10
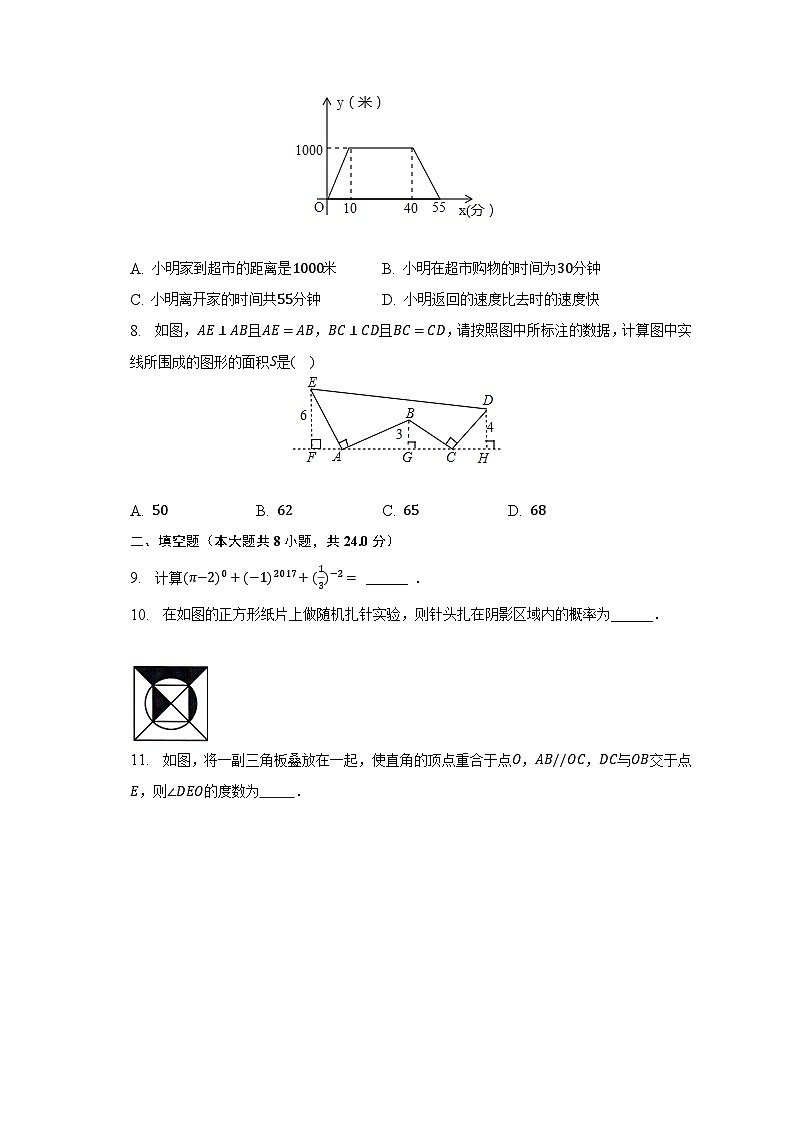
7. 小明从家里出发到超市进行购物后返回，小明离开家的路程y(米)与所用时间x(分)之间的关系如图，则下列说法不正确的是(    )

A. 小明家到超市的距离是1000米 B. 小明在超市购物的时间为30分钟
C. 小明离开家的时间共55分钟 D. 小明返回的速度比去时的速度快
8. 如图，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是(    )

A. 50 B. 62 C. 65 D. 68
二、填空题（本大题共8小题，共24.0分）
9. 计算(π−2)0+(−1)2017+(13)−2= ______ ．
10. 在如图的正方形纸片上做随机扎针实验，则针头扎在阴影区域内的概率为______．


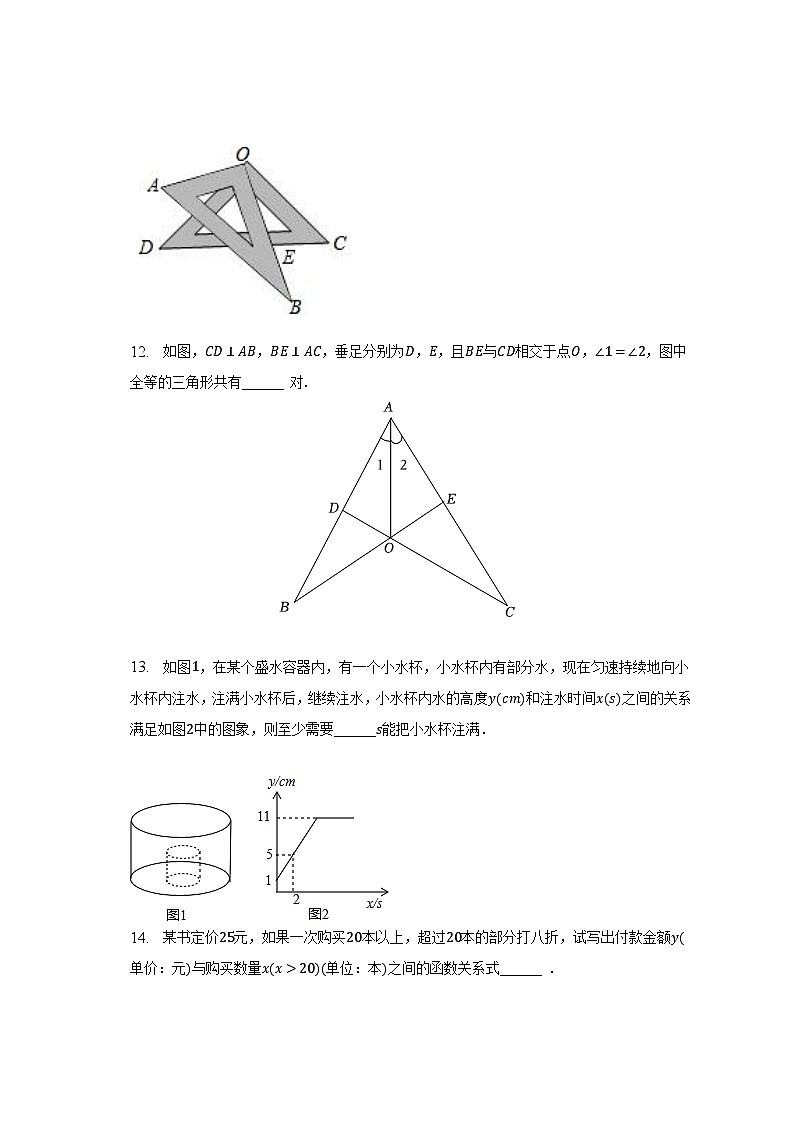
11. 如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB//OC，DC与OB交于点E，则∠DEO的度数为          ．


12. 如图，CD⊥AB，BE⊥AC，垂足分别为D，E，且BE与CD相交于点O，∠1=∠2，图中全等的三角形共有______ 对.

13. 如图1，在某个盛水容器内，有一个小水杯，小水杯内有部分水，现在匀速持续地向小水杯内注水，注满小水杯后，继续注水，小水杯内水的高度y(cm)和注水时间x(s)之间的关系满足如图2中的图象，则至少需要______s能把小水杯注满．


14. 某书定价25元，如果一次购买20本以上，超过20本的部分打八折，试写出付款金额y(单价：元)与购买数量x(x>20)(单位：本)之间的函数关系式______ ．
15. 如图，点D是△ABC三边垂直平分线的交点，若∠A=64°，则∠D=______°.


16. 如图1，一张四边形纸片ABCD，∠A=50°，∠C=150°.若将其按照图2所示方式折叠后，恰好MD′//AB，ND′//BC，则∠D的度数为______ ．

三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题4.0分)
一个缺角的三角形线片如图所示，请你利用尺规画一个与它一样的(全等的三角形.(不写作法，但要保留作图痕迹.)

18. (本小题14.0分)
(1)计算：
①(−3×105)×(7×104)×(−2×103)2；
②(m+n−1)(m−n+1)．
(2)化简求值：[a2+b2−(a−b)2+2b(a−b)]÷4b，其中a=1，b=2．
19. (本小题6.0分)
如图，O为码头，A、B两个灯塔与码头的距离相等，OA，OB为海岸线，一艘轮船离开码头，计划沿∠AOB的平分线OP航行，在航行途中，测得轮船到达P时与灯塔A和灯塔B的距离相等，试问：轮船航行时是否偏离预定航线？请说明理由．

20. (本小题6.0分)
如图，在四边形ABCD中，AB//DC，点E是CD的中点，AE=BE．
求证：∠D=∠C．
证明：∵AB//DC
∴∠EAB=∠DEA
∠EBA=∠CEB(    )
∵AE=BE
∴∠EAB=∠EBA
∴∠ ______ =∠ ______
∵E为CD中点
∴ED=EC
在△ADE和△BCE中
ED=EC∠DEA=AE=BE ______
∴△ADE≌△BCE(    )
∴∠D=∠C(    )

21. (本小题6.0分)
将社团学生分成6组，各组男、女生的人数如下表：
组
第1组
第2组
第3组
第4组
第5组
第6组
男生
6
5
4
5
5
6
女生
5
6
6
5
6
5
从社团选出1名劳动标兵，求下列事件发生的概率．
(1)标兵是第2组的男生；
(2)标兵是第4组的学生；
(3)标兵是女生，
22. (本小题6.0分)
2007年的夏天，湖南省由于持续高温和连日无雨，水库蓄水量普遍下降，如图是某水库的蓄水量V(万立方米)与干旱持续时间t(天)之间的关系图，请根据此图，回答下列问题：
(1)该水库原蓄水量为多少万立方米？持续干旱10天后，水库蓄水量为多少万立方米？
(2)若水库的蓄水量小于400万立方米时，将发出严重干旱警报，请问持续干旱多少天后，将发出严重干旱警报？
(3)按此规律，持续干旱多少天时，水库将干涸？

23. (本小题8.0分)
如图，在△ABC中，AB=AC，作AD⊥AB交BC的延长线于点D，作AE//BD，CE⊥AC，且AE与CE相交于点E．
求证：AD=CE．

24. (本小题10.0分)
(1)计算观察下列各式填空：
第1个：(a−b)(a+b)= ______ ；
第2个：(a−b)(a2+ab+b2)= ______ ；
第3个：(a−b)(a3+a2b+ab2+b3)= ______ ；
这些等式反映出多项式乘法的某种运算规律．
(2)猜想：若n为大于1的正整数，则(a−b)(an−1+an−2b+an−3b²+…+a2bn−3+abn−2+bn−1)= ______ ；
(3)利用(2)的猜想结论计算：2n−1+2n−2+2n−3+…23+22+2+1= ______ ．
(4)扩展与应用：3n−1+3n−2+3n−3+…+33+32+3+1= ______ ．
25. (本小题12.0分)
已知点C为线段AB上一点，分别以AC，BC为边在线段AB同侧作△ACD和△BCE，且CA=CD.CB=CE，∠ACD=∠BCE，直线AE与BD交于点F．
(1)如图1，可得△ACE≌ ______ ；若∠ACD=60°，则∠AFB= ______ ；
(2)如图2，若∠ACD=a，则∠AFB= ______ .(用含a的式子表示)
(3)设∠ACD=a，将图2中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD，AE中的一条线段上)，如图3，试探究∠AFB与a的数量关系，并予以说明．
答案和解析

1.【答案】B 
【解析】解：A、原式=a−b−c，故本选项错误；
B、原式=6a5，故本选项正确；
C、原式=2a3，故本选项错误；
D、原式=x2+2x+1，故本选项错误；
故选：B．
根据去括号，单项式的乘法，合并同类项以及完全平方公式进行解答．
本题考查了单项式乘单项式，整式的加减，完全平方公式，熟记计算法则和完全平方公式即可解题．

2.【答案】D 
【解析】解：A、不是轴对称图形，故此选项错误；
B、不是轴对称图形，故此选项错误；
C、不是轴对称图形，故此选项错误；
D、是轴对称图形，故此选项正确；
故选：D．
根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析．
此题主要考查了轴对称图形，判断轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．

3.【答案】A 
【解析】解：0.001239g/cm3=1.239×10−3g/cm3，
故选：A．
将一个数表示为a×10n的形式，其中1≤|a|