2022-2023学年安徽省合肥市肥西县高二（下）期末数学试卷（含解析）

这是一份2022-2023学年安徽省合肥市肥西县高二（下）期末数学试卷（含解析），共20页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年安徽省合肥市肥西县高二（下）期末数学试卷
一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）
1. 已知集合A={−2,−1,0,1,2}，B={x|(x−1)2≤4}，则A∩B=(    )
A. {−1,0,1} B. {0,1,2} C. {−1,0,1,2} D. {−2,−1,0,1,2}
2. 若复数z=2+ai3−i是纯虚数，则实数a=(    )
A. −6 B. −23 C. 23 D. 6
3. 曲线y=lnxx2+1在点(1,0)处的切线方程为(    )
A. y=12x B. y=12x−12 C. y=34x D. y=34x−34
4. 根据变量x和y的一组试验数据(xi,yi)(i=1,2,…,n)计算可得x−=3，y−=8，回归直线方程为y =b x+1.7，则可以预测当x=13时，变量y的估计值为(    )
A. 29 B. 30 C. 31 D. 32
5. 定义高阶等差数列：对于一个给定的数列{an}，令bn=an+1−an，则数列{bn}称为数列{an}的一阶差数列，再令cn=bn+1−bn，则数列{cn}是数列{an}的二阶差数列.已知数列{An}为2，5，11，21，36，…，且它的二阶差数列是等差数列，则A8=(    )
A. 45 B. 85 C. 121 D. 166
6. 已知等边△ABC的边长为2，DA=2BD，CE=ED，连接BE并延长交AC于F，则AD⋅FA=(    )
A. 14 B. −14 C. 1 D. −1
7. (xy+y−2x−2)6的展开式中x3y5的系数为(    )
A. −240 B. 240 C. −360 D. 360
8. 某校高三男生的身高X(单位：cm)服从正态分布N(170,σ2)，且P(160≤X≤180)=0.6.从该校随机抽取n名高三男生，其中至少有1人身高超过180cm的概率大于0.6，则n的最小值为(    )
A. 4 B. 5 C. 6 D. 7
二、多选题（本大题共4小题，共20.0分。在每小题有多项符合题目要求）
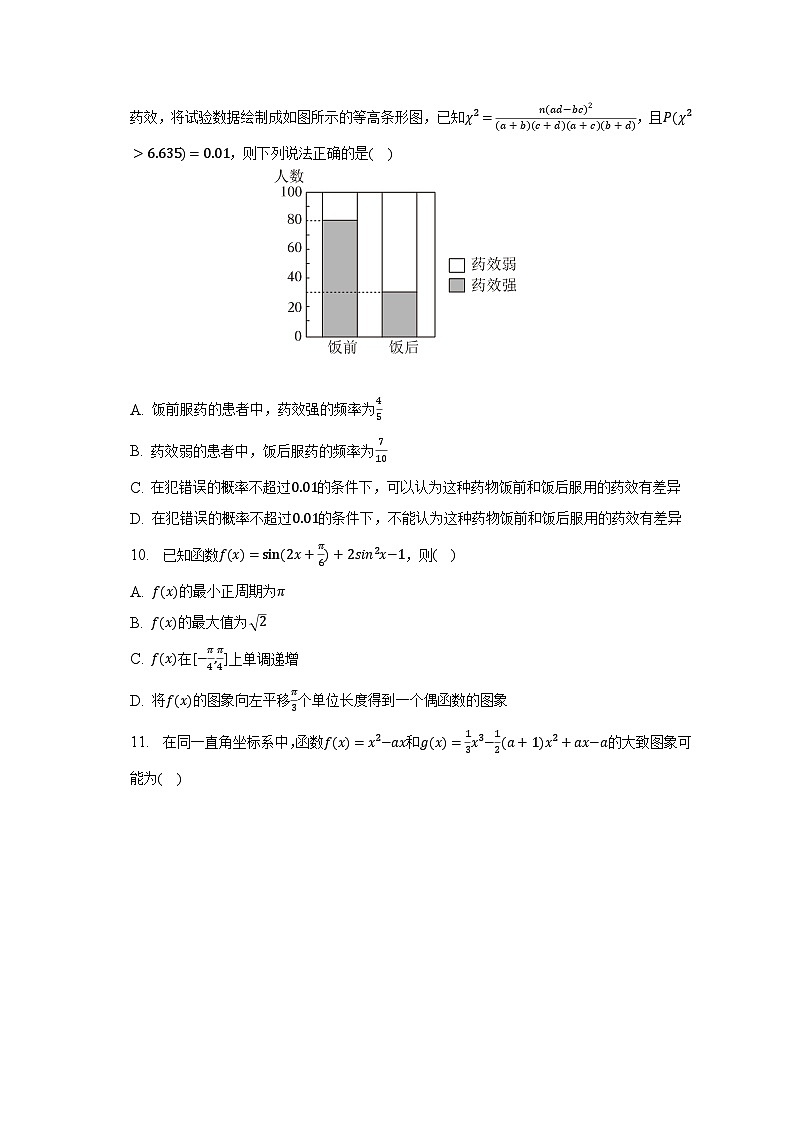
9. 某制药公司为了研究某种治疗高血压的药物在饭前和饭后服用的药效差异，随机抽取了200名高血压患者开展试验，其中100名患者饭前服药，另外100名患者饭后服药，随后观察药效，将试验数据绘制成如图所示的等高条形图，已知χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)，且P(χ2>6.635)=0.01，则下列说法正确的是(    )

A. 饭前服药的患者中，药效强的频率为45
B. 药效弱的患者中，饭后服药的频率为710
C. 在犯错误的概率不超过0.01的条件下，可以认为这种药物饭前和饭后服用的药效有差异
D. 在犯错误的概率不超过0.01的条件下，不能认为这种药物饭前和饭后服用的药效有差异
10. 已知函数f(x)=sin(2x+π6)+2sin2x−1，则(    )
A. f(x)的最小正周期为π
B. f(x)的最大值为 2
C. f(x)在[−π4,π4]上单调递增
D. 将f(x)的图象向左平移π3个单位长度得到一个偶函数的图象
11. 在同一直角坐标系中，函数f(x)=x2−ax和g(x)=13x3−12(a+1)x2+ax−a的大致图象可能为(    )
A. B.
C. D.
12. 已知数列{an}满足a1=35，an+1=3an1+2an(n∈N*)，则(    )
A. 数列{1an−1}为等比数列 B. an<1
C. ∃k∈N*，ak>ak+1 D. 1a1+1a2+…+1an 三、填空题（本大题共4小题，共20.0分）
13. 某电影院有4部科幻电影和2部喜剧电影即将上映，小明准备观看其中的3部，且至少观看1部喜剧电影，则不同的观看方案有______ 种.(用数字填写答案)
14. 记等差数列{an}的前n项和为Sn，已知S13<0，a5+a7>0，则当Sn取最大值时，n的值为______ ．
15. 某工厂的A，B，C车间生产同一产品，产量分别占总产量的20%，30%，50%，且A，B，C车间生产的产品的次品率之比为12：13：15，若该工厂整体的次品率为1.5%，则A车间的次品率为______ ．
16. 若关于x的方程mex=−x2+x+1有三个不等实数根，则实数m的取值范围是______ ．
四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题10.0分)
在△ABC中，角A，B，C所对的边分别为a，b，c，已知−acosA= 3bsinB．
(Ⅰ)求角A；
(Ⅱ)若b2+c2+bc=7，且sinBsinC=314，求△ABC的面积．
18. (本小题12.0分)
已知数列{an}的前n项和Sn=n2+3．
(Ⅰ)求an；
(Ⅱ)设bn=10anan+1，数列{bn}的前n项和为Tn，若Tn 19. (本小题12.0分)
如图，在三棱锥P−ABC中，△PAB是等边三角形，△ABC是等腰直角三角形，AB=BC=2，点P在平面ABC内的射影D恰好落在棱AC上．
(Ⅰ)证明：AC⊥平面PBD；
(Ⅱ)求二面角B−PA−C的余弦值．

20. (本小题12.0分)
某社区居民中青少年、中年人、老年人的人数相同，现按三个年龄段人数比例用分层随机抽样的方法从中抽取60人，调查他们的日均微信步数，统计结果如下：
日均微信步数
[0,4000)
[4000,8000)
[8000,12000)
[12000,16000]
青少年
6
4
x
5
中年人
6
3
7
y
老年人
8
z
4
2
(Ⅰ)求x，y，z的值；
(Ⅱ)从这60人中随机抽取2名日均微信步数在[8000,16000]内的中年人，记这2人中日均微信步数在[12000,16000]内的人数为X，求X的分布列与数学期望；
(Ⅲ)以样本数据中日均微信步数位于各区间的频率作为该社区居民日均微信步数位于该区间的概率，假设该社区的老年人中有30%年龄大于70岁，且年龄大于70岁的老年人中有15%的人日均微信步数在[12000,16000]内，现从该社区任选一名老年人，若已知此老年人的日均微信步数在[12000,16000]内，求他的年龄大于70岁的概率．
21. (本小题12.0分)
已知双曲线E：x2a2−y2b2=1(a>0,b>0)的右焦点为F( 5,0)，过F且斜率为1的直线与E的渐近线分别交于A，B两点(A在第一象限)，O为坐标原点，|OA||OB|=3．
(Ⅰ)求E的方程；
(Ⅱ)过点(4,0)且倾斜角不为0的直线与E交于C，D两点，与E的两条渐近线分别交于P，Q两点，证明：|CP|=|DQ|．
22. (本小题12.0分)
已知函数f(x)=sinx−ax−2(a∈R)．
(Ⅰ)当a=12时，讨论f(x)在区间[0,π2]上的单调性；
(Ⅱ)若当x≥0时，f(x)+ex+cosx≥0，求a的取值范围．
答案和解析

1.【答案】C 
【解析】解：由(x−1)2≤4得−1≤x≤3，∴A∩B={−1,0,1,2}．
故选：C．
先将集合B表示出来，再与集合A找公共元素即可．
本题考查集合的表示与运算，属于基础题．

2.【答案】D 
【解析】解：z=2+ai3−i=(2+ai)(3+i)(3−i)(3+i)=6−a+(2+3a)i10为纯虚数，
则6−a=02+3a≠0，解得a=6．
故选：D．
根据已知条件，结合纯虚数的定义，以及复数的四则运算，即可求解．
本题主要考查复数的四则运算，属于基础题．

3.【答案】B 
【解析】解：由y=lnxx2+1，得y′=1x(x2+1)−2xlnx(x2+1)2=x+1x−2xlnx(x2+1)2，
则y′|x=1=12，
∴曲线y=lnxx2+1在点(1,0)处的切线方程为y=12(x−1)，
即y=12x−12．
故选：B．
求出原函数的导函数，得到函数在x=1处的导数值，再由直线方程的点斜式得答案．
本题考查利用导数研究过曲线上某点处的切线方程，熟记基本初等函数的导函数是关键，是基础题．

4.【答案】A 
【解析】解：x−=3，y−=8，则样本点的中心的坐标为(3,8)，
代入y =b x+1.7，得b =8−1.73=2.1，
∴y =2.1x+1.7，
把x=13代入，可得y =2.1×13+1.7=29．
故选：A．
把已知样本点的中心的坐标代入线性回归方程，求得b ，再求x=13求解y 值即可．
本题考查线性回归方程，明确线性回归方程恒过样本点的中心是关键，是基础题．

5.【答案】C 
【解析】解：该数列的一阶差数列为3，6，10，15，…，
则二阶差数列为3，4，5，…，因为二阶差数列是等差数列，
故二阶差数列后面的项为6，7，8，…，
一阶差数列后面的项为21，28，36，…，
从而原数列后面的项为57，85，121，…，
故A 8=121．
故选：C．
因为二阶差数列是等差数列，由此将原数列一一列举即可．
本题考查等差数列的性质，属于中档题．

6.【答案】D 
【解析】解：设AF=λAC，∵DA=2BD，CE=ED，
∴AD=23AB，
AE=12(AD+AC)=12(23AB+1λAF)=13AB+12λAF，
因为B，E，F三点共线，所以13+12λ=1，解得λ=34，
所以AF=34AC，
因为等边△ABC的边长为2，
故AD⋅FA=23AB⋅(−34AC)=−12AB⋅AC=−12×2×2×12=−1．
故选：D．
根据平面向量基本定理，计算出AF与AC的关系，再利用等边三角形的边长及夹角，即可求得．
本题考查平面向量的线性运算和数量积运算，属基础题．

7.【答案】A 
【解析】解：由于(xy+y−2x−2)6表示6个因式(xy+y−2x−2)的乘积，
展开式中要得到含x3y5的项，需有两个因式取xy，一个因式取−2x，剩下的3个因式取y；
或有三个因式取xy，两个因式取y，剩下的一个因式取−2．
故展开式中x3y5的系数为C62⋅C41⋅(−2)⋅C33+C63⋅C32⋅C11⋅(−2)=−120−120=−240．
故选：A．
由题意，利用乘方的几何意义，组合数公式，计算求得结果．
本题主要考查乘方的几何意义，组合数公式的应用，属于基础题．

8.【答案】B 
【解析】解：某校高三男生的身高X(单位：cm)服从正态分布N(170,σ2)，且P(160≤X≤180)=0.6，
则P(170≤X≤180)=12P(160≤X≤180)=0.3，
故P(X>180)=0.5−0.3=0.2，
由题意可知，1−(1−0.2)n>0.6，即0.8n<0.4，
当n=4时，0.84=0.4096>0.4，
当n=5时，0.85=0.32678<0.4，
故n的最小值为5．
故选：B．
根据已知条件，结合正态分布的对称性，以及对立事件概率和为1，即可求解．
本题主要考查正态分布的对称性，以及对立事件概率和为1，属于基础题．

9.【答案】AC 
【解析】解：由题意可得：在饭前服药的患者中，药效强人有80人，药性弱的有20人；
在饭后服药的患者中，药效强有30人，药性弱的有70人；
所以饭前服药的患者中，药效强的频率为80100=45，故A正确；
药效弱的患者中，饭后服药的频率为7070+20=79，故B错误；
列出2×2联列表得：

 饭前
 饭后
 合计
 药性强
80
 30
 110
 药性弱
 20
 70
 90
 合计
 100
 100
200
所以K2=200(5600−600)2110×90×100×100=500099≈50.51>6.635，
在犯错误的概率不超过0.01的条件下，可以认为这种药物饭前和饭后服用的药效有差异，故C正确，D错误．
故选：AC．
根据等高图，判断A，B；
列出2×2联列表，计算出K2的值，判断C，D．
本题考查了独立性检验、对频率分布直方图(等高图)的认识，属于中档题．

10.【答案】AD 
【解析】解：函数f(x)=sin(2x+π6)+2sin2x−1=sin(2x+π6)−cos2x= 32sin2x+12cos2x−cos2x= 32sin2x−12cos2x=sin(2x−π6)．
对于A：函数的最小正周期为2π2=π，故A正确；
对于B：当2x−π6=2kπ+π2，(k∈Z)时，函数的最大值为1，故B错误；
对于C：由于x∈[−π4,π4]，故2x−π6∈[−2π3,π3]，故函数f(x)在该区间上不单调，故C错误；
对于D：将f(x)的图象向左平移π3个单位长度得到g(x)=sin(2x+2π3−π6)=sin(2x+π2)=cos2x，故该函数为偶函数，故D正确．
故选：AD．
首先利用三角函数关系式的恒等变换，把函数的关系式变形成正弦型函数，进一步利用函数的性质判断A、B、C、D的结论．
本题考查的知识要点：三角函数关系式的恒等变换，正弦型函数的性质，主要考查学生的理解能力和计算能力，属于中档题．

11.【答案】BCD 
【解析】解：根据题意，函数f(x)=x2−ax=x(x−a)，其与x轴的交点为(0,0)、(a,0)，
g(x)=13x3−12(a+1)x2+ax−a，与y轴的交点为(0,−a)，
则g′(x)=x2−(a+1)x+a=(x−a)(x−1)，
g′(x)为开口向上的二次函数，当a≠1时，g′(x)=0有两个零点，即g(x)存在两个极值点，
依次分析选项：
对于A，由f(x)的图象可得a>0，但g(x)的图象与y轴的交点在x轴上方，即−a>0，有a<0，两者矛盾，A错误；
对于B，当a=1时，f(x)=x(x−1)，与x轴的交点为(0,0)，(1,0)，
g(x)=13x3−x2+x−1，与y轴交点为(0,−1)，
g′(x)=(x−1)2≥0，g(x)递增，符合题意，
对于C，当a<0时，f(x)与x轴的交点为(0,0)，(a,0)，
g(x)与y轴交点在x轴上方，g(x)有两个极值点，符合题意；
对于D，当a=0，f(x)=x2，g(x)=13x3−12x2，f(x)、g(x)都经过原点，
g(x)有两个极值点，符合题意．
故选：BCD．
根据题意，先由f(x)、g(x)的解析式，分析f(x)与x轴的交点情况，以及g(x)与y轴的交点，g(x)的单调性等，由此分析选项，综合可得答案．
本题考查函数的图象分析，涉及函数的导数与单调性的关系，属于基础题．

12.【答案】ABD 
【解析】解：依题意，由an+1=3an1+2an两边取倒数，
可得1an+1=1+2an3an=13an+23，
两边同时减去1，
可得1an+1−1=13an+23−1=13⋅(1an−1)，
∵1a1−1=135−1=23，
∴数列{1an−1}是以23为首项，13为公比的等比数列，故选项A正确；
∴1an−1=23⋅(13)n−1=23n，
∴1an=23n+1，
∴an=123n+1=3n3n+2<1，故选项B正确；
∵an+1−an=3n+13n+1+2−3n3n+2
=3n+1(3n+2)−3n(3n+1+2)(3n+1+2)(3n+2)
=4⋅3n(3n+1+2)(3n+2)>0，
∴数列{an}是单调递增数列，
即∀k∈N*，ak ∴1a1+1a2+⋅⋅⋅+1an
=(231+1)+(232+1)+⋅⋅⋅+(23n+1)
=2⋅(131+132+⋅⋅⋅+13n)+n
=2⋅131−13n+11−13+n
=n+1−13n 故选：ABD．
先将题干中递推公式取倒数，再两边同时减去1，进一步推导即可发现数列{1an−1}是以23为首项，13为公比的等比数列，即可判断选项A的正确性，通过计算数列{1an−1}的通项公式推导数列{1an}的通项公式，进一步计算出数列{an}的通项公式，根据不等式的性质即可判断an与1的大小关系，判断选项B的正确性，然后运用作差法判断数列{an}的单调性，进一步判断选项C的正确性，最后运用分组求和法与等差数列与等比数列的求和公式即可计算出1a1+1a2+⋅⋅⋅+1an的结果，最后根据不等式的性质即可判断选项D的正确性．
本题主要考查数列由递推公式推导出通项公式，以及数列求和与不等式的综合问题．考查了整体思想，转化与化归思想，作差法，分组求和法，等差数列与等比数列求和公式的运用，不等式的性质运用，以及逻辑推理能力和数学运算能力，属中档题．

13.【答案】16 
【解析】解：当只观看1部喜剧电影时，有C21C42=2×6=12种观看方案，
当观看2部喜剧电影时，有C22C41=1×4=4种观看方案，
则不同的观看方案有12+4=16种．
故答案为：16．
分只观看1部喜剧电影和观看2部喜剧电影讨论，即可得出答案．
本题考查排列组合，考查运算求解能力，属于基础题．

14.【答案】6 
【解析】解：因为等差数列{an}中，S13=13(a1+a13)2=13a7<0，a5+a7=2a6>0，
所以a7<0，a6>0，
则当Sn取最大值时，n=6．
故答案为：6．
由已知结合等差数列的求和公式及性质可得a7<0，a6>0，从而可求．
本题主要考查了等差数列的求和公式及性质的应用，属于基础题．

15.【答案】2.5% 
【解析】解：设A车间的次品率为12n，则B车间的次品率为13n，C车间的次品率为15n，
则0.2×12n+0.3×13n+0.5×15n=0.015，
解得n=120，
∴A车间的次品率为12×120×100%=2.5%．
故答案为：2.5%．
设A车间的次品率为12n，则B车间的次品率为13n，C车间的次品率为15n，由题意可得0.2×12n+0.3×13n+0.5×15n=0.015，求出n的值，进而求出A车间的次品率．
本题主要考查了全概率公式，属于基础题．

16.【答案】(−5e−2,0) 
【解析】解：令f(x)=ex(−x2+x+1)，x∈R，
由题意可得y=m与y=f(x)有三个不同交点，
因为f′(x)=ex(−x2+x+1)+ex(−2x+1)=ex(−x2−x+2)，
令f′(x)=0，则有−x2−x+2=0，
解得x1=−2，x2=1，
所以当x∈(−∞,−2)时，f′(x)<0，f(x)单调递减；
当x∈(−2,1)时，f′(x)>0，f(x)单调递增；
当x∈(1,+∞)时，f′(x)<0，f(x)单调递减；
所以f(x)极小值=f(−2)=−5e−2，f(x)极大值=f(1)=e，
令f(x)=ex(−x2+x+1)=0，
解得x3=1− 52，x4=1+ 52，
所以当x<1− 52时，f(x)<0；
当1− 520，
当x>1+ 52时，f(x)<0，
作出f(x)的图象，如图所示：

又因为y=m与y=f(x)有三个不同交点，
所以m∈(−5e−2,0)．
故答案为：(−5e−2,0)．
令f(x)=ex(−x2+x+1)，x∈R，将问题转化为y=m与y=f(x)有三个不同交点，利用导数确定函数的单调性，求出极值，作出f(x)的图象，结合图象即可得答案．
本题考查了转化思想、数形结合思想及导数的综合运用，作出图象是关键，属于中档题．

17.【答案】解：(Ⅰ)因为−acosA= 3bsinB，
由正弦定理得−sinAsinB= 3sinBcosA，
因为sinB>0，
所以sinA=− 3cosA，即tanA=− 3，
所以A=120°；
(Ⅱ)由余弦定理得cosA=−12=b2+c2−a22bc，
所以b2+c2−a2=−bc，
因为b2+c2+bc=7，
所以a= 7，
由正弦定理得bsinB=csinC=asinA= 7 32=2 213，
所以bc=2 213sinB×2 213sinC=2，
故△ABC的面积S=12bcsinA=12×2× 32= 32． 
【解析】(Ⅰ)由已知结合正弦定理及同角基本关系可求tanA，进而可求A；
(Ⅱ)由已知结合余弦定理可求a，然后结合正弦定理可求bc，再由三角形面积公式可求．
本题主要考查了正弦定理，余弦定理及三角形面积公式的应用，属于中档题．

18.【答案】解：(Ⅰ)∵Sn=n2+3①，
∴当n=1时，a1=S1=4，
当n≥2时，Sn−1=(n−1)2+3②，
∴由①−②得an=2n−1，
当n=1时，a1=4不符合上式，
∴an=4,n=12n−1,n≥2；
(Ⅱ)由(Ⅰ)得an=4,n=12n−1,n≥2，
∴当n=1时，b1=10a1a2=104×3=56，
当n≥2时，bn=10anan+1=10×12(12n−1−12n+1)=5(12n−1−12n+1)，
∴当n≥2时，Tn=b1+b2+...+bn=56+5[(13−15)+(15−17)+...+(12n−1−12n+1)]
=56+5(13−12n+1)=52−52n+1<52，
又T1=b1<52，
故Tn ∴m的最小整数值为3． 
【解析】(Ⅰ)由题意得当n=1时，a1=S1=4，当n≥2时，Sn−1=(n−1)2+3，作差变形得an=2n−1，验证n=1，即可得出答案；
(Ⅱ)由(Ⅰ)得an=4,n=12n−1,n≥2，分类讨论n=1，n≥2，利用裂项法求和，即可得出答案．
本题考查数列的递推式和数列的求和，考查转化思想，考查逻辑推理能力和运算能力，属于中档题．

19.【答案】解：(Ⅰ)证明：取AB的中点E，连接PE，DE，
由题意知PD⊥平面ABC，AB⊂平面ABC，
∴PD⊥AB，
∵△PAB是等边三角形，E是AB的中点，
∴PE⊥AB，
又PE∩PD=P，
∴AB⊥平面PDE，
∴AB⊥DE，
在等腰直角△ABC中，AB=BC，∴AB⊥BC，
∴BC//DE，
又∵E是AB的中点，∴D是AC的中点，
∴BD⊥AC，
又∵PD⊥AC，PD∩BD=D，
∴AC⊥平面PBD；
(Ⅱ)由题意建立以D为坐标原点，DE，DP所在直线分别为x，z轴的空间直角坐标系，如图所示：

由题意得PE= 3，DE=1，则PD= PE2−DE2= 2，
则D(0,0,0)，A(1,1,0)，B(1,−1,0)，P(0,0, 2)，
∴PA=(1,1,− 2)，AB=(0,−2,0)，
设平面PAB的法向量为n=(x,y,z)，
则PA⋅n=x+y− 2z=0AB⋅n=−2y=0，取z=1，则x= 2，y=0，
∴平面PAB的法向量为n=( 2,0,1)，
又平面PAC的一个法向量为DB=(1,−1,0)，
∴cos=DB⋅n|DB|⋅|n|= 2 2× 3= 33，
∴二面角B−PA−C的余弦值为 33． 
【解析】(Ⅰ)取AB的中点E，连接PE，DE，利用线面垂直的判定定理，即可证明结论；
(Ⅱ)由题意建立以D为坐标原点，DE，DP所在直线分别为x，z轴的空间直角坐标系，求出法向量，利用向量法，即可得出答案．
本题考查直线与平面垂直和二面角，考查转化思想，考查逻辑推理能力和运算能力，属于中档题．

20.【答案】解：(I)由题意，得6+4+x+5=206+3+7+y=208+z+4+2=20，解得x=5y=4z=6；
(Ⅱ)由(Ⅰ)可知，日均微信步数在[8000,16000]内的中年人有11人，在[12000,16000]内的中年人有4人，
则X的所有可能取值为0，1，2，
P(X=0)=C72C112=2155,P(X=1)=C71C41C112=2855,P(X=2)=C42C112=655，
所以X的概率分布列：
 X
 0
 1
 2
 P
 2155
 2855
 655
所以 E(X)=0×2155+1×2855+2×655=811；
(Ⅲ)设A表示事件“该社区老年人的日均微信步数在[12000,16000]内”，B表示事件“该社区老年人的年龄大于70岁”，
由题知，P(A)=220=0.1，
P(AB)=30%×15%=0.045，
则P(B|A)=P(AB)P(A)=0.0450.1=0.45=920． 
【解析】(Ⅰ)由题意得6+4+x+5=206+3+7+y=208+z+4+2=20，即可求解；
(Ⅱ)由(Ⅰ)可知，日均微信步数在[8000,16000]内的中年人有11人，在[12000,16000]内的中年人有4人，则X的所有可能取值为0，1，2，计算出各自对应的概率即可求解；
(Ⅲ)设A表示事件“该社区老年人的日均微信步数在[12000,16000]内”，B表示事件“该社区老年人的年龄大于70岁”，利用条件概率公式即可求解．
本题考查统计表，随机变量的分布列与期望，属于中档题．

21.【答案】解：(Ⅰ)已知双曲线E的右焦点为F( 5,0)，
所以c= 5，①
又过F且斜率为1的直线与E的渐近线分别交于A，B两点，
此时直线l的方程为y=x− 5，
联立y=x− 5y=bax，
解得yA= 5ba−b，
同理，得yB=− 5ba+b，
因为|OA||OB|=3，
整理得 5ba−b=3 5ba+b，
解得a=2b，②
又a2+b2=c2，③
联立①②③，解得a=2，b=1，
所以E的方程为x24−y2=1；
(Ⅱ)证明：因为过点(4,0)且倾斜角不为0的直线与E交于C，D两点，与E的两条渐近线分别交于P，Q两点，
要证|CP|=|DQ|，
即证CD的中点与PQ的中点重合，
不妨设CD的中点为M，直线CD的方程为x=my+4，
联立x=my+4x24−y2=1，消去x并整理得(m2−4)y2+8my+12=0，
设C(x1,y1)，D(x2,y2)，
由韦达定理得y1+y2=8m4−m2，
而yM=y1+y22=4m4−m2，xM=m(4m4−m2)+4=164−m2，
即M(164−m2,4m4−m2)，
联立x=my+4y=12x，解得x=82−my=42−m，
所以P(82−m,42−m)，
联立x=my+4y=−12x，解得x=82+my=−42+m，
所以Q(82+m,−42+m)，
可得PQ的中点N(164−m2,4m4−m2)，
因为点M与点N重合，
所以|CP|=|DQ|． 
【解析】(Ⅰ)由题意，得到直线l的方程，将直线l的方程与渐近线方程联立，求出点A，B的纵坐标，根据|OA||OB|=3，列出等式得到a=2b，结合双曲焦点坐标以及a2+b2=c2，列出等式即可求出双曲线的方程；
(Ⅱ)将求证|CP|=|DQ|，转化成求证CD的中点与PQ的中点重合，设CD的中点为M，直线CD的方程为x=my+4，将直线CD的方程与双曲线方程联立，设出点C，D的坐标，结合韦达定理得到点M的坐标；将直线CD的方程与双曲线渐近线方程联立，求出点N的坐标，进而即可得证．
本题考查双曲线的性质以及直线与圆锥曲线的综合问题，考查了逻辑推理、转化思想和运算能力．

22.【答案】解：(Ⅰ)由题意得f(x)=sinx−12x−2，x∈[0,π2]，则f′(x)=cosx−12，
由f′(x)=0得x=π3，由f′(x)>0得0≤x<π3，由f′(x)<0得π3 ∴f(x)在[0,π3]上单调递增，在[π3,π2]上单调递减；
(Ⅱ)当x≥0时，f(x)+ex+cosx≥0，令h(x)=sinx−ax−2+ex+cosx，
题意转化为当x≥0时，h(x)≥0，
则h′(x)=ex+cosx−sinx−a，
令t(x)=ex+cosx−sinx−a，则t′(x)=ex−sinx−cosx，
又y=ex−x−1，y′=ex−1，
由y′=0得x=0，由y′>0得x>0，由y′<0得x<0，
∴y=ex−x−1在(−∞,0)上单调递减，在(0,+∞)上单调递增，
∴当x=0时，y取得最小值也是极小值，即ex−x−1≥0，
∴ex≥x+1恒成立，
令y=x−sinx，y′=1−sinx≥0，
∴y=x−sinx在[0,+∞)上单调递增，即x≥sinx在[0,+∞)上恒成立，
∴当x≥0时，t′(x)=ex−sinx−cosx≥x+1−x−cosx=1−cosx≥0，
∴t(x)=ex+cosx−sinx−a在[0,+∞)上单调递增，
∴当x≥0时，t(x)min=t(0)=2−a，且当x→+∞时，t(x)→+∞，
∴当a≤2时，h′(x)=t(x)≥0，即h(x)在[0,+∞)上单调递增，
此时对于∀x∈[0,+∞)，h(x)≥h(0)=0符合题意；
当a>2时，则∃x0∈[0,+∞)，使得t(x0)=0，即h′(x0)=0，
∴当0 此时h(x) 综上所述，a的取值范围为(−∞,2]． 
【解析】(Ⅰ)由题意得f(x)=sinx−12x−2，x∈[0,π2]，则f′(x)=cosx−12，求出f′(x)>0，f′(x)<0，即可得出答案；
(Ⅱ)构造函数h(x)=sinx−ax−2+ex+cosx，题意转化为当x≥0时，h(x)≥0，求出h′(x)，利用导数研究函数的单调性，求出最小值，即可得出答案．
本题考查利用导数研究函数的单调性和最值，考查转化思想和函数思想，考查逻辑推理能力和运算能力，属于中档题．