中考数学复习章节限时练5四边形含答案

这是一份中考数学复习章节限时练5四边形含答案，共4页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
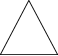
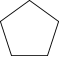
  章节限时练5　四边形(时间：45分钟　　满分：100分)一、选择题(本大题共7小题，每小题6分，共42分)1．下列多边形中，内角和最大的是                     (  D  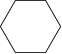)                      A             B            C               D2．如图，▱ABCD的周长为20，对角线AC，BD交于点O，点E为CD的中点，BD＝6，则△DOE的周长为                     （  B  ）A．5        B．8   C．10       D．12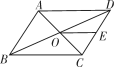 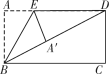   　　　　　第2题图                   第4题图3．(2021·泸州)下列命题中是真命题的是                 (  B  )A．对角线相等的四边形是平行四边形B．对角线互相平分且相等的四边形是矩形C．对角线互相垂直的四边形是菱形D．对角线互相垂直平分的四边形是正方形4．如图，将矩形纸片ABCD沿BE折叠，使点A落在对角线BD上的点A′处．若∠DBC＝24°，则∠A′EB的度数为               （  C  ）A．66°  B．60°  C．57°  D．48°5．(2021·常德)如图，已知F，E分别是正方形ABCD的边AB与BC的中点，AE与DF交于点P，则下列结论中成立的是          (  C   )A．BE＝AE  　　           B．PC＝PDC．∠EAF＋∠AFD＝90°  　　D．PE＝EC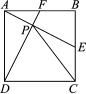 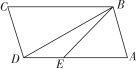       　　　第5题图                   第6题图6．★(2022·无锡)如图，在▱ABCD中，AD＝BD，∠ADC＝105°，点E在AD上，∠EBA＝60°，则的值是                    （  D  ）A.  B.  C.  D.7．★如图，在菱形ABCD中，∠A＝60°，点E，F分别在边AB，BC上， AE＝BF＝2，△DEF的周长为3 ，则AD的长为      （  C  ）A.             B．2   C.＋1          D．2 －1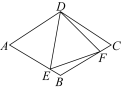　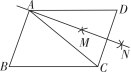         　　第7题图                     第9题图二、填空题(本大题共3小题，每小题6分，共18分)8．在矩形ABCD中，点E，F分别在BC，AD上，AF＝EC.只需添加一个条件即可证明四边形AECF是菱形，这个条件可以是AE＝AF(答案不唯一)．(写出一个即可)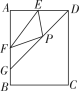9．(2022·盘锦)如图，四边形ABCD为平行四边形，AB＝2，BC＝3.按以下步骤作图：①分别以点C和点D为圆心，大于CD的长为半径作弧，两弧交于M，N两点；②作直线MN.若直线MN恰好经过点A，则▱ABCD的面积是4 .10．★(2022·贺州)如图，在矩形ABCD中，AB＝8，BC＝6，E，F分别是AD，AB的中点，∠ADC的平分线交AB于点G，点P是线段DG上的一个动点，则△PEF的周长最小值为5＋.三、解答题(本大题共2小题，共40分)11．(14分)如图，在菱形ABCD中，∠B＝38°.(1)在AB边上求作一点P，使PB＝PC(要求：尺规作图，保留作图痕迹，不写作法)；(2)在(1)的条件下，连接AC，求∠ACP的度数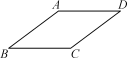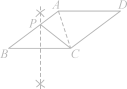．       题图                 答图  解：(1)如答图，点P即为所求．(2)∵四边形ABCD为菱形，∴BA＝BC.∴∠BAC＝∠BCA＝(180°－∠B)＝×(180°－38°)＝71°.∵PB＝PC，∴∠PCB＝∠B＝38°，∴∠ACP＝∠BCA－∠PCB＝71°－38°＝33°. 12．(26分)在▱ABCD中，BE平分∠ABC交AD于点E.(1)如图①，若∠D＝30°，AB＝，求△ABE的面积；(2)如图②，过点A作AF⊥DC，交DC的延长线于点F，分别交BE，BC于点G，H，且AB＝AF.求证：ED－AG＝FC.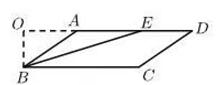 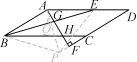   　     ①                        ②(1)解：过点B作BO⊥AD交DA延长线于点O，如图①所示，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AB＝CD，∠ABC＝∠D＝30°，∴∠BAO＝∠D＝30°，∴BO＝AB＝.∵BE平分∠ABC，∴∠ABE＝∠CBE，∴∠ABE＝∠AEB，∴AE＝AB＝，∴S△ABE＝AE·BO＝.(2)证明：作AQ⊥BE交DF的延长线于点P，垂足为点Q，连接PB，PE，如图②所示，∵AB＝AE，AQ⊥BE，∴∠ABE＝∠AEB，BQ＝EQ，∴PB＝PE，∴∠PBE＝∠PEB，∴∠ABP＝∠AEP.∵AB∥CD，AF⊥CD，∴AF⊥AB，∴∠BAF＝90°.∵AQ⊥BE，∴∠ABG＝∠FAP，∵AB＝AF，∴△ABG≌△FAP(ASA)，∴AG＝FP.∵AB∥CD，AD∥BC，∴∠ABP＋∠BPC＝180°，∠BCP＝∠D，∵∠AEP＋∠PED＝180°，∴∠BPC＝∠PED，∴△BPC≌△PED(AAS)，∴PC＝ED，∴ED－AG＝PC－AG＝PC－FP＝FC.