中考数学复习压轴解答题题组练一含答案

这是一份中考数学复习压轴解答题题组练一含答案，共6页。
  压轴解答题题组练一(针对中考：解答题第24—25题)(时间：45分钟　　满分：20分)　　　　　　　　　　　　　　　1．(10分)如图①，抛物线y＝ax2＋bx＋4交x轴于A(－2，0)，B(4，0)两点，与y轴交于点C，连接AC，BC.(1)求此抛物线的解析式；(2)P是抛物线上位于直线BC上方的一个动点，过点P作PQ∥y轴交BC于点Q；过点 P 作PE⊥BC于点E，过点E作EF⊥y轴于点F，求出2PQ＋EF的最大值及此时点P的坐标；(3)如图②，将抛物线y＝ax2＋bx＋4沿着射线CB的方向平移，使得新抛物线y′过点(3，1)，点D为原抛物线y与新抛物线y′的交点，若点G为原抛物线的对称轴上一动点，点H为新抛物线y′上一动点，直接写出所有使得以A，D，G，H为顶点的四边形为平行四边形的点H的坐标，并把求其中一个点H的坐标的过程写出来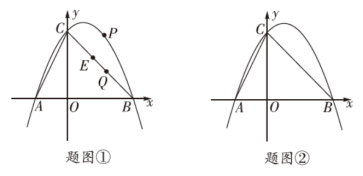．解：(1)此抛物线的解析式为y＝－x2＋x＋4.(2)如答图①，延长FE交PQ于点G，则FG⊥PQ，∵抛物线y＝－x2＋x＋4与y轴交于点C，∴C(0，4)，∵B(4，0)，∴OB＝OC＝4，∵∠BOC＝90°，∴△BOC是等腰直角三角形，∠CBO＝∠BCO＝45°，∵B(4，0)，C(0，4)，∴直线BC的解析式为y＝－x＋4，∵点P在抛物线上，PQ∥y轴交BC于点Q，∴设P，则Q(m，－m＋4)，其中 0＜m＜4，∴PQ＝－m2＋m＋4－(－m＋4)＝－m2＋2m，∵PE⊥BC，PQ∥y轴，∴∠PEQ＝90°，∠PQE＝∠BCO＝45°，∴△PEQ是等腰直角三角形，∵EG⊥PQ，∴EG＝PQ＝－m2＋m，∴EF＝FG－EG＝m－＝m2，∴2PQ＋EF＝－＋，∵－＜0，∴当m＝时，2PQ＋EF的最大值为，此时点P的坐标为.(3)如答图②，∵B(4，0)，C(0，4)，y＝－(x－1)2＋，∴将抛物线y＝－x2＋x＋4沿着射线CB的方向平移，即向右平移t个单位长度，向下平移t个单位长度，∴平移后的新抛物线解析式为y＝－(x－1－t)2＋－t，∵新抛物线y′过点(3，1)，∴1＝－(3－1－t)2＋－t，解得t＝－1(不符合题意，舍去)或t＝3，∴新抛物线的解析式为y＝－(x－4)2＋＝－x2＋4x－，由得∴D，∵点G为原抛物线的对称轴上一动点，点H为新抛物线y′上一动点，∴设G(1，s)，H，而A(－2，0)，①以 AH，DG为对角线时，则解得r＝，∴－r2＋4r－＝－，∴H；②以AG，DH为对角线时，则解得r＝－，∴－r2＋4r－＝－，∴H；③以AD，GH为对角线时，则·299B·解得r＝，∴－r2＋4r－＝－，∴H；综上所述，点H的坐标为，或. 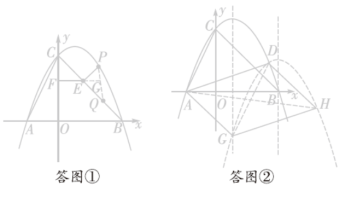2．(10分)如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D是BC边上一动点，连接AD，把AD绕点A逆时针旋转90°，得到AE，连接CE，DE.点F是DE的中点，连接CF.(1)求证：CF＝AD；(2)如图②所示，在点D运动的过程中，当BD＝2CD时，分别延长CF，BA，相交于点G，猜想AG与BC存在的数量关系，并证明你猜想的结论；(3)在点D运动的过程中，在线段AD上存在一点P，使PA＋PB＋PC的值最小．当PA＋PB＋PC的值取得最小值时，AP的长为m，请直接用含m的式子表示CE的长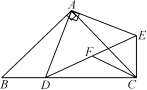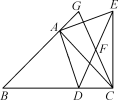．          　   题图①                      题图②(1)证明：∵∠BAC＝∠DAE，∴∠BAD＝∠CAE.∴△ABD≌△ACE(SAS)，∴∠ABD＝∠ACE.∵AB＝AC，∠BAC＝90°，∴∠ABD＝∠ACB＝45°.∴∠ECD＝∠ACB＋∠ACE＝90°.∵F是DE的中点，∴CF＝DE.∵AD＝AE，∠DAE＝90°，∴DE＝AD.∴CF＝AD.(2)解：＝3.证明：如答图①所示，连接AF，DG，DG交AC于点M.由(1)知，AF＝CF＝DF＝DE.∴∠FAC＝∠FCA.∵∠GAC＝90°，∴∠FAG＝∠FGA.∴AF＝GF，∴GF＝DF＝CF，∴∠FGD＝∠FDG，∠FDC＝∠FCD，∴∠FDG＋∠FDC＝90°，∴∠GDC＝90°.∵∠B＝∠ACD＝45°，∴BD＝GD，CD＝MD，∠AMG＝45°.∵∠CAG＝90°，∴MG＝AG.∵BD＝2CD，∴BD＝DG＝2CD＝2MG.∴BC＝3MG＝3AG.即＝3.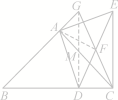 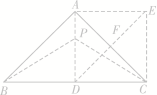         答图①                 答图②(3)解：如答图②所示，当AD⊥BC时，在AD上存在点P，满足条件．此时CE的长为m.