中考数学复习压轴解答题题组练三含答案

  压轴解答题题组练三

(针对中考：解答题第24—25题)

(时间：45分钟　　满分：20分)　　　　　　　　　　　　　　　

1．(10分)如图①，在平面直角坐标系中，抛物线C1：y＝－x2＋bx＋c的图象与坐标轴交于A，B，C三点，其中点A的坐标为(0，8)，点B的坐标为(－4，0)，点D的坐标为(0，4)．

(1)求该二次函数的解析式及点C的坐标；

(2)若点F为该抛物线在第一象限内的一动点，求△FCD面积的最大值；

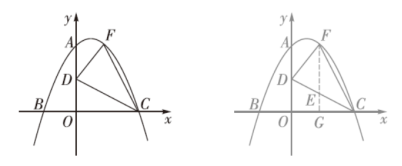
  题图①                  答图①

解：(1)把A(0，8)，B(－4，0)代入y＝－x2＋bx＋c，得解得

∴该二次函数的解析式为y＝－x2＋x＋8；

当y＝0时，得x1＝－4，x2＝8，∴C(8，0)．

(2)如答图①，作FG⊥x轴于点G，交CD于点E.

设直线CD的函数解析式为y＝kx＋4，

则8k＋4＝0，解得k＝－，∴y＝－x＋4.

设F，则E，

∴EF＝－x2＋x＋8＋x－4＝－x2＋x＋4，

∵S△FCD＝OG·EF＋CG·EF＝OC·EF，

∴S△FCD＝×8＝－(x－3)2＋25，

∴当x＝3时，△FCD面积的最大值为25.

(3)如图②，将抛物线C1向右平移2个单位长度，向下平移5个单位长度得到抛物线C2，M为抛物线C2上一动点，N为平面内一动点，问是否存在这样的点M，N，使得四边形DMCN为菱形，若存在，求点N的坐标；若不存在，请说明理由．

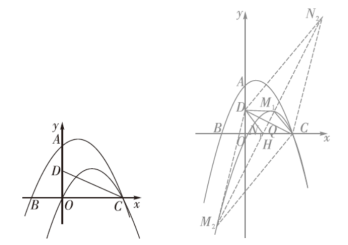
题图②        答图②

解：存在．由题意可知，平移后得抛物线C2：

y＝－(x－4)2＋4＝－x2＋2x.

如答图②，设CD的中点为Q，则Q(4，2)，

过点Q作CD的垂线交抛物线C2于点M，交x轴于点H.

∵∠CQH＝∠COD＝90°，∴＝＝cos∠OCD.

∵OD＝4，CO＝8，∴CD＝4，∴CQ＝2，

∴CH＝＝5，∴OH＝3，H(3，0)，

由点Q(4，2)，H(3，0)求得直线QH的函数解析式为y＝2x－6，

联立

求得M1(2，4－6)，M2(－2，－4－6)，

∵点N与点M关于点Q(4，2)成中心对称，

∴N1(8－2，10－4)，N2(8＋2，10＋4)．

2．(10分)如图，在Rt△ABC中，AC＝BC，∠C＝90°，点D为直线AC上一点，连接BD，将BD绕点B逆时针旋转90°至BE，连接AE交直线BC于点F.

(1)如图①，若BD平分∠ABC，AC＝3，求AD的长；

(2)如图②，求证：AF＝EF；

(3)如图③，当CD＝CF＝AC＝2时，M为直线AB上一动点，连接FM，将△EFB沿直线FM翻折到△EFB同一平面得△E′FB′，当线段CE′最小时，直接写出△DB′E′的面积．

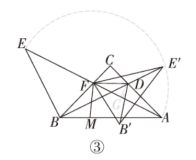
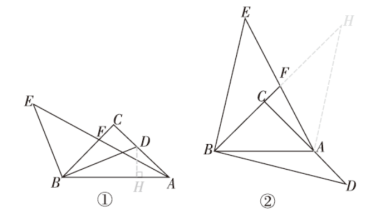
(1)解：如图①中，过点D作DH⊥AB于点H.

∵AC＝BC，∠C＝90°，AC＝3，

∴AB＝ ＝ ＝ 3 ，

∵BD平分∠ABC，∴∠ABD＝∠CBD，

在△DBC和△DBH中，

∴△DBC≌△DBH(AAS)，

∴BH＝BC＝3，∴AH＝AB－BH＝ 3 －3，

∵∠DAH＝45°，∴AD＝ AH＝6－ 3 .

(2)证明：过点A作AH∥BE交BC的延长线于点H.

∴∠H＝∠EBF，∠E＝∠HAF，

∵∠DBE＝90°，∠ACB＝90°，

∴∠D＋∠CBD＝90°，∠EBF＋∠FBD＝90°，

∴∠D＝∠EBF，∴∠D＝∠H，

∵∠BCD＝∠ACH＝90°，CB＝CA，

∴△BCD≌△ACH(AAS)，∴AH＝BD，

∵BD＝BE，∴AH＝BE，∵∠H＝∠EBF，∠E＝∠HAF，

∴△BFE≌△HFA(AAS)，∴AF＝EF.

(3)解：∵CD＝CF＝AC＝2，∴AC＝6，

∴AD＝FB＝4，

∴AF＝ ＝＝ 2，

同理可得EF＝AF＝ 2，∴E′F＝ 2，

∴E′的轨迹是以点F为圆心，E′F＝ 2为半径的圆弧，

∴CE′最小时，F，C，E′共线，

此时∠E′FB′＝∠EFB，∴B′在AE上，

过点D作DG⊥AF于点G，

∵AD·CF＝AF·DG，

∴DG＝＝，

∴S△DFE′＝FB′·DG＝FB·DG

  ＝×4×＝，

∴S△DFE′＝FE′·DC＝× 2　×2＝ 2　，

∵EF＝AF，∴S△BFE＝S△BFA＝BF·AC＝12，

∴S△FB′E′＝12，

∴S△DB′E′＝S△FB′E′－S△DE′F－S△DFB′

＝12－－ 2

＝12－.