中考数学复习压轴解答题题组练五含答案

  压轴解答题题组练五

(针对中考：解答题第24—25题)

(时间：45分钟　　满分：20分)

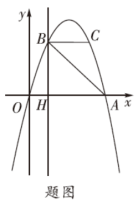
1．(10分)如图，抛物线y＝ax2＋bx过A(4，0)，B(1，3)两点，点C，B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H.

(1)求抛物线的解析式；

(2)点P是抛物线上一动点，且位于第四象限，当△ABP的面积为6时，求出点P的坐标；

(3)若点M在直线BH上运动，点N在x轴上运动，当以点C，M，N为顶点的三角形为等腰直角三角形时，求此时△CMN的面积．

解：(1)由点A(4，0)，B(1，3)求得抛物线解析式为y＝－x2＋4x.

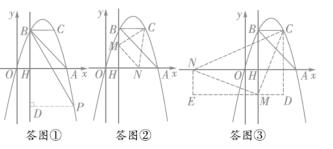
(2)过点P作PD⊥BH交BH于点D，如答图①，设点P(m，－m2＋4m)，BH＝AH＝3，HD＝m2－4m，PD＝m－1，

∵S△ABP＝S△ABH＋S四边形HAPD－S△BPD，

∴×3×3＋(3＋m－1)(m2－4m)－(m－1)·(3＋m2－4m)＝6，整理得3m2－15m＝0，

·303A·解得m1＝0(舍去)，m2＝5，∴点P的坐标为(5，－5)．

(3)∵抛物线的对称轴为直线x＝2，而点C，B关于抛物线的对称轴对称，∴C(3，3)，

以点C，M，N为顶点的三角形为等腰直角三角形时，分以下几类情况讨论：

Ⅰ)以点M为直角顶点且点M在x轴上方时，如答图②，CM＝MN，∠CMN＝90°，

易证得△CBM≌△MHN，

∴BC＝MH＝2，BM＝HN＝3－2＝1，

∴MC＝＝，

∴S△CMN＝××＝；

Ⅱ)以点M为直角顶点且点M在x轴下方时，如答图③，过点M作DE⊥y轴，作NE⊥DE于点E，CD⊥DE于点D，易得Rt△NEM≌Rt△MDC，

∴NE＝MD＝BC＝2，EM＝CD＝BM＝5，

∴CM＝＝，

∴S△CMN＝××＝；

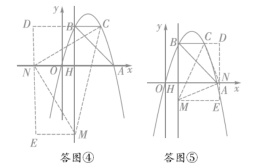
Ⅲ)以点N为直角顶点且点N在y轴左侧时，如答图④，CN＝MN，∠MNC＝90°，易得Rt△NEM≌Rt△CDN，

∴EM＝DN＝BH＝3，

NE＝CD＝BD＋BC＝EM＋BC＝5，

∴CN＝＝，

∴S△CMN＝××＝17；

Ⅳ)以点N为直角顶点且点N在y轴右侧时，如答图⑤，易得Rt△NEM≌Rt△CDN，

∴EM＝DN＝BH＝3，

NE＝CD＝BD－BC＝EM－BC＝1，

∴CN＝＝，

∴S△CMN＝××＝5；

Ⅴ)以点C为直角顶点时，不能构成满足条件的等腰直角三角形，

综上所述，△CMN的面积为，，17或5.

2．(10分)在等腰直角三角形ABC中，∠ABC＝90°，AB＝BC，将线段BC绕点B顺时针旋转一定的角度得到线段BD.连接AD，交BC于点E，过点C作线段AD的垂线，垂足为点F，交BD于点G.

(1)如图①，若∠CBD＝45°.

①求∠BCG的度数；

②连接EG，求证：AE－FG＝EG＋DF；

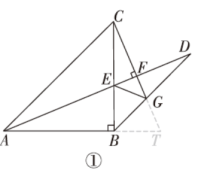
①解：∵BA＝BC，

∠ABC＝90°，

∴∠ACB＝∠CAB＝45°，

∵∠CBD＝45°，

∴∠ACB＝∠CBD，

∴AC∥BD，∴∠CAD＝∠D，

∵BD＝BC＝BA，∴∠D＝∠BAD，

∴∠CAD＝∠BAD＝22.5°，

∵CG⊥AD，∴∠CFD＝90°，

∴∠ACF＝90°－22.5°＝67.5°，

∴∠BCG＝∠ACF－∠ACB＝22.5°.

②证明：延长CG交AB的延长线于点T.

∵∠ABE＝∠CBT＝90°，AB＝BC，

∠BAE＝∠BCT＝22.5°，

∴△ABE≌△CBT(ASA)，

∴AE＝CT，BE＝BT，

∵∠EBG＝∠TBG＝45°，BG＝BG，

∴△BGE≌△BGT(SAS)，

∴EG＝GT，∠T＝∠BEG＝67.5°，

∴∠BGE＝∠BEG＝∠T＝∠BGT＝67.5°，

∴BE＝BG＝BT，

∵BC＝BD，∴EC＝DG，

∵∠D＝∠BAD＝∠FCE＝22.5°，∠CFE＝∠DFG，

∴△CFE≌△DFG(AAS)，∴CF＝DF，

∴AE－FG＝CT－FG＝CF＋GT＝EG＋DF.

(2)如图②，若∠CBD＝60°，当AC－DE＝6时，求DG2的值．

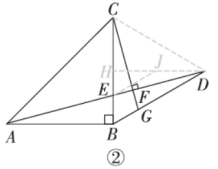
解：如图②中，连接CD，过点D作DH⊥BC于点H，在DH上取一点J，连接EJ，使得EJ＝DJ，设CF＝a.

∵CB＝BD，∠CBD＝60°，

∴△BCD是等边三角形，

∵AB＝BC，∠ABC＝90°，

∴∠ABD＝90°＋60°＝150°，

∠BAC＝∠ACB＝45°，

∴∠BAD＝∠BDA＝15°，∴∠CAF＝30°.

∵CG⊥AD，∴∠CFA＝90°，∴AC＝2CF＝2a，

∵∠CDB＝60°，∠CFD＝90°，

∴∠FDC＝∠FCD＝45°，

∴FC＝DF＝a，DC＝BC＝BD＝a.

∵DH⊥BC，

∴CH＝BH＝a，DH＝CH＝a，

设EH＝x，∵JE＝JD，∴∠JED＝∠JDE＝15°，

∴∠EJH＝∠JED＋∠JDE＝30°，

∴EJ＝2EH＝DJ＝2x，HJ＝x，

DE＝＝(＋)x，

∴x＋2x＝a，∴x＝a，

∴DE＝(3－)a.

∵AC－DE＝6，

∴2a－(3－)a＝6，∴a＝3(＋1)，

∴EC＝CH＋EH＝(－)a＝6.

∵∠CFE＝∠DFG＝90°，CF＝DF，

∠FCE＝∠FDG＝15°，

∴△CFE≌△DFG(ASA)，∴DG＝EC＝6，

∴DG2＝72.