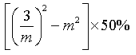2023年华师大版数学七年级上册《3.1 列代数式》课时练习(含答案)
展开2023年华师大版数学七年级上册
《3.1 列代数式》课时练习
A.a+b2 B.a2+b C.(a+b)2 D.a2+b2
2.苹果原价是每斤a元,现在按8折出售,假如现在要买一斤,那么需要付费( )
A.0.8a元 B.0.2a元 C.1.8a元 D.(a+0.8)元
3.一个两位数,个位数字为a,十位数字比个位数字大1,则这个两位数可表示为( )
A.11a-1 B.11a-10 C.11a+1 D.11a+10
4.某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )
A.(a-10%)(a+15%)万元 B.a(1-90%)(1+85%)万元
C.a(1-10%)(1+15%)万元 D.a(1-10%+15%)万元
5.某报亭老板以每份0.5元的价格从报社购进某种报纸500份,以每份0.8元的价格销售x份(x<500),未销售完的报纸又以每份0.1元的价格由报社收回,这次买卖中该老板赚钱( )
A.(0.7x﹣200)元 B.(0.8x﹣200)元 C.(0.7x﹣180)元 D.(0.8x﹣250)元
6.我们知道,用字母表示的代数式是具有一般意义的,请仔细分析下列赋予3a实际意义的例子中不正确的是( )
A.若葡萄的价格是3元/千克,则3a表示买a千克葡萄的金额
B.若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长
C.将一个小木块放在水平桌面上,若3表示小木块与桌面的接触面积,a表示桌面受到的压强,则3a表示小木块对桌面的压力
D.若3和a分别表示一个两位数中的十位数字和个位数字,则3a表示这个两位数
7.如图,一个窗户的上部是由4个扇形组成的半圆,下部是由4个边长相同的小正方形组成的长方形,则这个窗户的外框总长为( )
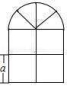
A.6a+πa B.12a C.15a+πa D.6a
8.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,…,依此类推,则由正n边形“扩展”而来的多边形的边数为( )

A.n(n﹣1) B.n(n+1) C.(n+1)(n﹣1) D.n2+2
10.某厂今年的产值a万元,若年平均增长率为x,则两年后的产值是 万元。
11.一个三位数,个位数字为a,十位数字比个位数字少2,百位数字比个位数字多1,那么这个三位数为________________.
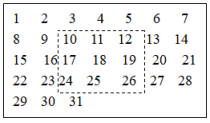
12.如图是某月份的月历,用正方形圈出9个数,设最中间一个是x,
则用x表示这9个数的和是___;
13.某班学生在实践基地进行拓展活动,因为器材的原因,教练要求分成固定的a组,若每组5人,则多出9名同学;若每组6人,最后一组的人数将不满,则最后一组的人数用含a的式子可表示为________.
14.下面是按照一定规律画![]() 出的一列“树型”图:[来源:学科网]
出的一列“树型”图:[来源:学科网]
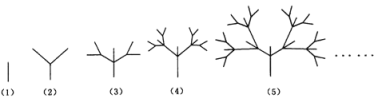
经观察可以发现:
图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出 个“树枝”.
(1)m的倒数的3倍与m的平方差的50%;
(2)x的与y的差的;
(3)甲数a与乙数b的差除以甲、乙两数的积.
16.学校多功能报告厅共有20排座位,其中第一排有a个座位,后面每排比前一排多2个座位.
(1)用式子表示最后一排的座位数.
(2)若最后一排有6![]() 0个座位,则第一排有多少个座位?
0个座位,则第一排有多少个座位?
17.如图是某居民小区的一块长为2a米,宽为b米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?

18.某商店有一种商品每件成本a元,原来按成本增加b元定价出售,售出40件后,由于库存积压减价,按售价的80%出售,又销售60件.
(1)销售100件这种商品的总售价为多少元?
(2)销售100件这种商品共盈利了多少元?
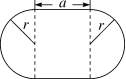
19.一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长l;
(2)花坛的面积S;
(3)若a=8m,r=5m,求此时花坛的周长及面积(π取3.14).
20.下面的图形是由边长为l的正方形按照某种规律排列而组成的.
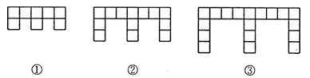
(1)观察图形,填写下表:
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
(2)(x﹣y);
(3)(a﹣b)÷ab.
16.解:(1)最后一排的座位数(单位:个)为a+2×19=a+38.
(2)由题意,得a+38=60,解得a=22.
若最后一排有60个座位,则第一排有22个座位.
17.解:花台面积为πa2平方米,草地面积为(2ab﹣πa2)平方米.
所需资金为100×πa2+50(2ab﹣πa2)=50πa2+100ab.
18.解:(1)根据题意,得40(a+b)+60(a+b)×80%=88a+88b(元),
则销售100件这种商品的总售价为(88a+88b)元.
(2)根据题意,得88a+88b-100a=-12a+88b(元),
则销售100件这种商品共盈利了(-12a+88b)元.
19.解:(1)l=2πr+2a.
(2)S=πr2+2ar.
(3)当a=8m,r=5m时,l=2π×5+2×8=10π+16≈47.4(m),
S=π×52+2×8×5=25π+80≈158.5(m2).
20.解:(1)∵n=1时,正方形有8个,即8=5×1+3,周长是18,即18=10×1+8;
n=2时,正方形有13个,即13=5×2+3,周长是28,即28=10×2+8;
n=3时,正方形有18个,即18=5×3+3,周长是38,即38=10×3+8;
(2)由(1)可知,n=n时,正方形有5n+3个,周长是10n+8.
(3)∵y=10n+8,x=5n+3,
∴y=2x+2.