2022-2023学年河北省唐山市冀东名校高二（下）期末数学试卷（含解析）

这是一份2022-2023学年河北省唐山市冀东名校高二（下）期末数学试卷（含解析），共21页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年河北省唐山市冀东名校高二（下）期末数学试卷
一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设集合A＝{x|x＜3x﹣1}，B＝{x|﹣1＜x＜3}，则A∪B＝（　　）
A．（﹣1，+∞） B． C．（﹣∞，3） D．
2．若复数z满足（1+i）z＝4﹣2i（i为虚数单位），则z的共轭复数＝（　　）
A．3+i B．3﹣i C．1+3i D．1﹣3i
3．已知幂函数，下列能成为“f（x）是R上奇函数”充分条件的是（　　）
A．m＝﹣3，n＝1 B．m＝1，n＝2 C．m＝2，n＝3 D．m＝1，n＝3
4．已知函数f（x）导函数f'（x）的图象如图所示，则（　　）

A．f（x）在（﹣∞，﹣2）上单调递增
B．f（x）在（0，3）上单调递减
C．f（x）在x＝0处取得最大值
D．f（x）在x＝﹣2处取得最小值
5．已知函数f（x）＝ex+e﹣x+lg|x|，则不等式f（x+1）＞f（2x﹣1）的解集为（　　）
A．（0，2） B．
C．（0，3） D．
6．已知函数f（x）＝x+，g（x）＝2x+a，若∀x1∈[，1]，∃x2∈[2，3]，使得f（x1）≥g（x2），则实数a的取值范围是（　　）
A．a≤1 B．a≥1 C．a≤2 D．a≥2
7．三个数的大小顺序为（　　）
A．b＜c＜a B．b＜a＜c C．c＜a＜b D．a＜b＜c
8．已知a＞0，b＞0，a+2b＝4，则ab的最大值是（　　）
A． B．2 C．4 D．3
二、多项选择题：本题共4小题，每小题5分，共20分。在每小题给出的四个选项中，有两个或两个以上选项符合题目要求，全部选对得5分，选对但不全的得2分，有选错的得0分。
（多选）9．若函数f（x）的单调递增区间为（1，+∞），则f（x）可能是（　　）
A．f（x）＝ln（x﹣2）+x B．
C． D．f（x）＝x（lnx﹣1）
（多选）10．已知函数f（x）＝|ex﹣1|，x1＜0，x2＞0，函数y＝f（x）的图象在点A（x1，f（x1））处的切线与在点B（x2，f（x2））处的切线互相垂直，且分别与y轴交于M、N两点，则（　　）
A．x1+x2为定值
B．x1x2为定值
C．直线AB的斜率取值范围是（0，+∞）
D．的取值范围是（0，1）
（多选）11．已知，则（　　）
A．f（x）为奇函数
B．f（x）在（﹣∞，0）⋃（0，+∞）上单调递减
C．f（x）值域为（﹣∞，﹣1）∪（1，+∞）
D．f（f（x））的定义域为{x|x≠0}
（多选）12．设e为自然对数的底数，函数，则下列结论正确的是（　　）
A．当a＝e时，f（x）无极值点
B．当a＞e时，f（x）有两个零点
C．当1＜a＜e时，f（x）有1个零点
D．当a≤1时，f（x）无零点
三、填空题：本题共4小题，每小题5分，共20分．
13．已知a＞0，b＞0，且2a⋅4b＝（2a）b，则a+b的最小值为 　 　．
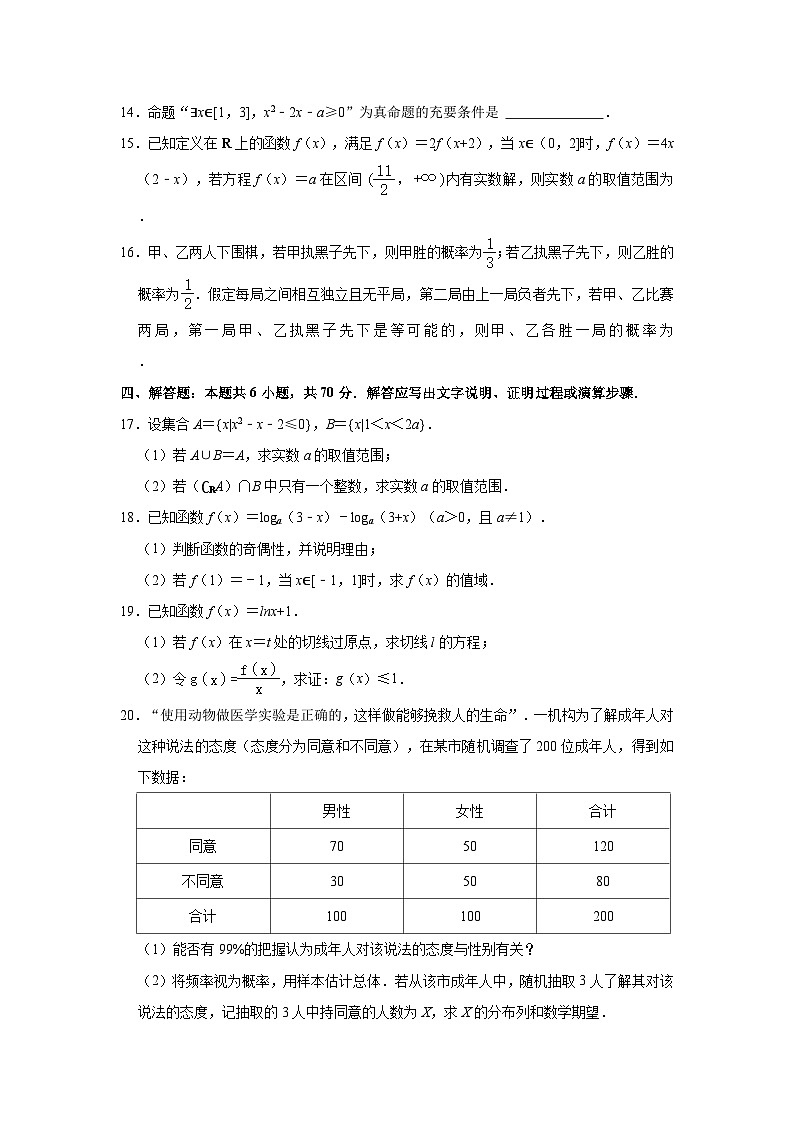
14．命题“∃x∈[1，3]，x2﹣2x﹣a≥0”为真命题的充要条件是 　 　．
15．已知定义在R上的函数f（x），满足f（x）＝2f（x+2），当x∈（0，2]时，f（x）＝4x（2﹣x），若方程f（x）＝a在区间内有实数解，则实数a的取值范围为 　 　．
16．甲、乙两人下围棋，若甲执黑子先下，则甲胜的概率为；若乙执黑子先下，则乙胜的概率为．假定每局之间相互独立且无平局，第二局由上一局负者先下，若甲、乙比赛两局，第一局甲、乙执黑子先下是等可能的，则甲、乙各胜一局的概率为 　 　．
四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．
17．设集合A＝{x|x2﹣x﹣2≤0}，B＝{x|1＜x＜2a}．
（1）若A∪B＝A，求实数a的取值范围；
（2）若（∁RA）∩B中只有一个整数，求实数a的取值范围．
18．已知函数f（x）＝loga（3﹣x）﹣loga（3+x）（a＞0，且a≠1）．
（1）判断函数的奇偶性，并说明理由；
（2）若f（1）＝﹣1，当x∈[﹣1，1]时，求f（x）的值域．
19．已知函数f（x）＝lnx+1．
（1）若f（x）在x＝t处的切线过原点，求切线l的方程；
（2）令，求证：g（x）≤1．
20．“使用动物做医学实验是正确的，这样做能够挽救人的生命”．一机构为了解成年人对这种说法的态度（态度分为同意和不同意），在某市随机调查了200位成年人，得到如下数据：

男性
女性
合计
同意
70
50
120
不同意
30
50
80
合计
100
100
200
（1）能否有99%的把握认为成年人对该说法的态度与性别有关？
（2）将频率视为概率，用样本估计总体．若从该市成年人中，随机抽取3人了解其对该说法的态度，记抽取的3人中持同意的人数为X，求X的分布列和数学期望．
附：，
P（χ2≥x0）
0.025
0.010
0.005
x0
5.024
6.635
7.879
21．下表是某农村居民2018年至2022年家庭人均收入（单位：万元）．
年份
2018
2019
2020
2021
2022
年份代码x
1
2
3
4
5
家庭人均收入y（万元）
1.2
1.4
1.5
1.6
1.8
（1）利用相关系数r判断y与x的相关关系的强弱（当0.75＜|r|≤1时，y与x的相关关系较强，否则相关关系较弱，精确到0.01）； （2）求y关于x的线性回归方程，并预测2023年该农村居民的家庭人均收入．附：对于一组数据（x1，y1）、（x2，y2）、…、（xn，yn），其回归直线的斜率和截距的最小二乘估计分别为，，样本相关系数r＝．参考数据：≈1.414．
22．已知函数f（x）＝ex﹣ax﹣1．
（1）讨论函数f（x）的单调性；
（2）若f（x）有且仅有2个零点，求实数a的取值范围．


参考答案
一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设集合A＝{x|x＜3x﹣1}，B＝{x|﹣1＜x＜3}，则A∪B＝（　　）
A．（﹣1，+∞） B． C．（﹣∞，3） D．
【分析】解不等式求集合A，再根据并集计算即可．
解：解不等式，即，
而B＝（﹣1，3），
所以A⋃B＝（﹣1，+∞）．
故选：A．
【点评】本题主要考查了集合并集运算，属于基础题．
2．若复数z满足（1+i）z＝4﹣2i（i为虚数单位），则z的共轭复数＝（　　）
A．3+i B．3﹣i C．1+3i D．1﹣3i
【分析】利用复数除法运算求出z，再利用共轭复数的定义求解作答．
解：依题意，，
所以z的共轭复数．
故选：C．
【点评】本题主要考查复数的四则运算，以及共轭复数的定义，属于基础题．
3．已知幂函数，下列能成为“f（x）是R上奇函数”充分条件的是（　　）
A．m＝﹣3，n＝1 B．m＝1，n＝2 C．m＝2，n＝3 D．m＝1，n＝3
【分析】根据函数奇偶性的性质判断即可．
解：对于A，f（x）＝x﹣3，定义域为{x|x≠0}，所以f（x）不是R上的奇函数，故A错误；
对于B，f（x）＝，定义域为[0，+∞），所以f（x）不是R上的奇函数，故B错误；
对于C，f（x）＝，定义域为R，且f（﹣x）＝＝＝＝f（x），故f（x）为偶函数，故C错误；
对于D，f（x）＝，定义域为R，且f（﹣x）＝＝﹣＝﹣f（x），故f（x）为奇函数，故D正确．
故选：D．
【点评】本题主要考查了函数奇偶性的判断，属于基础题．
4．已知函数f（x）导函数f'（x）的图象如图所示，则（　　）

A．f（x）在（﹣∞，﹣2）上单调递增
B．f（x）在（0，3）上单调递减
C．f（x）在x＝0处取得最大值
D．f（x）在x＝﹣2处取得最小值
【分析】由题意，根据导函数的正负和函数的单调性对选项进行逐一判断，进而即可求解．
解：由图象得当x＜﹣2时，f′（x）＜0，f（x）单调递减；
当﹣2＜x＜0，f′（x）＞0，f（x）单调递增；
当0＜x＜3时，f′（x）＜0，f（x）单调递减；
当x＞3，f′（x）＞0，f（x）单调递增，
当x＝﹣2时，函数f（x）取得极小值，并非最小值；
当x＝0时，函数f（x）取得极大值，并非最大值．
故选：B．
【点评】本题考查利用导数研究函数的单调性和极值，考查了逻辑推理和数形结合．
5．已知函数f（x）＝ex+e﹣x+lg|x|，则不等式f（x+1）＞f（2x﹣1）的解集为（　　）
A．（0，2） B．
C．（0，3） D．
【分析】依题意，可得偶函数f（x）＝ex+e﹣x+lg|x|在（0，+∞）上为增函数，不等式f（x+1）＞f（2x﹣1）⇔|x+1|＞|2x﹣1|，且x+1≠0，2x﹣1≠0，解之即可．
解：因为f（x）＝ex+e﹣x+lg|x|，x≠0，
所以f（﹣x）＝ex+e﹣x+lg|﹣x|＝ex+e﹣x+lg|x|＝f（x），
即f（x）为偶函数，
当x＞0时，f（x）＝ex+e﹣x+lgx，f′（x）＝ex﹣e﹣x+，
∵y＝ex与y＝﹣e﹣x在（0，+∞）上均为单调递增，
∴y＝ex﹣e﹣x在（0，+∞）上单调递增，
∴ex﹣e﹣x＞e0﹣＝0，
即当x＞0时，f′（x）＝ex﹣e﹣x+＞0恒成立，
∴偶函数f（x）＝ex+e﹣x+lg|x|在（0，+∞）上为增函数，
∴不等式f（x+1）＞f（2x﹣1）⇔|x+1|＞|2x﹣1|，且x+1≠0，2x﹣1≠0，
解得：0＜x＜，或＜x＜2．
即不等式f（x+1）＞f（2x﹣1）的解集为．
故选：B．
【点评】本题考查函数的奇偶性与单调性的综合应用，考查等价转化思想及运算求解能力，属于中档题．
6．已知函数f（x）＝x+，g（x）＝2x+a，若∀x1∈[，1]，∃x2∈[2，3]，使得f（x1）≥g（x2），则实数a的取值范围是（　　）
A．a≤1 B．a≥1 C．a≤2 D．a≥2
【分析】由∀x1∈[﹣1，2]，都∃x2∈[1，2]，使得f（x1）≥g（x2），可得f（x）＝x2+1在x1∈[﹣1，2]的最小值不小于g（x）＝ax+2在x2∈[1，2]的最小值，构造关于a的不等式组，可得结论．
解：当x1∈[，1]时，由f（x）＝x+得，f′（x）＝，
令f′（x）＞0，解得：x＞2，令f′（x）＜0，解得：x＜2，
∴f（x）在[，1]单调递减，
∴f（1）＝5是函数的最小值，
当x2∈[2，3]时，g（x）＝2x+a为增函数，
∴g（2）＝a+4是函数的最小值，
又∵∀x1∈[，1]，都∃x2∈[2，3]，使得f（x1）≥g（x2），
可得f（x）在x1∈[，1]的最小值不小于g（x）在x2∈[2，3]的最小值，
即5≥a+4，解得：a≤1，
故选：A．
【点评】本题考查的知识是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
7．三个数的大小顺序为（　　）
A．b＜c＜a B．b＜a＜c C．c＜a＜b D．a＜b＜c
【分析】据题意可设，求导，从而可根据导数符号得出f（x）在（e，+∞）上单调递减，并且可得出a＝f（e2），b＝f（4），c＝f（3），从而得出a，b，c的大小顺序．
解：设，，
∴x＞e时，f′（x）＜0，
∴f（x）在（e，+∞）上单调递减，
又，，且e2＞4＞3
∴f（e2）＜f（4）＜f（3），
∴a＜b＜c．
故选：D．
【点评】考查构造函数解决问题的方法，根据导数符号判断函数的单调性的方法，商的导数的计算公式，以及减函数的定义，对数的运算．
8．已知a＞0，b＞0，a+2b＝4，则ab的最大值是（　　）
A． B．2 C．4 D．3
【分析】根据基本不等式即可求解．
解：，
等号成立条件是a＝2b，即a+2b＝4b＝4时取等号，
即当且仅当a＝2，b＝1时取等号，
所以ab的最大值是2．
故选：B．
【点评】本题主要考查了基本不等式在最值求解中的应用，属于基础题．
二、多项选择题：本题共4小题，每小题5分，共20分。在每小题给出的四个选项中，有两个或两个以上选项符合题目要求，全部选对得5分，选对但不全的得2分，有选错的得0分。
（多选）9．若函数f（x）的单调递增区间为（1，+∞），则f（x）可能是（　　）
A．f（x）＝ln（x﹣2）+x B．
C． D．f（x）＝x（lnx﹣1）
【分析】利用导数与单调性的关系，逐一分析选项，即可得出答案．
解：对于A：f（x）＝ln（x﹣2）+x，则f'（x）＝＝，x∈（2，+∞），
∴f（x）的单调递增区间为（2，+∞），故A错误；
对于B：f（x）＝，则函数定义域为{x|x≠0}，f'（x）＝，
由f'（x）＝0得x＝1，由f'（x）＞0得x＞1，由f'（x）＜0得x＜0或0＜x＜1，
∴f（x）在（﹣∞，0）和（0，1）上单调递减，在（1，+∞）上单调递增，故B正确；
对于C：f（x）＝x+，则函数定义域为{x|x≠0}，f'（x）＝1﹣＝，
由f'（x）＝0得x＝±1，由f'（x）＞0得x＜﹣1或x＞1，由f'（x）＜0得﹣1＜x＜0或0＜x＜1，
∴f（x）在（﹣∞，﹣1）和（1，+∞）上单调递增，故C错误；
对于D：f（x）＝x（lnx﹣1），x∈（0，+∞），则f'（x）＝lnx﹣1+1＝lnx，
由f'（x）＝0得x＝1，由f'（x）＞0得x＞1，由f'（x）＜0得0＜x＜1，
∴f（x）在（0，1）上单调递减，在（1，+∞）上单调递增，故D正确．
故选：BD．
【点评】本题考查利用导数研究函数的单调性，考查转化思想，考查逻辑推理能力和运算能力，属于中档题．
（多选）10．已知函数f（x）＝|ex﹣1|，x1＜0，x2＞0，函数y＝f（x）的图象在点A（x1，f（x1））处的切线与在点B（x2，f（x2））处的切线互相垂直，且分别与y轴交于M、N两点，则（　　）
A．x1+x2为定值
B．x1x2为定值
C．直线AB的斜率取值范围是（0，+∞）
D．的取值范围是（0，1）
【分析】结合导数的几何意义可得x1+x2＝0，即可判断AB；结合基本不等式可判断C；结合直线方程及两点间距离公式可得|AM|，|BN|，化简可判断D．
解：当x＜0时，f（x）＝1﹣ex，导数为f′（x）＝﹣ex，
可得在点处的斜率为，
切线AM的方程为，
令x＝0，可得，即，
当x＞0时，f（x）＝ex﹣1，导数为f′（x）＝ex，
可得在点处的斜率为，
令x＝0，可得，即，
由f（x）的图象在A，B处的切线相互垂直，可得，
即为x1+x2＝0，x1＜0，x2＞0，故A正确，B错误；
直线AB的斜率，
因为x1≠x2，所以上面不等式中的等号不成立，故C正确；
，
，故D正确．
故答案为：ACD．
【点评】本题主要考查利用导数研究曲线上某点的切线方程，考查运算求解能力，属于中档题．
（多选）11．已知，则（　　）
A．f（x）为奇函数
B．f（x）在（﹣∞，0）⋃（0，+∞）上单调递减
C．f（x）值域为（﹣∞，﹣1）∪（1，+∞）
D．f（f（x））的定义域为{x|x≠0}
【分析】对于A，利用奇函数的定义即可判断；对于B，可以利用减函数的定义进行判断；对于C，可利用分离常数法进行求解；对于D，可利用定义域的性质进行求解．
解：对于A，由ex﹣1≠0，得x≠0，所以函数的定义域为{x|x≠0}，
又，所以f（x）为奇函数，故A正确；
对于B，设x1＜x2，x1，x2∈（﹣∞，0）⋃（0，+∞），
则，
因为x1＜x2，x1，x2∈（﹣∞，0）⋃（0，+∞），所以当x1＜0，x2＞0时，
，，所以，
则f（x1）＜f（x2），不符合单调递减函数的定义，故B错误；
对于C，因为，
又ex﹣1＞﹣1且ex﹣1≠0，所以，
则，故C正确；
对于D，由以上项分析函数f（x）的定义域为{x|x≠0}且f（x）≠0，故f（f（x））的定义域为{x|x≠0}，故D正确；
故选：ACD．
【点评】本题主要考查了函数的奇偶性，单调性的判断，还考查了函数定义域的求解及函数值域的求解，属于中档题．
（多选）12．设e为自然对数的底数，函数，则下列结论正确的是（　　）
A．当a＝e时，f（x）无极值点
B．当a＞e时，f（x）有两个零点
C．当1＜a＜e时，f（x）有1个零点
D．当a≤1时，f（x）无零点
【分析】求出函数的导数，取a＝e，得到A正确，通过讨论a的范围，求出函数的单调区间，结合函数的单调性判断BCD．
解：∵，∴f′（x）＝，
当a＝e时，（x﹣1）（ex﹣e）≥0，
故f′（x）≥0，f（x）无极值点，故A正确；
当a＞e时，lna＞1，x∈（0，1），（lna，+∞）时，f（x）递增，
x∈（1，lna）时，f（x）递减，且f（1）＝e﹣a＜0，
即在（lna，+∞）上f（x）有1个零点，故B错误；
当1＜a＜e时，0＜lna＜1，x∈（0，lna），（1，+∞）时，f（x）递增，
x∈（lna，1）时，f（x）递减，f（1）＝e﹣a＞0，
x∈（0，lna）上f（x）有1个零点，故C正确；
当a≤1时，ex﹣a≥0，f（x）在（0，1）递减，在（1，+∞）递增，
f（x）min＝f（1）＝e﹣a＞0，f（x）无零点，故D正确．
故选：ACD．
【点评】本题考查了函数的单调性，极值，零点问题，考查导数的应用以及分类讨论思想，是中档题．
三、填空题：本题共4小题，每小题5分，共20分．
13．已知a＞0，b＞0，且2a⋅4b＝（2a）b，则a+b的最小值为 　　．
【分析】先利用指数的运算与性质得到，再利用基本不等式“1”的妙用即可得解．
解：因为2a⋅4b＝（2a）b，所以2a⋅22b＝2ab，即2a+2b＝2ab，
则a+2b＝ab，所以，
又a＞0，b＞0，
所以，
当且仅当，即时，等号成立．
则a+b的最小值为．
故答案为：．
【点评】本题主要考查基本不等式及其应用，属于基础题．
14．命题“∃x∈[1，3]，x2﹣2x﹣a≥0”为真命题的充要条件是 　{a|a≤3}　．
【分析】原命题等价于∃x∈[1，3]使a≤x2﹣2x，求x2﹣2x在[1，3]上的最大值即可．
解：原命题可写为“∃x∈[1，3]，a≤x2﹣2x”，
当1≤x≤3时，x2﹣2x随x增大而增大，则x＝3时，x2﹣2x取最大值为3，所以a≤3．
故答案为：{a|a≤3}．
【点评】本题主要考查了含有量词的命题的真假关系的应用，属于基础题．
15．已知定义在R上的函数f（x），满足f（x）＝2f（x+2），当x∈（0，2]时，f（x）＝4x（2﹣x），若方程f（x）＝a在区间内有实数解，则实数a的取值范围为 　　．
【分析】将问题转化为y＝a与y＝f（x）的图象在内有交点，根据函数的递推关系，可得函数的部分解析式，作出y＝f（x）的图象，结合图象求解即可．
解：因为f（x）＝2f（x+2），
所以f（x﹣2）＝2f（x），f（x）＝f（x﹣2），
又因为当x∈（0，2]时，f（x）＝4x（2﹣x），
所以当x∈（2，4]时，x﹣2∈（0，2]，
所以f（x）＝f（x﹣2）＝×4（x﹣2）（4﹣x）＝2（x﹣2）（4﹣x），
当x∈（4，6]时，x﹣2∈（2，4]，
所以f（x）＝f（x﹣2）＝（x﹣4）（6﹣x），
所以f（）＝（﹣4）•（6﹣）＝，
……
作出函数f（x）的部分图象，如图所示：

又因为方程f（x）＝a在区间内有实数解，
即y＝a与y＝f（x）的图象在内有交点，
结合图象可知a∈[0，）．
故答案为：[0，）．
【点评】本题考查了转化思想、数形结合思想，关键点是作出函数y＝f（x）的图象，属于中档题．
16．甲、乙两人下围棋，若甲执黑子先下，则甲胜的概率为；若乙执黑子先下，则乙胜的概率为．假定每局之间相互独立且无平局，第二局由上一局负者先下，若甲、乙比赛两局，第一局甲、乙执黑子先下是等可能的，则甲、乙各胜一局的概率为 　　．
【分析】分两种情况讨论：（1）第一局甲胜，第二局乙胜：（2）第一局乙胜，第二局甲胜．分析出每局输赢的情况，结合独立事件和互斥事件的概率公式可求得所求事件的概率．
解：分两种情况讨论：
（1）第一局甲胜，第二局乙胜：
若第一局甲执黑子先下，则甲胜第一局的概率为，第二局乙执黑子先下，则乙胜的概率为，
若第一局乙执黑子先下，则甲胜第一局的概率为，第二局乙执黑子先下，则乙胜的概率为，
所以第一局甲胜，第二局乙胜的概率为；
（2）第一局乙胜，第二局甲胜：
若第一局甲执黑子先下，则乙胜第一局的概率为，第二局甲执黑子先下，则甲胜的概率为，
若第一局乙执黑子先下，则乙胜第一局的概率为，第二局甲执黑子先下，则甲胜的概率为，
所以，第一局乙胜，第二局甲胜的概率为．
综上所述，甲、乙各胜一局的概率为．
故答案为：．
【点评】本题主要考查了独立事件的概率乘法公式，属于基础题．
四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．
17．设集合A＝{x|x2﹣x﹣2≤0}，B＝{x|1＜x＜2a}．
（1）若A∪B＝A，求实数a的取值范围；
（2）若（∁RA）∩B中只有一个整数，求实数a的取值范围．
【分析】（1）解一元二次不等式得集合A，然后分和讨论可解；
（2）利用数轴分析即可求解．
解：（1）A＝{x|x2﹣x﹣2≤0}＝{x|﹣1≤x≤2}，
因为A∪B＝A，所以B⊆A，
当时，则B＝∅，故B⊆A符合题意，
当时，则B⊆A，可知2a≤2，即，
综上可知，a≤1，
故实数a的取值范围为（﹣∞，1]．
（2）∁RA＝{x|x＜﹣1或x＞2}，
因为（∁RA）∩B中只有一个整数，因此该整数为3，
如图，
由B＝{x|1＜x＜2a}，所以3＜2a≤4，解得，
故实数a的取值范围为．
【点评】本题主要考查集合的运算，属于基础题．
18．已知函数f（x）＝loga（3﹣x）﹣loga（3+x）（a＞0，且a≠1）．
（1）判断函数的奇偶性，并说明理由；
（2）若f（1）＝﹣1，当x∈[﹣1，1]时，求f（x）的值域．
【分析】（1）根据函数奇偶性的定义判断；
（2）由f（1）＝﹣1可求出a＝2，所以f（x）＝，再结合对数函数的性质求解即可．
解：（1）f（x）为奇函数，证明如下：
因为，
所以﹣3＜x＜3，
所以f（x）的定义域为（﹣3，3），
因为f（﹣x）＝loga（3+x）﹣loga（3﹣x）＝﹣f（x），
所以f（x）为奇函数；
（2）因为f（1）＝﹣1，
所以，
所以a＝2，
所以，
因为x∈[﹣1，1]，
所以3+x∈[2，4]，所以．
所以f（x）的值域为[﹣1，1]．
【点评】本题主要考查了函数的奇偶性的判断，考查了对数函数的性质，属于中档题．
19．已知函数f（x）＝lnx+1．
（1）若f（x）在x＝t处的切线过原点，求切线l的方程；
（2）令，求证：g（x）≤1．
【分析】（1）根据导数的几何意义，利用导数以及直线的点斜式方程求解．
（2）对函数进行求导，通过导数的正负确定函数的单调性，从而求出函数的最值，证明不等式即可．
解：（1）∵，
∴f（x）在x＝t处的切线的斜率为．
又（t，lnt+1）在曲线f（x）上，f（x）在x＝t处的切线过原点，
∴，
解得t＝1．
∴切线l的方程为y﹣1＝x﹣1，即y＝x．
（2）证明：∵，
∴，
由g′（x）＞0有：0＜x＜1，由g′（x）＜0有：x＞1，
∴g（x）在（0，1）上单调递增，在（1，+∞）上单调递减，
∴函数g（x）的最大值为g（1）＝f（1）＝1，
∴g（x）≤1．
【点评】本题考查导数的几何意义，考查利用导数研究函数的单调性及最值，考查不等式的证明，考查逻辑推理能力及运算求解能力，属于基础题．
20．“使用动物做医学实验是正确的，这样做能够挽救人的生命”．一机构为了解成年人对这种说法的态度（态度分为同意和不同意），在某市随机调查了200位成年人，得到如下数据：

男性
女性
合计
同意
70
50
120
不同意
30
50
80
合计
100
100
200
（1）能否有99%的把握认为成年人对该说法的态度与性别有关？
（2）将频率视为概率，用样本估计总体．若从该市成年人中，随机抽取3人了解其对该说法的态度，记抽取的3人中持同意的人数为X，求X的分布列和数学期望．
附：，
P（χ2≥x0）
0.025
0.010
0.005
x0
5.024
6.635
7.879
【分析】（1）由题意，根据所给信息，代入公式进行计算，根据与临界值比较即可得到答案；
（2）利用二项分布的概率公式求出分布列，再由期望的计算公式进行求解即可．
解：（1）假设成年人对该说法的态度与性别有关，
由列联表中数据可得χ2＝
＝≈8.333，
若成年人对该说法的态度与性别有关，
此时χ2≥6.635的概率约为0.01，
因为8.333＞6.635，
所以我们有99%的把握认为成年人对该说法的态度与性别有关；
（2）从该市成年人中所及抽取1人持同意态度的概率为＝，
所以X～B（3，），
此时P（x＝0）＝C（1﹣）3＝，
P（x＝1）＝C××（1﹣）2＝，
P（x＝2）＝C×（）2×（1﹣）＝，
P（x＝3）＝C×（）3＝，
X
0
1
2
3
P




则随机变量X的数学期望为
E（X）＝0×+1×+2×+3×＝．
【点评】本题考查独立性检验的实际应用，考查了逻辑推理和运算能力．
21．下表是某农村居民2018年至2022年家庭人均收入（单位：万元）．
年份
2018
2019
2020
2021
2022
年份代码x
1
2
3
4
5
家庭人均收入y（万元）
1.2
1.4
1.5
1.6
1.8
（1）利用相关系数r判断y与x的相关关系的强弱（当0.75＜|r|≤1时，y与x的相关关系较强，否则相关关系较弱，精确到0.01）； （2）求y关于x的线性回归方程，并预测2023年该农村居民的家庭人均收入．附：对于一组数据（x1，y1）、（x2，y2）、…、（xn，yn），其回归直线的斜率和截距的最小二乘估计分别为，，样本相关系数r＝．参考数据：≈1.414．
【分析】（1）由已知数据结合相关系数公式求得r值，与0.75比较大小得结论；
（2）利用最小二乘法求与的值，可得线性回归方程，取x＝6求得y值即可．
解：（1）由表中数据可得，，
，
，，，
∴r＝＝≈0.99＞0.75，
故y与x的相关关系较强；
（2）由（1）可知，，
∴，
，
则y关于x的线性回归方程为．
当x＝6时，．
故预测2022年该农村居民的家庭人均收入约为1.92万元．
【点评】本题考查利用最小二乘法求解相关系数和回归直线方程，考查运算求解能力，是基础题．
22．已知函数f（x）＝ex﹣ax﹣1．
（1）讨论函数f（x）的单调性；
（2）若f（x）有且仅有2个零点，求实数a的取值范围．
【分析】（1）根据题意，分a≤0和a＞0两种情况讨论求解即可；
（2）分别讨论a≤0，a＝1，a＞1，0＜a＜1，由f（x）的单调性及零点存在定理判断零点即可．
解：（1）f′（x）＝ex﹣a，
a≤0时，f′（x）＞0恒成立，f（x）在R上是增函数；
a＞0时，x＜lna时，f′（x）＜0，f（x）是减函数，x＞lna时，f′（x）＞0，f（x）是增函数；
综上，a≤0时，f（x）在R上是增函数，a＞0时，f（x）在（﹣∞，lna）上是减函数，在（lna，+∞）上是增函数；
（2）当a≤0时，由（1）得f（x）在R上是增函数，不符合题意；
当a＞0时，由（1）得f（x）≥f（lna）＝a﹣alna﹣1；
①当lna＝0⇒a＝1时，f（lna）＝f（0）＝0，f（x）只有一个零点，不符合题意；
②当lna＞0⇒a＞1时，f（lna）＜f（0）＝0，故f（x）在（﹣∞，lna）有一个零点，
又f（x）在（lna，+∞）上是增函数，
设g（a）＝f（a）＝ea﹣a2﹣1，h（a）＝g′（a）＝ea﹣2a，h′（a）＝ea﹣2＞h′（1）＞0，
∴g′（a）在（1，+∞）单调递增，g′（a）＞g′（1）＞0，
∴g（a）在（1，+∞）单调递增，f（a）＝g（a）＞g（1）＞0，
设m（x）＝x﹣lnx，由知，
当x∈（0，1），m′（x）＜0，m（x）单调递减，当x∈（1，+∞），m′（x）＞0，m（x）单调递增，
∴m（x）＝x﹣lnx≥m（1）＝1⇒x＞lnx，即a＞lna，
故f（x）在（lna，+∞）有一个零点，故函数有两个零点；
③当lna＜0⇒0＜a＜1时，f（lna）＜f（0）＝0，故（lna，+∞）有一个零点，
又f（x）在（﹣∞，lna）上是减函数，，由②得，
故f（x）在（﹣∞，lna）有一个零点，故函数有两个零点；
综上，0＜a＜1或a＞1，
实数a的取值范围为（0，1）∪（1，+∞）．
【点评】本题考查了导数的综合应用，属于中档题．