2022-2023学年江苏省南京市鼓楼区八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年江苏省南京市鼓楼区八年级（下）期末数学试卷（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年江苏省南京市鼓楼区八年级（下）期末数学试卷
学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）
一、选择题（本大题共6小题，共12.0分。在每小题列出的选项中，选出符合题目的一项）
1. 若式子 x−1在实数范围内有意义，则x的取值范围是(    )
A. x≠1 B. x>1 C. x≥1 D. x≤1
2. 为了解某校5000名学生的体重情况，随机抽取了200名学生的体重进行统计分析.在该问题中，下列说法正确的是(    )
A. 这200名学生是总体的一个样本 B. 每个学生是个体
C. 这5000名学生体重的全体是总体 D. 样本容量是200名学生
3. 袋子中装有2个黑球和1个白球，随机摸出两个球.下列事件是必然事件的是(    )
A. 摸出两个白球 B. 摸出一个白球一个黑球
C. 至少摸出一个黑球 D. 摸出两个黑球
4. 将分式2xy3x+2y中的x、y都扩大为原来的2倍，则分式的值(    )
A. 不变 B. 扩大为原来的2倍 C. 扩大为原来的4倍 D. 缩小到原来的12
5. 下列测量方案能判定四边形台面为矩形的是(    )
A. 测量得出对角线相等
B. 测量得出对角线互相平分
C. 测量得出两组对边分别相等
D. 测量得出对角线交点到四个顶点的距离相等
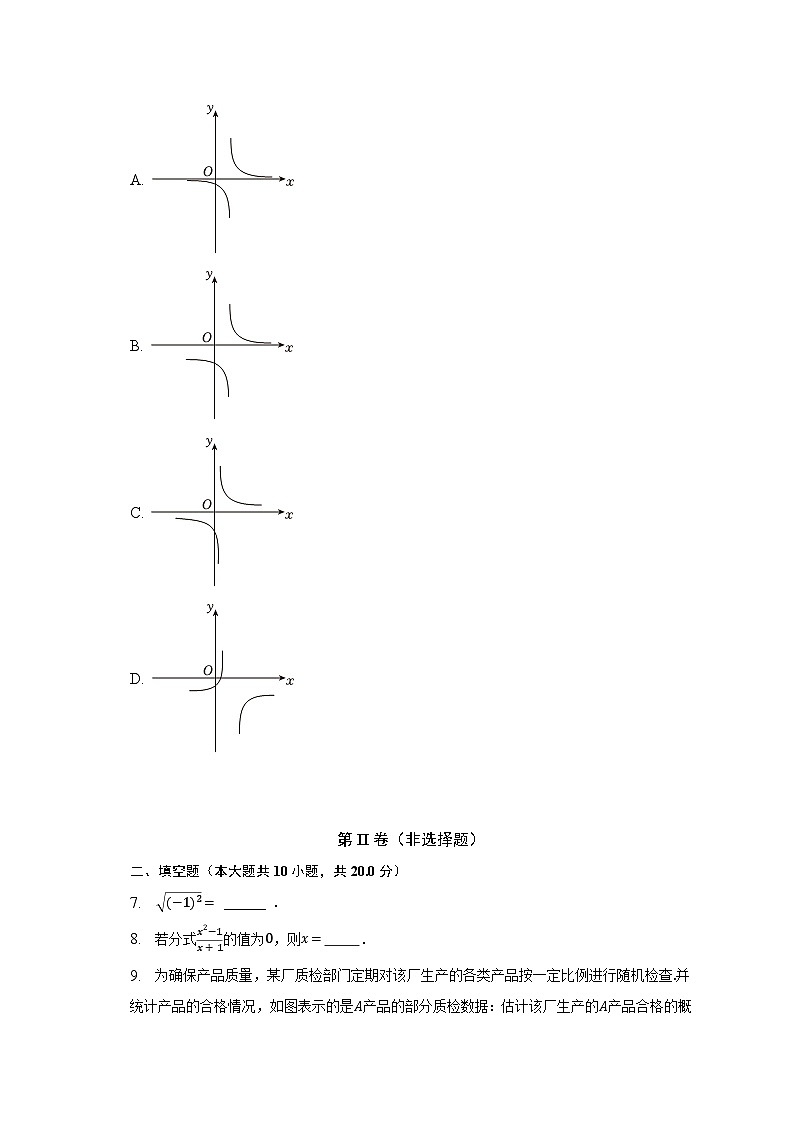
6. 函数y1=12x−1在平面直角坐标系中的图象如图所示，则在该平面直角坐标系中，函数y=1y1的大致图象是(    )
A.
B.
C.
D.


第II卷（非选择题）
二、填空题（本大题共10小题，共20.0分）
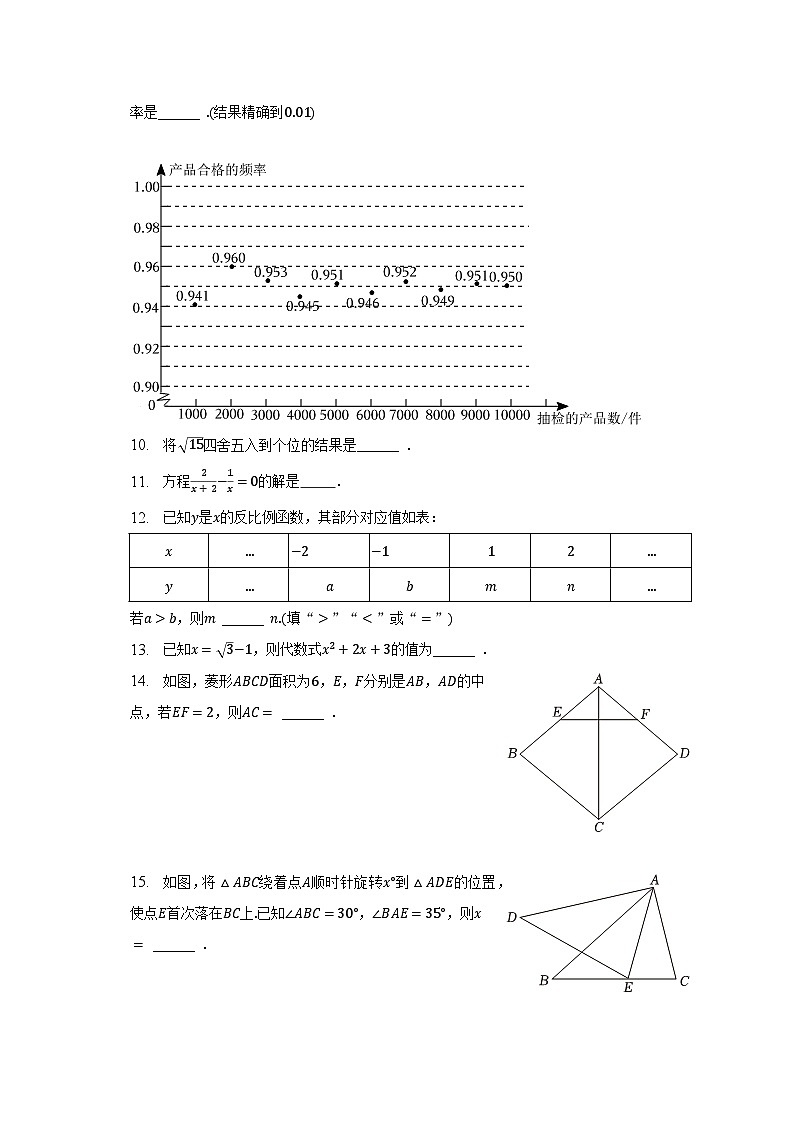
7. (−1)2= ______ ．
8. 若分式x2−1x+1的值为0，则x=          ．
9. 为确保产品质量，某厂质检部门定期对该厂生产的各类产品按一定比例进行随机检查.并统计产品的合格情况，如图表示的是A产品的部分质检数据：估计该厂生产的A产品合格的概率是______ .(结果精确到0.01)


10. 将 15四舍五入到个位的结果是______ ．
11. 方程2x+2−1x=0的解是          ．
12. 已知y是x的反比例函数，其部分对应值如表：
x
…
−2
−1
1
2
…
y
…
a
b
m
n
…
若a>b，则m ______ n.(填“>”“”“．
根据反比例函数的变化性质判断即可．
本题考查了反比例函数的性质，观察表格并得到条件是解题的关键．

13.【答案】5 
【解析】解：∵x= 3−1，
∴x+1= 3
∴x2+2x+3=(x+1)2+2=( 3)2+2=3+2=5．
故答案为：5．
先利用已知条件得x+1= 3，将所求代数式配方，然后利用整体代入的方法计算．
本题考查了二次根式的化简求值：二次根式的化简求值，一定要先化简再代入求值．

14.【答案】4 
【解析】解：连接BD，如图所示：

∵E、F分别是AB，AD的中点，且EF=2，
∴EF是△ABD的中位线，
∴BD=2EF=2×2=4，
∵AC、BD是正方形ABCD的对角线，
∴AC=BD=4．
故答案为：4
连接BD利用三角形中位线得出BD=2EF，再根据正方形性质求出AC即可．
本题主要考查正方形的性质和三角形中位线定理，关键是作辅助线构建三角形．

15.【答案】25 
【解析】解：过点A作AF⊥EC于F，

根据旋转的性质得：旋转角为∠CAE，AE=AC，
∴∠CAE=x°，
∵∠ABC=30°，∠BAE=35°，
∴∠AEC=∠ABC+∠BAE=65°，
∴∠EAF=90°−∠AEC=25°，
∵AE=AC，AF⊥EC，
∴∠EAF=∠CAF=25°，
∴∠CAE=∠EAF+∠CAF=50°．
∴x°=25°．
故答案为：25．
过点A作AF⊥EC于F，先根据旋转的性质得∠CAE=x°，由三角形的外角定理得∠AEC=65°，进而可求出∠EAF=25°，然后根据等腰三角形的性质得∠EAF=∠CAF=25°，据此可求出旋转角的度数．
此题主要考查了图形的旋转变换及性质，等腰三角形的性质，三角形的内角和定理等，解答此题的关键是准确识图，熟练掌握图形旋转变换的性质，理解等腰三角形底边上的高、底边上的中线、顶角的平分线重合(三线合一)．

16.【答案】(11,−5)或(11,5) 
【解析】解：∵A(8,a)，B(3,b)，
∴OA2=82+a2=a2+64，OB2=32+b2=b2+9，
AB2=(8−3)2+(a−b)2=(a−b)2+25，
∵四边形AOBC为正方形，
∴OA=OB，∠AOB=90°，
∴a2+64=b2+9，
整理得：b2−a2=55，
在Rt△AOB中，由勾股定理得：AB2=OA2+OB2，
∴(a−b)2+25=a2+64+b2+9，
整理得：ab=−24，
∴b=−24a，
将b=−24a代入b2−a2=55，得：(−24a)2−a2=55，
整理得：a4+55a2−576=0，
∴(a2+64)(a2−9)=0，
∵a2+64>0，
∴a2−9=0，
∴a=±3，
①当a=3时，b=−8，②当a=−3时，b=8，
设正方形AOBC的对角线AB，OC交于点Q，
点C(m,n)，
∵点Q既是AB的中点又是OC的中点，
12×(8+3)=12(m+0)，12(a+b)=12(n+0)，
∴m=11，n=a+b，
①当a=3时，b=−8时，n=a+b=−5，
此时点C的坐标为(11,−5)，
②当a=−3时，b=8时，n=a+b=5，
此时点C的坐标为(11,5)．
综上所述：点C的坐标为(11,−5)或(11,5)．
故答案为：(11,−5)或(11,5)．
根据点A，B坐标得OA2=a2+64，OB2=b2+9，AB2=(a−b)2+25，由正方形的性质得OA=OB得b2−a2=55，AB2=OA2+OB2，即(a−b)2+25=a2+64+b2+9，整理得ab=−24，据此解方程组得a=3，b=−8，过a=−3，b=8，设正方形AOBC的对角线AB，OC交于点Q，点C(m,n)，根据中点坐标公式得12×(8+3)=12(m+0)，12(a+b)=12(n+0)，进而可求出点C的坐标．
此题主要考查了正方形的性质，二元二次方程组的应用等，解答此题的关键是根据正方形的性质构造出关于a，b的方程，通过解方程组求出a，b的值进而确定点C的坐标．

17.【答案】解：(1) 24− 16− 6
=2 6− 66− 6
=5 66；
(2)( 48+14 6)÷ 27
= 48 27+ 64 27
=43+ 212
=16+ 212． 
【解析】(1)先把每一个二次根式化成最简二次根式，然后再进行计算即可解答；
(2)利用二次根式的除法法则，进行计算即可解答．
本题考查了二次根式的混合运算，准确熟练地进行计算是解题的关键．

18.【答案】解：(1)mm−1−3m−1m2−1
=mm−1−3m−1(m+1)(m−1)
=m(m+1)−(3m−1)(m+1)(m−1)
=m2−2m+1(m+1)(m−1)
=(m−1)2(m+1)(m−1)
=m−1m+1；
(2)(a+2+1a)÷(a−1a)
=a2+2a+1a÷a2−1a
=(a+1)2a⋅a(a+1)(a−1)
=a+1a−1． 
【解析】(1)利用异分母分式加减法法则，进行计算即可解答；
(2)先利用异分母分式加减法法则计算括号里，再算括号外，即可解答．
本题考查了分式的混合运算，熟练掌握因式分解是解题的关键．

19.【答案】解：设这种大米的原价是每千克x元，
根据题意，得105x+1400.8x=40，
解得：x=7．
经检验，x=7是原方程的解．
答：这种大米的原价是每千克7元． 
【解析】本题考查分式方程的应用，分析题意，找到合适的等量关系是解决问题的关键．
设这种大米的原价是每千克x元，根据两次一共购买了40kg列出方程，求解即可．

20.【答案】4  5− 2 
【解析】解：(1)设−2与x是关于1的一组“关联数”，
∴−2+x2=1，
解得：x=4，
∴−2与4是关于1的一组“关联数”，
故答案为：4；
(2)设 2+1与y是关于3的一组“关联数”，
∴ 2+1+y2=3，
解得：y=5− 2，
∴ 2+1与5− 2是关于3的一组“关联数”，
故答案为：5− 2；
(3)a2与b2是关于3的一组“关联数”，
理由：∵a= 2+1,b= 2−1，
∴a2+b22=( 2+1)2+( 2−1)22
=3+2 2+3−2 22
=62
=3，
∴a2与b2是关于3的一组“关联数”．
(1)设−2与x是关于1的一组“关联数”，根据“关联数”的定义，进行计算即可解答；
(2)设 2+1与y是关于3的一组“关联数”，根据“关联数”的定义，进行计算即可解答；
(3)先计算出a2+b22的值，然后根据关联数”的定义，即可解答．
本题考查了二次根式的混合运算，理解“关联数”是解题的关键．

21.【答案】B  D  6.2  8.50%，而男生优秀率11.%，女生优秀率6.2%，
∴男生人数小于女生人数，
故答案为：6.2%，