
高中数学北师大版 (2019)必修 第一册第一章 预备知识4 一元二次函数与一元二次不等式4.1 一元二次函数同步练习题
展开第二章 一元二次函数、方程和不等式
第一节 不等式的性质
1.(2023甲卷文科11)已知函数![]() .记
.记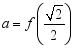 ,
,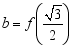 ,
, ,则 ( )
,则 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【分析】利用作差法比较自变量的大小,再根据指数函数的单调性及二次函数的性质判断即可.
【解析】令![]() ,则
,则![]() 开口向下,对称轴为
开口向下,对称轴为![]() ,
,
因为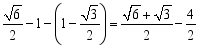 ,而
,而![]() ,
,
所以![]()
由二次函数性质知![]() ,
,
因为 ,
,
而![]() ,
,
即![]() ,所以
,所以![]() ,
,
综上,![]() ,
,
又![]() 为增函数,故
为增函数,故![]() ,即
,即![]() .
.
故选A.
2.(2023新高考I卷10)噪声污染问题越来越受到重视,用声压级来度量声音的强弱,定义声压级![]() ,其中常数
,其中常数![]() 是听觉下限阈值,
是听觉下限阈值,![]() 是实际声压.下表为不同声源的声压级:
是实际声压.下表为不同声源的声压级:
声源 | 与声源的距离/m | 声压级/dB |
燃油汽车 | 10 | 60~90 |
混合动力汽车 | 10 | 50~60 |
电动汽车 | 10 | 40 |
已知在距离燃油汽车、混合动力汽车、电动汽车10m处测得实际声压分别为![]() ,
,![]() ,
,![]() ,则( )
,则( )
-
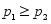 B.
B.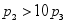 C.
C.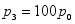 D.
D.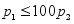
【解析】选项A,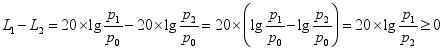 ,所以
,所以![]() ,所以A正确;
,所以A正确;
选项B,![]() ,所以
,所以![]() ,所以
,所以![]() ,故B错误;
,故B错误;
选项C,![]() ,所以
,所以![]() ,所以
,所以![]() ,故C正确;
,故C正确;
选项D,![]() ,所以
,所以![]() ,所以
,所以![]() ,故D正确.
,故D正确.
故选ACD.
第二节 三个“二次”的关系
1.(2023甲卷文科11)已知函数![]() .记
.记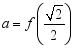 ,
,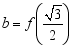 ,
, ,则 ( )
,则 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【分析】利用作差法比较自变量的大小,再根据指数函数的单调性及二次函数的性质判断即可.
【解析】令![]() ,则
,则![]() 开口向下,对称轴为
开口向下,对称轴为![]() ,
,
因为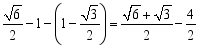 ,而
,而![]() ,
,
所以![]()
由二次函数性质知![]() ,
,
因为 ,
,
而![]() ,
,
即![]() ,所以
,所以![]() ,
,
综上,![]() ,
,
又![]() 为增函数,故
为增函数,故![]() ,即
,即![]() .
.
故选A.
2.(2023新高考I卷1)已知集合![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【解析】![]() ,所以
,所以![]() ,故选C.
,故选C.
11.(2023新高考I卷4)设函数![]() 在区间
在区间![]() 单调递减,则
单调递减,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【解析】令![]() ,要使得
,要使得![]() 在区间
在区间![]() 单调递减,需要满足
单调递减,需要满足![]() 在区间
在区间![]() 单调递减,所以
单调递减,所以![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
故选D.
第三节 基本不等式
无
北师大版 (2019)必修 第一册第一章 预备知识4 一元二次函数与一元二次不等式4.1 一元二次函数达标测试: 这是一份北师大版 (2019)必修 第一册第一章 预备知识4 一元二次函数与一元二次不等式4.1 一元二次函数达标测试,共4页。试卷主要包含了用不等号“>”或“<”填空,求下列不等式的解集等内容,欢迎下载使用。
高考真题解析2 一元二次函数、方程和不等式: 这是一份高考真题解析2 一元二次函数、方程和不等式,共4页。
高中人教A版 (2019)第二章 一元二次函数、方程和不等式本章综合与测试课后复习题: 这是一份高中人教A版 (2019)第二章 一元二次函数、方程和不等式本章综合与测试课后复习题,共13页。试卷主要包含了已知,,则,的大小关系是,不等式的解集为,下列不等式中,正确的是,已知,则的最大值为,设,为正数,且,则的最小值为,下列命题中,正确的是,若,,且,则的最小值为,下列不等式正确的是等内容,欢迎下载使用。













