













人教版八年级上册第十二章 全等三角形12.3 角的平分线的性质教学课件ppt
展开12.3.2 角的平分线的判定
人教版数学八年级上册
1.理解角平分线的判定定理.(难点)2.掌握角平分线判定定理内容的证明方法并应用其解题.(重点)3.学会判断一个点是否在一个角的平分线上.
文字语言:角平分线上的点到角的两边的距离相等.
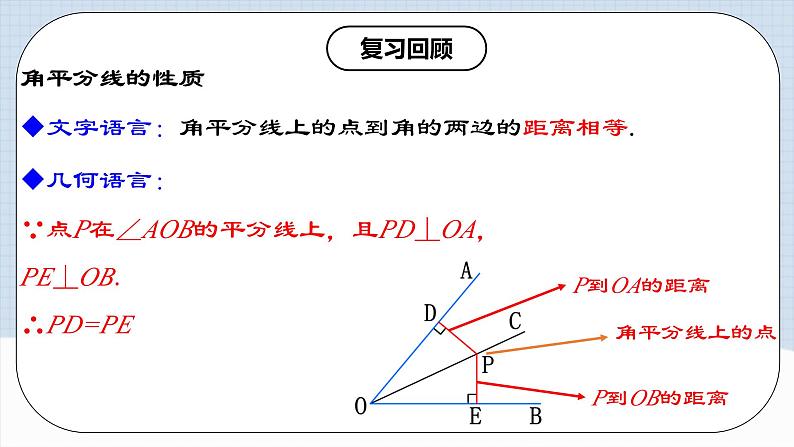
角平分线的性质
几何语言:
∵点P在∠AOB的平分线上,且PD⊥OA,PE⊥OB.∴PD=PE
P到OA的距离
P到OB的距离
角平分线上的点
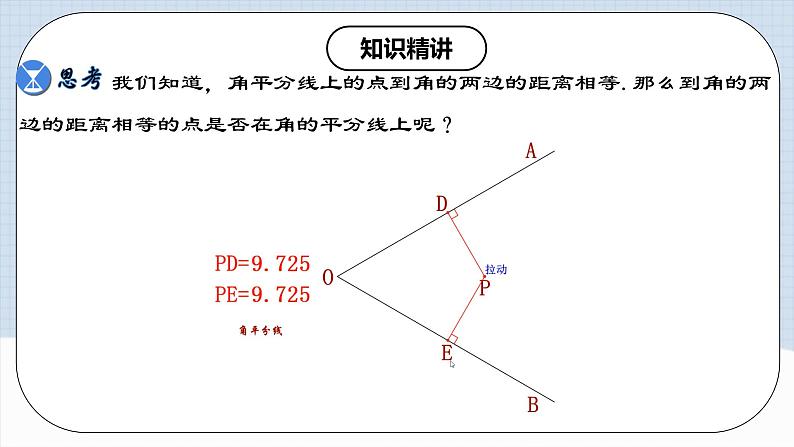
我们知道,角平分线上的点到角的两边的距离相等.那么到角的两边的距离相等的点是否在角的平分线上呢?
猜想:角的内部到角的两边的距离相等的点在角的平分线上.
一般情况下,我们要证明一个几何命题时,可以按照类似的步骤进行,即1.明确命题中的已知和求证;2.根据题意,画出图形,并用数学符号表示已知和求证;3.经过分析,找出由已知推出要证的结论的途径,写出证明过程.
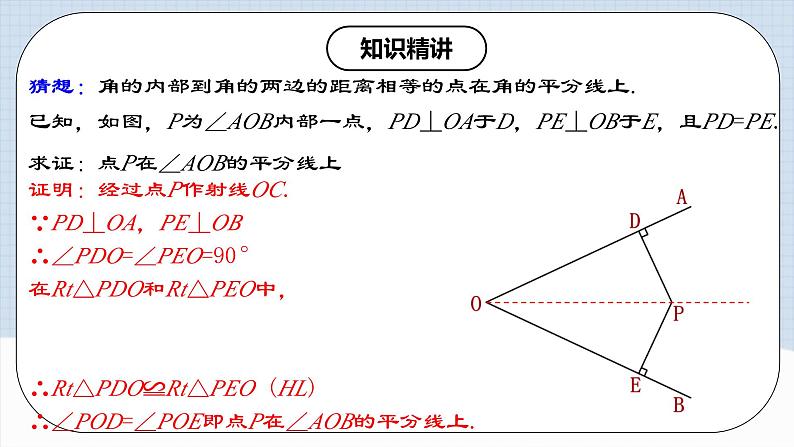
已知,如图,P为∠AOB内部一点,PD⊥OA于D,PE⊥OB于E,且PD=PE. 求证:点P在∠AOB的平分线上
猜想:角的内部到角的两边的距离相等的点在角的平分线上.
证明:经过点P作射线OC. ∵PD⊥OA,PE⊥OB ∴∠PDO=∠PEO=90° 在Rt△PDO和Rt△PEO中, ∴Rt△PDO≌Rt△PEO (HL) ∴∠POD=∠POE即点P在∠AOB的平分线上.
文字语言:角的内部到角的两边的距离相等的点在角的平分线上.
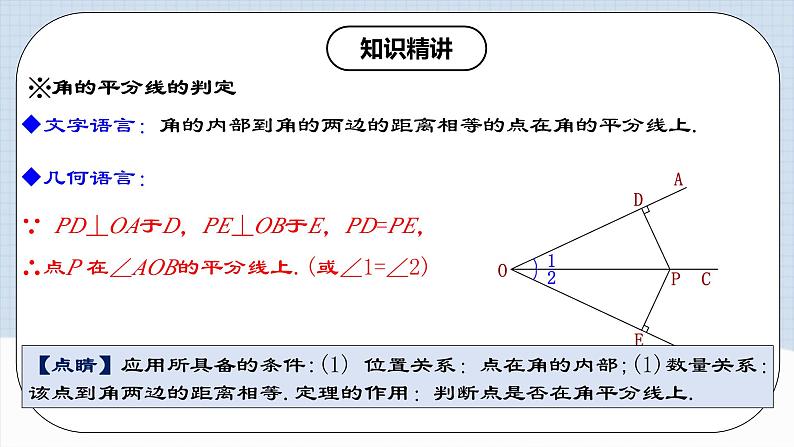
※角的平分线的判定
几何语言:
∵ PD⊥OA于D,PE⊥OB于E,PD=PE,∴点P 在∠AOB的平分线上.(或∠1=∠2)
【点睛】应用所具备的条件:(1) 位置关系:点在角的内部;(1)数量关系:该点到角两边的距离相等.定理的作用:判断点是否在角平分线上.
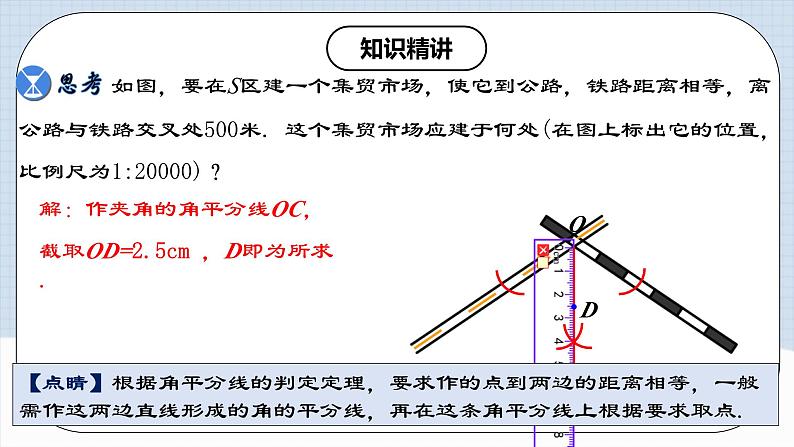
如图,要在S区建一个集贸市场,使它到公路,铁路距离相等,离公路与铁路交叉处500米. 这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)?
D
O
C
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
【点睛】根据角平分线的判定定理,要求作的点到两边的距离相等,一般需作这两边直线形成的角的平分线,再在这条角平分线上根据要求取点.
如图,在直线MN上求作一点P,使点P到射线OA和OB的距离相等.
则:点P为所求.
P
例1.已知:如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB,BC,CA的距离相等.
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,∴PD=PE.同理PE=PF.∴PD=PE=PF.即点P到三边AB,BC,CA的距离相等.
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
【归纳】三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
例2.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( ) A.110° B.120° C.130° D.140°
A
例3.如图,PA、PC分别是△ABC外角∠MAC与∠NCA的平分线,它们交于点P,PD⊥BM于D,PF⊥BN于F.求证:BP为∠MBN的平分线.
证明:过P作PE⊥AC于E.∵PA平分∠MAC,且PD⊥BM,PE⊥AC∴PD=PE∵PC平分∠NCA,且PF⊥BN,PE⊥AC∴PF=PE∴PD=PF∵PD⊥BM,PF⊥BN∴P在∠MBN的平分线上即BP为∠MBN的平分线.
如图,△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于点P. 求证:点P到三边AB,BC,CA所在直线的距离相等.
证明:过P点做PF⊥AC,PG⊥BC,PH⊥AB,垂足分别是F,G,H.∵BD、CE分别是∠ABC、∠ACB的外角的平分线 ∴PG=PH,PF=PG ∴PF=PG=PH即点P到三边AB,BC,CA所在直线的距离相等.
例4.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:(1)AM平分∠DAB;(2)AD=AB+CD.
证明:(1)作MN⊥AD于N.∵DM平分∠ADC,且MC⊥CD,MN⊥AD∴CM=MN∵M是BC的中点∴CM=MB∴MN=MB∵MB⊥BA,MN⊥AD,且MN=MB∴AM平分∠DAB
例4.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:(1)AM平分∠DAB;(2)AD=AB+CD.
1.如图,PD⊥OA于D,PE⊥OB于E,PD=6cm,当PE=____cm时,点P在∠AOB的平分线上.2.如图,已知PA⊥ON于A,PB⊥OM于B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA=______.
6
55°
3.如图,直线l1,l2,l3表示三条两两相互交叉的公路,现在拟建一个货物中转站,要求它到三条公路的距离都相等,则可供选择的地址有____处.4.如图所示,已知△ABC的周长是10,OC、OB分别平分∠ABC和∠ACB,OD上BC于D,且OD=1,则△ABC的面积是_______.
4
5
5.如图,某市有一块由三条马路围成的三角形绿地,现准备在绿地中建一小亭供人小憩,使小亭中心到三条马路的距离相等,试确定小亭的中心位置.
解:点P为所求.
6.如图,有一块三角形的闲地,其三边长分别为30m、40m、50m,现要把它分成面积比为3:4:5的三部分,分别种植不同的花,请你设计一种方案,并简要说明理由.
解:点P即为所求,即△ABC分为△ABP、△ACP、△BCP三个小三角形,即可符合面积比为3:4:5.
7.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC.求证:AD是∠BAC的平分线.
初中数学人教版八年级上册15.2.1 分式的乘除教学课件ppt: 这是一份初中数学人教版八年级上册15.2.1 分式的乘除教学课件ppt,文件包含1522分式的乘方pptx、1522分式的乘方同步练习解析版docx、1522分式的乘方教学设计docx、1522分式的乘方同步练习原卷版docx、1522分式的乘方导学案docx等5份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
初中人教版15.2.1 分式的乘除公开课教学作业ppt课件: 这是一份初中人教版15.2.1 分式的乘除公开课教学作业ppt课件,文件包含1521分式的乘除pptx、1521分式的乘除同步练习解析版docx、1521分式的乘除教学设计docx、1521分式的乘除同步练习原卷版docx、1521分式的乘除导学案docx等5份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
初中数学人教版八年级上册14.1.3 积的乘方精品教学作业课件ppt: 这是一份初中数学人教版八年级上册14.1.3 积的乘方精品教学作业课件ppt,文件包含1413积的乘方pptx、1413积的乘方同步练习解析版docx、1413积的乘方教学设计docx、1413积的乘方同步练习原卷版docx、1413积的乘方导学案docx等5份课件配套教学资源,其中PPT共20页, 欢迎下载使用。














