(新高一)初升高数学暑假衔接班精品讲义2.4.4 函数的单调性（2份打包，学生版+教师版）

这是一份(新高一)初升高数学暑假衔接班精品讲义2.4.4 函数的单调性（2份打包，学生版+教师版），文件包含新高一初升高数学暑假衔接班精品讲义244函数的单调性教师版doc、新高一初升高数学暑假衔接班精品讲义244函数的单调性学生版doc等2份试卷配套教学资源，其中试卷共18页， 欢迎下载使用。

第2.4章 函数的概念与性质
2.4.4 函数的单调性

高中要求
1通过已学过的函数特别是二次函数，理解这些函数的单调性、最大（小）值及其几何意义；
2 会用函数单调性的定义判断函数的单调性；

1 函数单调性的概念
(1)增函数和减函数
一般地，设函数的定义域为，区间:
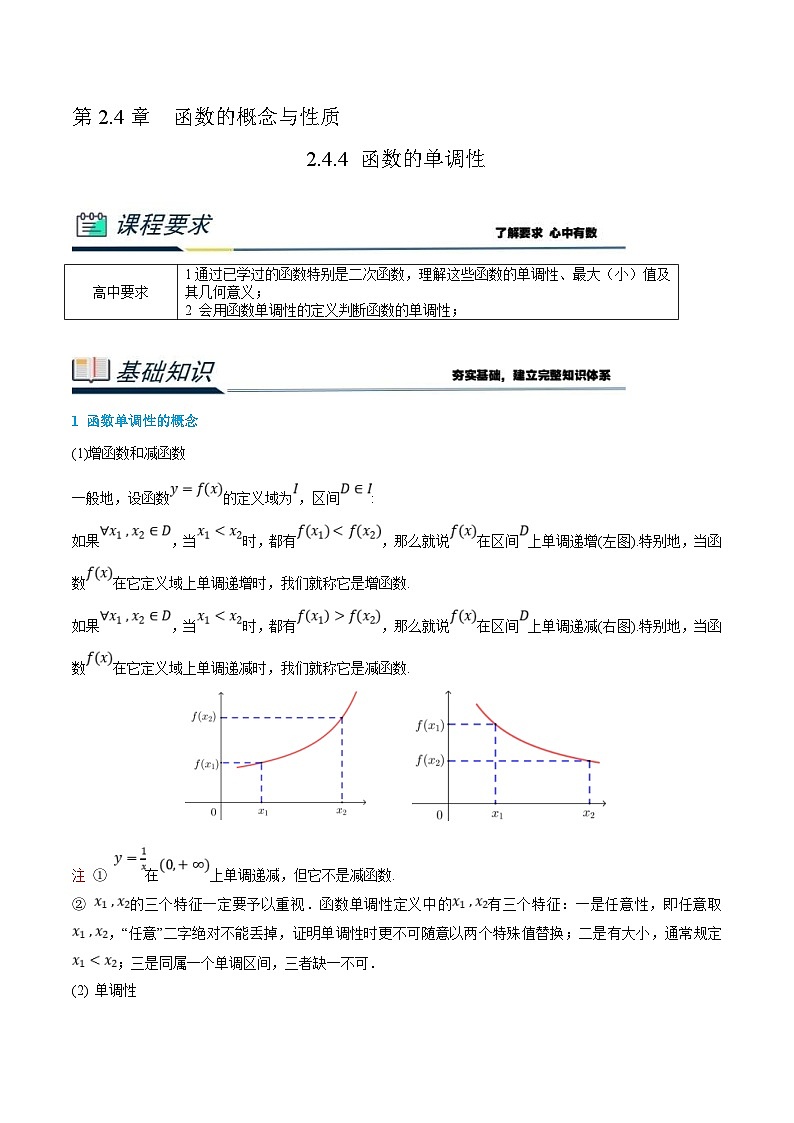
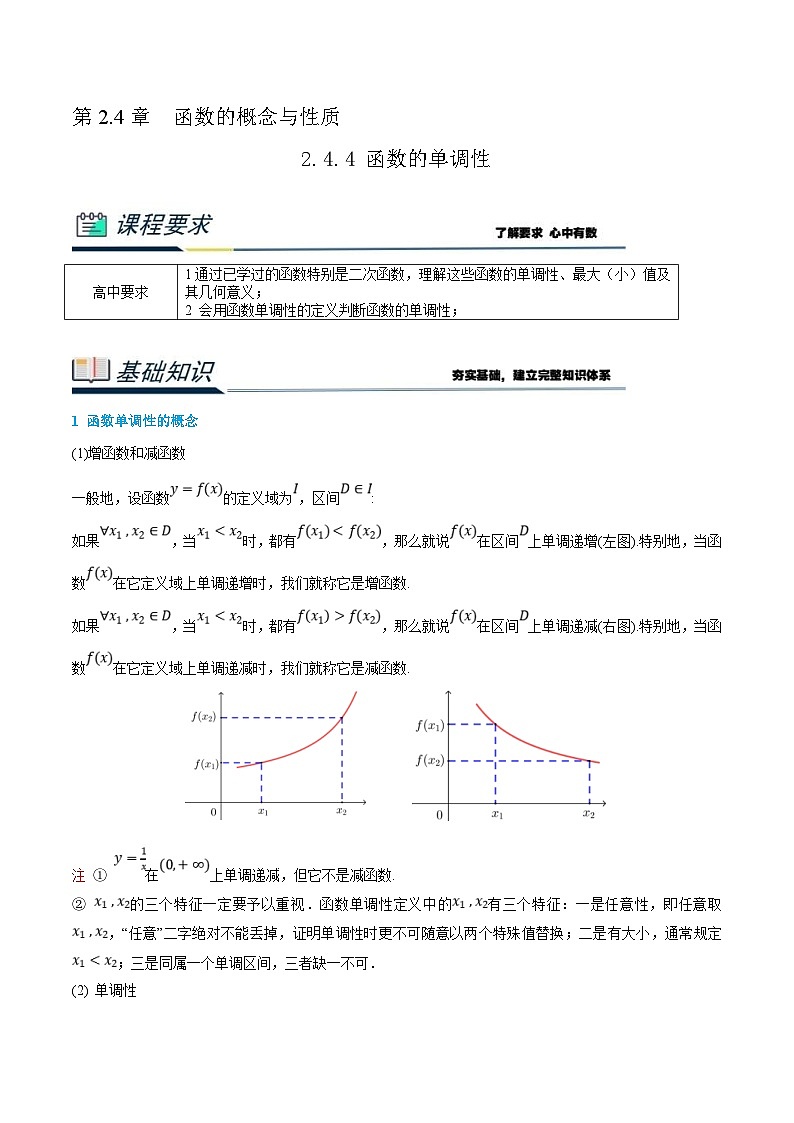
如果，当时，都有，那么就说在区间上单调递增(左图).特别地，当函数在它定义域上单调递增时，我们就称它是增函数.
如果，当时，都有，那么就说在区间上单调递减(右图).特别地，当函数在它定义域上单调递减时，我们就称它是减函数.

注 ① 在上单调递减，但它不是减函数.
② 的三个特征一定要予以重视．函数单调性定义中的有三个特征：一是任意性，即任意取，“任意”二字绝对不能丢掉，证明单调性时更不可随意以两个特殊值替换；二是有大小，通常规定；三是同属一个单调区间，三者缺一不可．
(2) 单调性
如果函数在区间上是增函数或减函数，那么就说函数在这一区间具有(严格的)单调性．区间叫做函数的单调区间．
注 ① 这个区间可以是整个定义域也可以是定义域的一部分.
② 有的函数无单调性．如函数，它的定义域是，但无单调性可言．
2 单调性概念的拓展
① 若递增，，则.
② 若递增，，则.
递减，有类似结论！
3 判断函数单调性的方法
① 定义法
解题步骤
(1) 任取，且；
(2) 作差；
(3) 变形(通常是因式分解和配方)；
(4) 定号(即判断差的正负)；
(5) 下结论(指出函数在给定的区间上的单调性)．
② 数形结合
③ 性质法
增函数+增函数增函数，减函数+减函数减函数；
但增函数增函数不一定是增函数，比如，均是增函数，而不是.










【题型1】 函数单调性的定义
【典题1】 判断在的单调性.












变式练习
1.函数在上是减函数，则有(　　)
A． B． C． D．
2.下列函数中，在区间上为增函数的是 ( )
B． C． D．
3.已知是定义在上单调递增的函数，则满足的取值范围是(　　)
A． B． C． D．
4.已知函数的单调增区间为　 　．
5.试用函数单调性的定义判断函数在区间上的单调性．




6.已知函数
(1)用函数单调性的定义证明在区间上为增函数
(2)解不等式：








【题型2】 参数问题
【典题1】若函数在区间上是增函数，在区间上是减函数，则实数的取值范围是(　　)








变式练习
1.已知函数是上的增函数，则(　　)
A． B． C． D．
2.函数在区间上是单调函数，则实数的取值范围是
3.若函数在区间上单调递减，则实数的取值范围是　 ．

1.函数在和都是增函数，若，且那么( )
A． B． C． D．无法确定
2.在区间上不是增函数的函数是 ( )
A． B． C． D．
3.函数的递减区间为(　　)

4.设是上的减函数，则(　　)


5.函数的单调递减区间为　 　．
6.若是上的单调减函数，则实数的取值范围为　 　．
7.已知函数，若则实数的取值范围是　 　．
8.已知函数，且
(1)求的值；
(2)判断在上的单调性，并给予证明；












9.已知函数是定义在上的增函数，且，，
解不等式．