人教A版 (2019)必修 第二册8.1 基本立体图形教学设计

教学设计标题：8.1.1基本立体图形（1）

学情分析：学生刚接触立体几何，缺乏空间想象能力，在教学中应注意促进学生主动探究的学习方式的形成，帮助学生完善思维结构发展空间想象能力，倡导学生积极主动，勇于探索的学习方法。同时，使学生进一步体会比较、化归、分析等一般科学方法的运用。

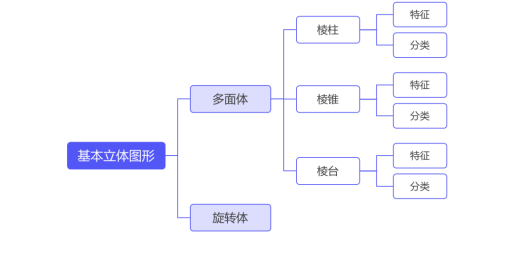
教学目标：

了解空间几何体的概念及分类

了解多面体及旋转体的概念

掌握棱柱、棱锥、棱台的概念

培养学生的数学抽象、直观想象等数学核心素养

教学重难点：

重点：通过对实物模型的观察，归纳认知棱柱、棱锥、棱台的结构特征

难点：理解棱柱、棱锥、棱台之间的关系

教学过程：

一.直接引入

在我们周围存在着各种各样的物体，它们都占据着空间的一部分。如果只考虑这些物体的形状和大小，而不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体．

设计意图：让学生快速进入学习状态

二．探究新知

观察图片,这些图片中的物体具有怎样的形状?在日常生活中,我们把这些物体的形状叫做什么?如何描述它们的形状?

设计意图：通过具体的实物图片，将学生们带入本节的教学氛围，引发学生的探究兴趣，并根据讨论结果，给出多面体及旋转体的概念。

多面体的定义:一般地,由若干个平面多边形的几何体叫做多面体,围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点. 

旋转体的定义:一条平面曲线（包括直线）绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体,这条定直线叫做旋转体的轴. 

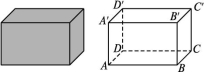
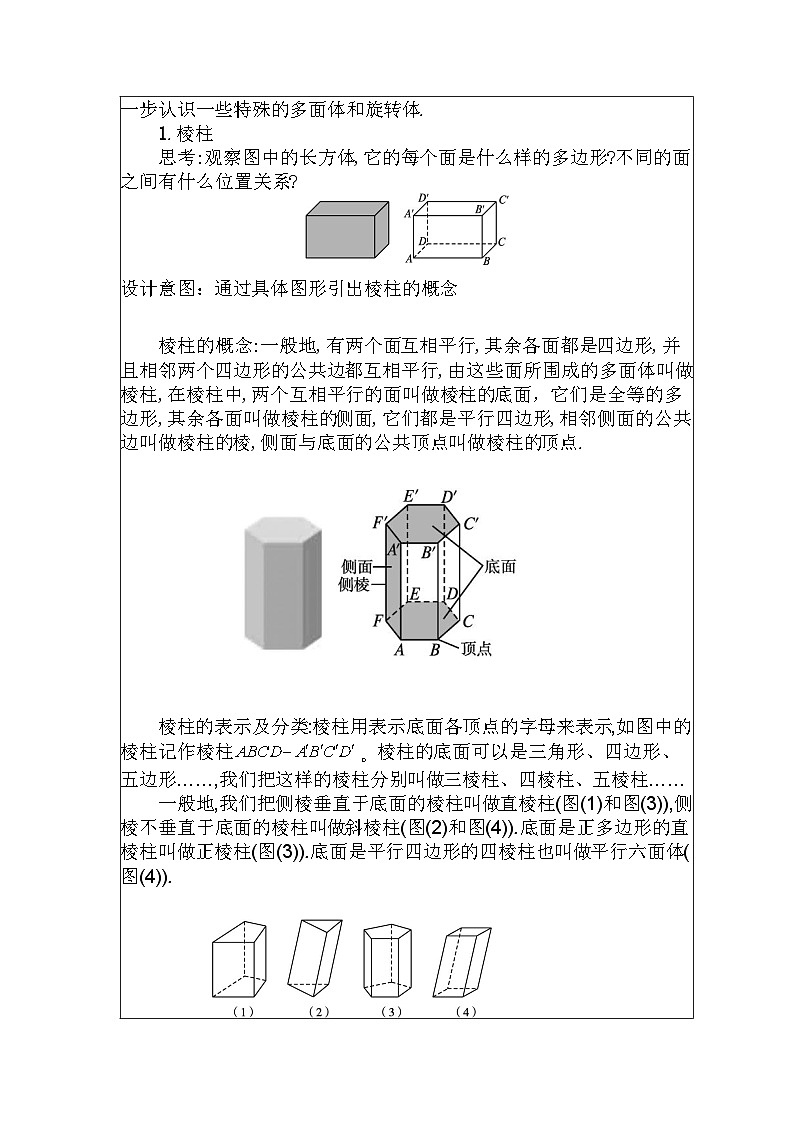
下面,我们从多面体和旋转体组成元素的形状、位置关系入手,进一步认识一些特殊的多面体和旋转体.

1.棱柱

思考:观察图中的长方体,它的每个面是什么样的多边形?不同的面之间有什么位置关系?

设计意图：通过具体图形引出棱柱的概念

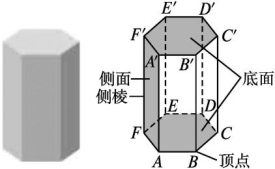
棱柱的概念:一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,在棱柱中,两个互相平行的面叫做棱柱的底面，它们是全等的多边形,其余各面叫做棱柱的侧面,它们都是平行四边形,相邻侧面的公共边叫做棱柱的棱,侧面与底面的公共顶点叫做棱柱的顶点. 

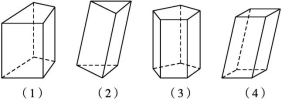
棱柱的表示及分类:棱柱用表示底面各顶点的字母来表示,如图中的棱柱记作棱柱。棱柱的底面可以是三角形、四边形、五边形……,我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱…… 

一般地,我们把侧棱垂直于底面的棱柱叫做直棱柱(图(1)和图(3)),侧棱不垂直于底面的棱柱叫做斜棱柱(图(2)和图(4)).底面是正多边形的直棱柱叫做正棱柱(图(3)).底面是平行四边形的四棱柱也叫做平行六面体(图(4)). 

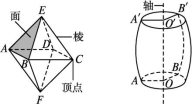
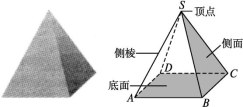
2.棱锥

棱锥的概念:一般地,有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.这个多边形面叫做棱锥的底面;有公共顶点的各个三角形面叫做棱锥的侧面;相邻侧面的公共边叫做棱锥的侧棱;各侧面的公共顶点叫做棱锥的顶点。 

棱锥的表示及分类:棱锥用表示顶点和底面各顶点的字母来表示,如图中的棱锥记作棱锥S-ABCD.棱锥的底面可以是三角形、四边形、五边形……,我们把这样的棱锥分别叫做三棱锥、四棱锥、五棱锥……,其中三棱锥又叫四面体.底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥. 

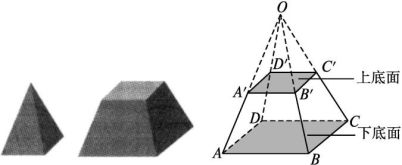
3.棱台

棱台的概念:如图所示,用一个平行棱锥底面的平面去截棱锥,我们把底面和截面之间那部分多面体叫做棱台.在棱台中,原棱锥的底面和截面分别叫做棱台的上底面和下底面.类似于棱柱、棱锥,棱台也有侧面、侧棱、顶点. 

棱台的表示及分类:棱台用表示底面各顶点的字母来表示,如图中的棱台记作棱台 .由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台…… 

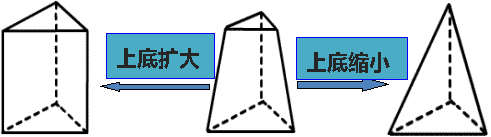
探究：棱柱、棱锥与棱台都是多面体，它们在结构上有哪些相同点和不同点？当底面发生变化时，它们能否互相转化？

设计意图：让学生直观的感受棱柱、棱锥、棱台之间的联系。

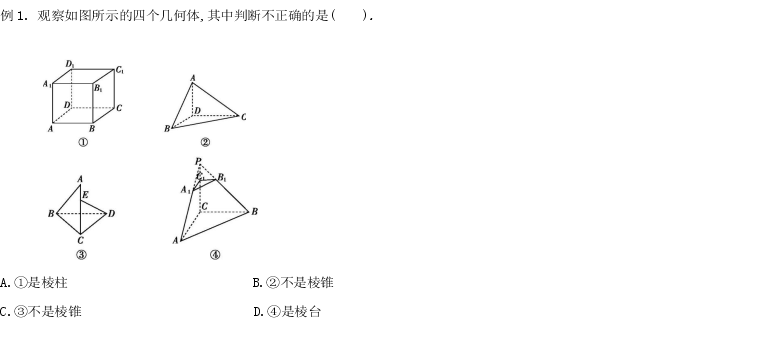
三．巩固练习

1.判断下列命题是否正确，正确的在括号内画 “√”，错误的画“×”．

（１）长方体是四棱柱，直四棱柱是长方体． （　　）

（２）四棱柱、四棱台、五棱锥都是六面体． （　　）

2.填空题

（１）一个几何体由７个面围成，其中两个面是互相平行且全等的五边形，其他各面都是全等的矩形， 则这个几何体是_________．

（２）一个多面体最少有________个面，此时这个多面体是_______.　

四．课堂小结

五．作业布置

课时分层（二十）