

2023八年级数学下册第十七章勾股定理测试卷(人教版附解析)
展开
这是一份2023八年级数学下册第十七章勾股定理测试卷(人教版附解析),共5页。
勾股定理一、选择题(每小题4分,共12分)1.如图,每个小正方形的边长为1,△ABC的三边a,b,c的大小关系是( ) A.a<c<b B.
A.a<c<b B.![]() a<b<
a<b<![]() cC.c<a<b D.c<b<a2.(2013·南京中考)设边长为3的正方形的对角线长为a,下列关
cC.c<a<b D.c<b<a2.(2013·南京中考)设边长为3的正方形的对角线长为a,下列关![]() 于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③3<a<4;④a是18的算术平方根.其中,所有正确说法的序号是( )A.①④ B.②③
于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③3<a<4;④a是18的算术平方根.其中,所有正确说法的序号是( )A.①④ B.②③ C.①②
C.①②![]() ④ D.①③④3.如图中的螺旋由一系列直角三角形组成,则第n个三角形的面积为( )A.n B.
④ D.①③④3.如图中的螺旋由一系列直角三角形组成,则第n个三角形的面积为( )A.n B.![]() C.
C.![]() D.
D.![]() 二、填空题(每小题4分,共12分)
二、填空题(每小题4分,共12分)![]() 4.如图所示,数轴上点A所表示的数为a,则a的值是 .
4.如图所示,数轴上点A所表示的数为a,则a的值是 .
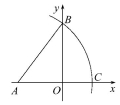 5.(2013·吉林中考)如图,在平面直角坐标系中,点A,B的坐标分别为(-6,0),(0,8).以点A为圆心,以AB长为半径画弧,交x正半轴于点C,则点C的坐标为 .6.如图是由4个边长为1的正方形构成的“田字格”.只用没有刻度的直尺在这个“田字格”中最多可以作出
5.(2013·吉林中考)如图,在平面直角坐标系中,点A,B的坐标分别为(-6,0),(0,8).以点A为圆心,以AB长为半径画弧,交x正半轴于点C,则点C的坐标为 .6.如图是由4个边长为1的正方形构成的“田字格”.只用没有刻度的直尺在这个“田字格”中最多可以作出![]() 长度为
长度为![]() 的线段 条.
的线段 条. 三、解答题(共26分)7.(8分)在同一直角坐标系中分别描出点A(-3,0),B(2,0),C(1,3),再用线段将这三点首尾顺次连接起来,求△ABC的面积与周长.
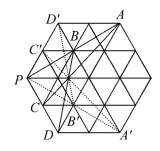
三、解答题(共26分)7.(8分)在同一直角坐标系中分别描出点A(-3,0),B(2,0),C(1,3),再用线段将这三点首尾顺次连接起来,求△ABC的面积与周长.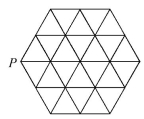 8.(8分)如图所示,在有24个边长为1的小正三角形的网格中,点P是正六边形的一个顶点,以点P为直角顶点作格点直角三角形,(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长.
8.(8分)如图所示,在有24个边长为1的小正三角形的网格中,点P是正六边形的一个顶点,以点P为直角顶点作格点直角三角形,(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长.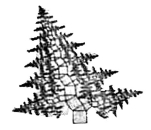 【拓展延伸】9.(10分)勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含30°角的直角三角形按一定规律长成的勾股树,树主干自下而上第一个正方形和第一个直角三角形的面积之和为S1,第二个正方形和第二个直角三角形的面积之和为S2,…,第n个正方形和第n个直角三角形的面积之和为Sn.设第一个正方形的边长为1.请解答下列问题:(1)S1= .(2)通过探究,用含n的式子表示Sn,则Sn= . 答案解析1.【解析】选C.∵AC=
【拓展延伸】9.(10分)勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含30°角的直角三角形按一定规律长成的勾股树,树主干自下而上第一个正方形和第一个直角三角形的面积之和为S1,第二个正方形和第二个直角三角形的面积之和为S2,…,第n个正方形和第n个直角三角形的面积之和为Sn.设第一个正方形的边长为1.请解答下列问题:(1)S1= .(2)通过探究,用含n的式子表示Sn,则Sn= . 答案解析1.【解析】选C.∵AC=![]() =5=
=5=![]() ,BC=
,BC=![]() =
=![]() ,AB=4=
,AB=4=![]() ,∴b>a>c,即c<a<b.2.【解析】选C.由勾股定理得,正方形的对角线长为a=
,∴b>a>c,即c<a<b.2.【解析】选C.由勾股定理得,正方形的对角线长为a=![]() =
=![]() =3
=3![]() ,且4<a<5.所以③错误,其他都正确.3.【解析】选D.根据勾股定理:在第一个三角形中:O
,且4<a<5.所以③错误,其他都正确.3.【解析】选D.根据勾股定理:在第一个三角形中:O![]() =1+1,S1=1×1÷2
=1+1,S1=1×1÷2![]() .在第二个三角形中:O
.在第二个三角形中:O![]() =O
=O![]() +1=1+1+1,S
+1=1+1+1,S![]() 2=OA1×1÷2=
2=OA1×1÷2=![]() ×1÷2.在第三个三角形中:O
×1÷2.在第三个三角形中:O![]() =O
=O![]() +1=1+1+1+1,S3=OA2×1÷2=
+1=1+1+1+1,S3=OA2×1÷2=![]() ×
×![]() 1÷2;…在第n个三角形中:Sn=
1÷2;…在第n个三角形中:Sn=![]() ×1÷2=
×1÷2=![]() .4.【解析】图中的直角三角形的两直角边为1和2,所以斜边长为
.4.【解析】图中的直角三角形的两直角边为1和2,所以斜边长为![]() =
=![]() ,所以-1到点A的距离是
,所以-1到点A的距离是![]() ,那么点A所表示的数为
,那么点A所表示的数为![]() -1.答案:
-1.答案:![]() -15.【解析】∵点A,B的坐标分别为(-6,0),(0,8),∴AO=6,BO=8,∴AB=
-15.【解析】∵点A,B的坐标分别为(-6,0),(0,8),∴AO=6,BO=8,∴AB=![]() =10,∵以点A为
=10,∵以点A为![]() 圆心,以AB长为半径画弧,∴AB=AC=10,∴OC=AC-AO=4,∵交x正半轴于点C,∴点C的坐标为(4,0).答案:(4,0)
圆心,以AB长为半径画弧,∴AB=AC=10,∴OC=AC-AO=4,∵交x正半轴于点C,∴点C的坐标为(4,0).答案:(4,0) 6.【解析】如图,由于每个小正方形的边长都为1,那么根据勾股定理容易得到长度为
6.【解析】如图,由于每个小正方形的边长都为1,那么根据勾股定理容易得到长度为![]() 的线段,然后可以找出所有这样的线段.如图,所有长度为
的线段,然后可以找出所有这样的线段.如图,所有长度为![]() 的线段全部画出,共有8条.答案:87.【解析】如图,利用勾股定理得,AC=
的线段全部画出,共有8条.答案:87.【解析】如图,利用勾股定理得,AC=![]() =5,BC
=5,BC![]() =
=![]() =
=![]()
![]() ,AB=2-(-3)=5,
,AB=2-(-3)=5,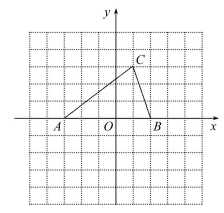 ∴△ABC的周长为A
∴△ABC的周长为A![]() C+BC+AB=5+
C+BC+AB=5+![]() +5=10+
+5=10+![]() ,面积为
,面积为![]() ×5×3=
×5×3=![]() .8.【解析】通过作图知,以点P为直角的三角形有八种情况,如图,△PCB,△PCA,△PDB,△PDA,△PC'B',△PC'A',△PD'B',△PD'A',均是以点P为直角的直角三角形,且△PCB≌△PC'B',△PCA≌△PC'A',△PDB≌△PD'B',△PDA≌△PD'A',故:在Rt△PCB中,BC=
.8.【解析】通过作图知,以点P为直角的三角形有八种情况,如图,△PCB,△PCA,△PDB,△PDA,△PC'B',△PC'A',△PD'B',△PD'A',均是以点P为直角的直角三角形,且△PCB≌△PC'B',△PCA≌△PC'A',△PDB≌△PD'B',△PDA≌△PD'A',故:在Rt△PCB中,BC=![]() =
=![]() =2=B'C';在Rt△PCA中,AC=
=2=B'C';在Rt△PCA中,AC=![]() =
=![]() =
=![]() =A'C';在Rt△PDB中,BD=
=A'C';在Rt△PDB中,BD=![]() =
=![]() =
=![]() =B'D';在Rt△PDA中,AD=
=B'D';在Rt△PDA中,AD=![]() =
=![]() =4=A'D'.故所有可能的直角三角形斜边的长为4,2,
=4=A'D'.故所有可能的直角三角形斜边的长为4,2,![]() ,
,![]() .
. 9.【解析】(1)∵第一个正方形的边长为1,∴正方形的面积为1,又∵直角三角形一个角为30°,∴三角形的一条直角边为
9.【解析】(1)∵第一个正方形的边长为1,∴正方形的面积为1,又∵直角三角形一个角为30°,∴三角形的一条直角边为![]() ,另一条直角边就是
,另一条直角边就是![]() =
=![]() ,∴三角形的面积为
,∴三角形的面积为![]() ×
×![]() ÷2=
÷2=![]() ,∴S
,∴S![]() 1=1+
1=1+![]() .(2)∵第二个正方形的边长为
.(2)∵第二个正方形的边长为![]() ,它的面积就是
,它的面积就是![]() ,也就是第一个正方形面积的
,也就是第一个正方形面积的![]() ,同理,第二个三角形的面积也是第一个三角形的面积的
,同理,第二个三角形的面积也是第一个三角形的面积的![]() ,∴S2=
,∴S2=![]() ·
·![]() ,依此类推,S3=
,依此类推,S3=![]() ·
·![]() ·
·![]() ,即S3=
,即S3=![]() ·
·![]()
![]() ,所以Sn=
,所以Sn=![]() ·
·![]() (n为整数).
(n为整数).






