
高中8.5 空间直线、平面的平行教案设计
展开8.5 空间直线、平面的平行
8.5.2 直线与平面平行
教学设计
一、教学目标
1.理解并掌握直线与平面平行的判定定理以及性质定理.
2.掌握由线线平行证明线面平行以及由线面平行推出线线平行.
3.能运用定理证明一些空间位置关系的简单命题.
二、教学重难点
1、教学重点
直线与平面平行的判定定理和性质定理.
2、教学难点
直线与平面平行的判定定理和性质定理及其应用.
三、教学过程
1、新课导入
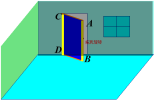 1、在门扇的旋转过程中,AB、CD和门框所在平面三者之间有什么关系?
1、在门扇的旋转过程中,AB、CD和门框所在平面三者之间有什么关系?
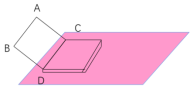 2、将一本书平放在桌面上,翻动书的封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?
2、将一本书平放在桌面上,翻动书的封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?
2、探索新知
1.直线与平面平行的判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
符号表示:a⊄α,b⊂α,且a∥b⇒a∥α.
图形表示: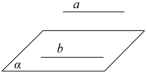
例1 求证:空间四边形相邻两边中点的连线平行于经过另外两边的平面.
已知:如图,空间四边形![]() 中,E,F分别是
中,E,F分别是![]() ,
,![]() 的中点.
的中点.
求证:EF//平面BCD.
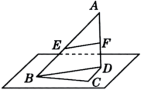
证明:连接BD.
![]() ,
,![]()
![]() .
.
又![]() 平面BCD,
平面BCD,![]() 平面BCD,
平面BCD,
![]() 平面BCD.
平面BCD.
2.直线与平面平行的性质定理:一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.
符号表示:若a∥α,a⊂β,α∩β=b,则a∥b.
图形表示: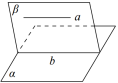
例2 如图所示的一块木料中,棱BC平行于面![]() .
.
(1)要经过面![]() 内的一点P和棱BC将木料锯开,在木料表面应该怎样画线?
内的一点P和棱BC将木料锯开,在木料表面应该怎样画线?
(2)所画的线与平面AC是什么位置关系?
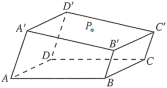
分析:要经过面![]() 内的一点P和棱BC将木料锯开,实际上是经过BC及BC外一点P作截面,也就需要找出所作的截面与相关平面的交线. 我们可以依据直线与平面平行的性质定理、基本事实4和推论1画出所需要的线段.
内的一点P和棱BC将木料锯开,实际上是经过BC及BC外一点P作截面,也就需要找出所作的截面与相关平面的交线. 我们可以依据直线与平面平行的性质定理、基本事实4和推论1画出所需要的线段.
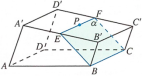
解:(1)如图,在平面![]() 内,过点P作直线EF,使
内,过点P作直线EF,使![]() ,并分别交棱
,并分别交棱![]() ,
,![]() 于点E,F,连接BE,CF,则EF,BE,CF就是应画的线.
于点E,F,连接BE,CF,则EF,BE,CF就是应画的线.
(2)因为棱BC平行于平面![]() ,平面
,平面![]() 与平面
与平面![]() 相交于
相交于![]() ,
,
所以![]() ,
,
由(1)知,![]() ,所以
,所以![]() ,
,
而BC在平面AC内,EF在平面AC外,
所以![]() 平面AC,
平面AC,
显然,BE,CF都与平面AC相交.
3、小结作业
小结:本节课学习了直线与平面平行的判定定理和性质定理及其应用.
作业:完成本节课课后习题.
四、板书设计
8.5.2 直线与平面平行
1.直线与平面平行的判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
符号表示:a⊄α,b⊂α,且a∥b⇒a∥α.
图形表示: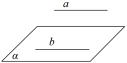
2.直线与平面平行的性质定理:一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.
符号表示若a∥α,a⊂β,α∩β=b,则a∥b.
图形表示: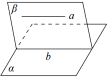
高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行精品教案: 这是一份高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行精品教案,共7页。
人教A版 (2019)必修 第二册8.5 空间直线、平面的平行教学设计: 这是一份人教A版 (2019)必修 第二册8.5 空间直线、平面的平行教学设计,共11页。
数学必修 第二册8.5 空间直线、平面的平行教案: 这是一份数学必修 第二册8.5 空间直线、平面的平行教案,共5页。教案主要包含了预习课本,引入新课,新知探究,典例分析,直线与平面平行的判定定理的应用,课堂小结,板书设计,作业等内容,欢迎下载使用。













