2022-2023学年重庆市大渡口区七年级（下）期末数学试卷-普通用卷

这是一份2022-2023学年重庆市大渡口区七年级（下）期末数学试卷-普通用卷，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 计算(x2)3的结果是( )
A. x5B. x6C. x8D. 3x2
2. 下面的数字图案，不是轴对称图形的是( )
A. B. C. D.
3. 从某班学生中随机选取一名学生是女生的概率为35，则该班女生与男生的人数比是( )
A. 32B. 35C. 23D. 25
4. 已知三角形两边长分别为7、11，那么第三边的长可以是( )
A. 2B. 3C. 4D. 5
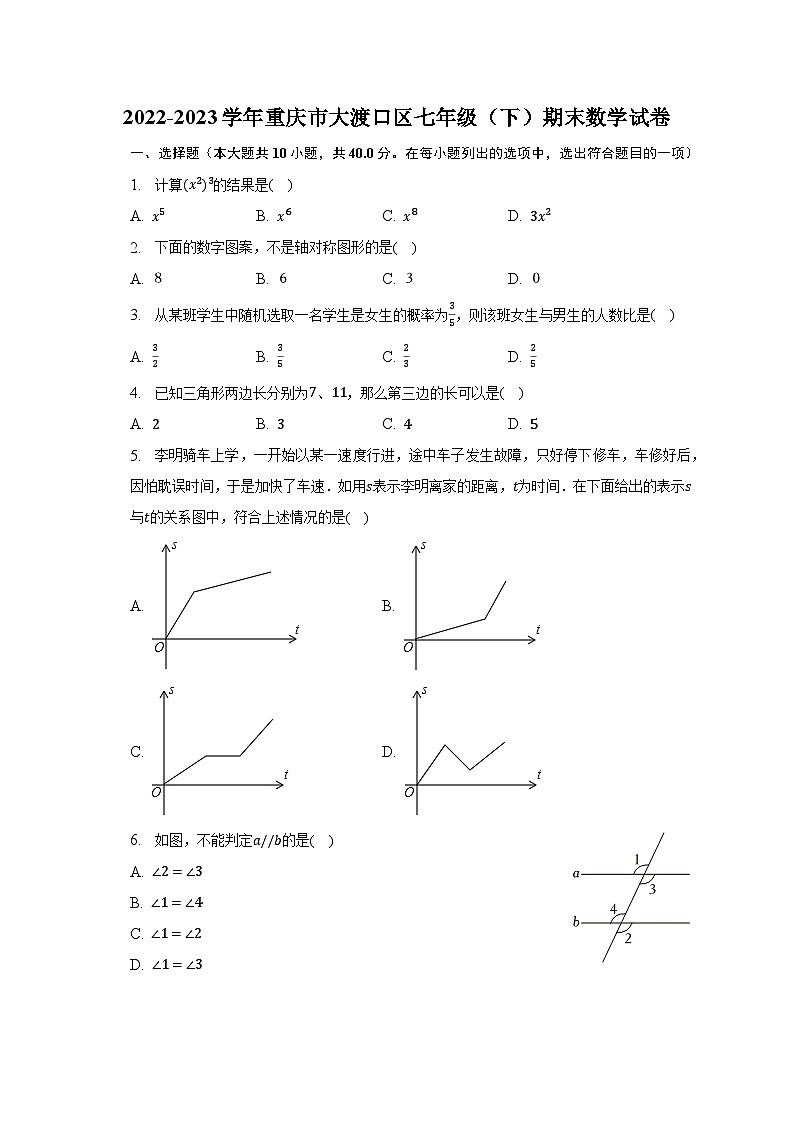
5. 李明骑车上学，一开始以某一速度行进，途中车子发生故障，只好停下修车，车修好后，因怕耽误时间，于是加快了车速．如用s表示李明离家的距离，t为时间．在下面给出的表示s与t的关系图中，符合上述情况的是( )
A. B.
C. D.
6. 如图，不能判定a//b的是( )
A. ∠2=∠3
B. ∠1=∠4
C. ∠1=∠2
D. ∠1=∠3
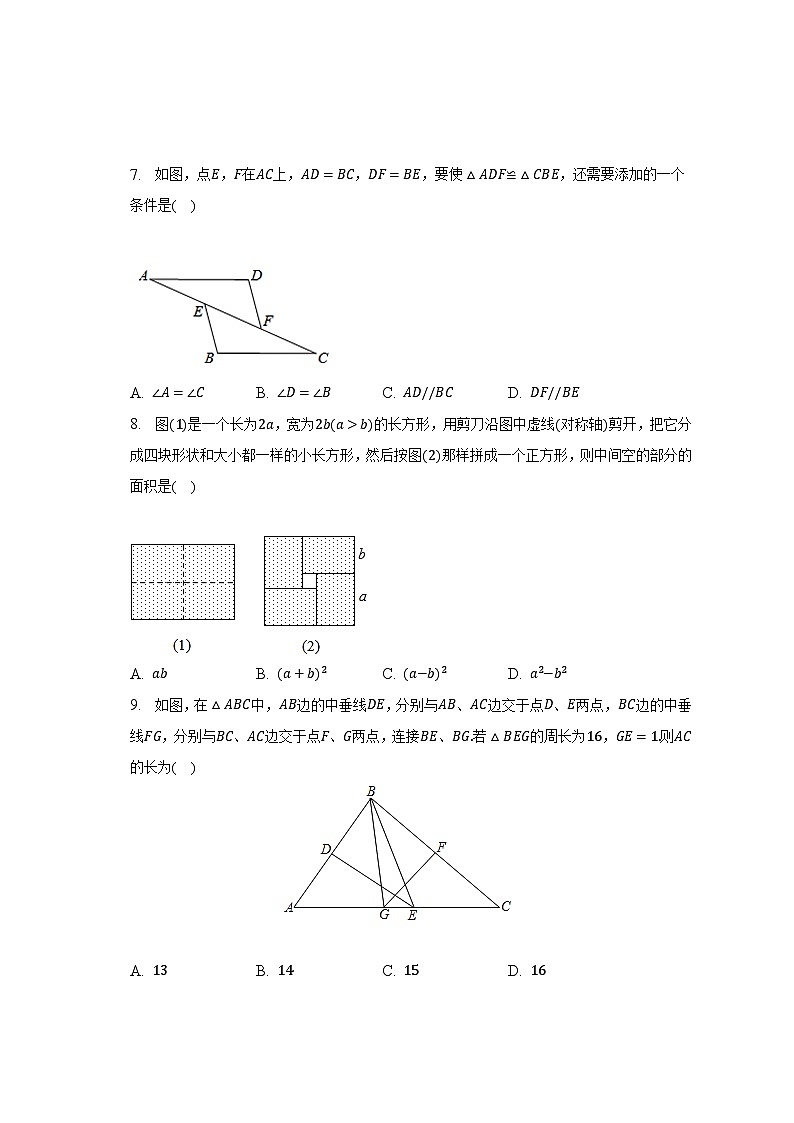
7. 如图，点E，F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加的一个条件是( )
A. ∠A=∠CB. ∠D=∠BC. AD//BCD. DF//BE
8. 图(1)是一个长为2a，宽为2b(a>b)的长方形，用剪刀沿图中虚线(对称轴)剪开，把它分成四块形状和大小都一样的小长方形，然后按图(2)那样拼成一个正方形，则中间空的部分的面积是( )
A. abB. (a+b)2C. (a−b)2D. a2−b2
9. 如图，在△ABC中，AB边的中垂线DE，分别与AB、AC边交于点D、E两点，BC边的中垂线FG，分别与BC、AC边交于点F、G两点，连接BE、BG.若△BEG的周长为16，GE=1.则AC的长为( )
A. 13B. 14C. 15D. 16
10. 如果10b=n，那么b为n的劳格数，记为d(n)=b，例如101=10，d(10)=1，则下列说法正确的个数是( )
①d(10−2)=−2；
②d(a3)d(a)=3；
③若d(2)=0.301，则d(16)=1.204．
A. 0B. 1C. 2D. 3
二、填空题（本大题共8小题，共32.0分）
11. 一种细胞的直径约为0.00065米，将0.00065用科学记数法表示为______ ．
12. 已知∠β=52°，则∠β的余角的度数为______°.
13. 在一只不透明的口袋中放入只有颜色不同的白球7个，黑球5个，黄球n个，搅匀后随机从中摸取一个恰好是黄球的概率为13，则放入的黄球总数n= ______ ．
14. 如图，在Rt△ABC中，∠ACB=90°，BD平分∠ABC，DE⊥AB于点E，AC=9，AD=5，则DE的长为______ ．
15. 如图，在Rt△ABC中，∠A=90°，点E，F分别为AB，AC上一点，将△ABC沿直线EF翻折至同一平面内，点A落在点A′处，EA′，FA′分别交BC边于点M，N.若∠BEA′=80°，则∠CFA′的度数为______ ．
16. 已知x2+2(m+1)x+25是完全平方式，则m的值为______．
17. 如图，在△ABC中，G是边BC上任意一点，D、E、F分别是AG、BD、CE的中点，S△ABC=40，则S△DEF= ______ ．
18. 对任意一个三位正整数m=abc−(1≤a≤9,1≤b≤9,1≤c≤9,a,b,c且均为正整数)，如果m满足各个数位上的数字均不相同，且三个数位上的数字之和不小于10，则称这个数为“超级数”.现将一个“超级数”规定F(m)=|a−c|.例如：a=263，因为2，6，3均不相等，且2+6+3=11>10，所以263是超级数，F(263)=|2−3|=1.请计算F(356)的值______ ；若s，t都是“超级数”，其中s=140+x，t=100y+85(1≤x≤9,1≤y≤9,x,y且均为正整数)，规定：K=t−s，若F(s)+F(t)=6，则K的最大值与最小值的和是______ ．
三、解答题（本大题共8小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题8.0分)
(1)2−2+(π−3)0+(1−2)233；
(2)(−3x2y)2⋅(2xy2)÷(6x3y3).
20. (本小题10.0分)
如图，AD//BC，∠B+∠BCD=180°
(1)用直尺和圆规完成以下基本作图：过点A作∠BAD的角平分线，交CD于点F，与BC的延长线交于点E；(不写作法，保留作图痕迹)
(2)求证：∠CFE=∠FEC．
证明：∵AD//BC(已知)，
∴∠DAF=∠FEC(①______ ).
∵AE平分∠BAD，
∴② ______ (角平分线的定义)．
∴∠BAE=∠FEC(③______ ).
∵∠B+∠BCD=180°(已知)，
∴④ ______ (⑤______ ).
∴∠BAE=∠CFE(两直线平行，同位角相等)．
∴∠CFE=∠FEC(等量代换)．
21. (本小题10.0分)
先化简，再求值：[(a+2b)2−(a+b)(a−b)−3b2]÷(2b)，其中a=−1,b=12．
22. (本小题10.0分)
新型冠状病毒爆发，教育部部署了“停课不停学”的有关工作，各地都在进行在线教育．小依同学为了了解网课学习情况，对本班部分同学最喜爱的课程进行了调查，调查课程分别是网上授课、体育锻炼、名著阅读、艺术欣赏和其他课程并制成以下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：
(1)本次调查中一共调查了______名学生，其中“名著阅读”所占的圆心角度数为______．
(2)请把条形统计图补全．
(3)在调查的同学中随机选取一名学生，求他恰好最喜爱的课程是“艺术欣赏”的概率．
(4)若该校一共有3000名学生，请估算出全校最喜爱的课程是“体育锻炼”的人数．
23. (本小题10.0分)
如图，方格纸中每一个小正方形的边长都是1，在方格纸内将△ABC经过一次轴对称变换后得到△A′B′C′，图中标出了点C的对应点C′．
(1)作出△ABC与△A′B′C′关于直线MN对称的对称轴MN；
(2)在给定的方格纸中画出变换后的△A′B′C；
(3)若方格纸的格点上存在一点P(异于点C)，使S△ABP=S△ABC，作出符合条件的点P(不包括方格纸的边框)．
24. (本小题10.0分)
如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF//AB，交ED的延长线于点F．
(1)求证：△BDE≌△CDF；
(2)当AD⊥BC，AE=2，CF=1时，求AC的长．
25. (本小题10.0分)
如图1，在长方形ABCD中，点P为长方形边上一动点，点P以每秒v cm的速度从B−C−D的路径匀速移动，移动到D处后以每秒2v cm的速度从D−A的路径匀速移动，运动到点A时停止.在整个移动的过程中，设点P移动的时间为t秒，点P到AB的距离为y cm，时间t与距离y的关系图象如图2所示.若AB=6cm，根据图象信息回答下列问题：

(1)线段BC= ______ cm，v= ______ cm/s；
(2)图2中a的值是______ ；
(3)当y=8cm时，求移动时间t的值．
26. (本小题10.0分)
在△ABC和△AEF中AC=AE，连接CE，CE恰好平分∠ACB，在CE上存在一点D，使∠DAF与∠ACB互为补角，连接AD．

(1)如图1，当∠ACB=60°时，求∠CAE的度数；
(2)如图2，当∠ACB=120°，AD=AF时，试说明EF与AC的位置关系；
(3)在(2)问的条件下，如图3连接FD并延长，分别交BC，AE于点M，N，若MN=4，AC=BC，P，Q分别为AB和AE上的动点，请直接写出△DPQ周长的最小值．
答案和解析
1.【答案】B
【解析】解：(x2)3=x6．
故选B．
根据幂的乘方和积的乘方的运算法则求解．
本题考查了幂的乘方和积的乘方，解答本题的关键是掌握幂的乘方和积的乘方的运算法则．
2.【答案】B
【解析】解：数字图案中，不是轴对称图形的是6．
故选：B．
如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，由此即可判断．
本题考查轴对称图形，关键是掌握轴对称图形的定义．
3.【答案】A
【解析】解：女生占全班5份中的3份，所以男生就是占(5−3)=2份，所以女生与男生的人数比是32．
故选A．
先求出男生所占全班同学的份数，再求出女生与男生的人数比即可．
此题主要考查概率的意义及求法；易错点是得到该班男生占全班同学的份数．
4.【答案】D
【解析】
【分析】
此题主要考查了三角形的三边关系，关键是掌握三角形三边关系为任意两边之和大于第三边，任意两边之差小于第三边．根据三角形的三边关系可得11−7