北师大版数学八年级上册课件第六章 数据的分析

这是一份北师大版数学八年级上册课件第六章 数据的分析，共13页。
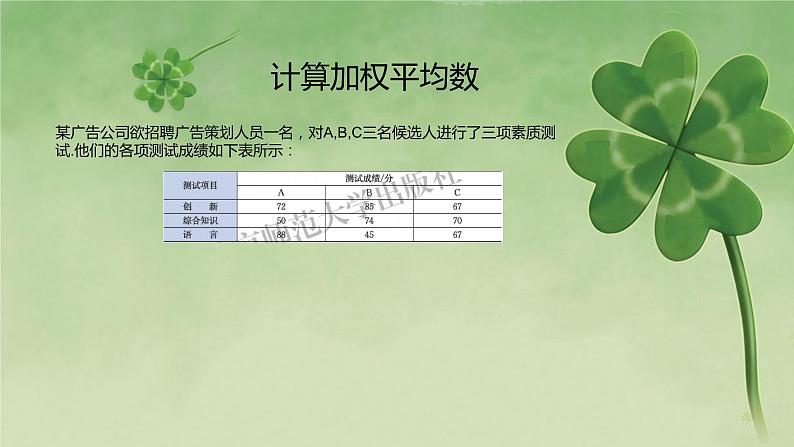
第六章 数据的分析初二北师大版上册在日常生活中，我们常用平均数描述一组数据的集中趋势.一般地，对于n个数x1,x₂,…,xn,我们把1/n(x₁+x₂+…+xn,)叫做这n个数的算术平均数,简称平均数，记为x.算术平均数-例如，求一次考试班里同学的平均分、计算生活费时求一个月每天平均的花销等，都是平均数。北京金隅队队员的年龄分布如下，请计算该球队的平均年龄：解：平均年龄=(19×1+22×4+23×2+26×2+27×1+28×2+29×2+35×1)÷(1+4+2+2+1+2+2+1)=25.4(岁).计算平均数年龄是指数据（X1,X2,X3......Xn），相应年龄对应的人数是数据的个数。按大小顺序排列为：19，22，22，22，22，23，23......35。在这道题中，n是所有队员的数量。总人数，也就是n以22为例，22岁有4名队员，则在这组数据里就有4个 22.某广告公司欲招聘广告策划人员一名，对A,B,C三名候选人进行了三项素质测试.他们的各项测试成绩如下表所示：计算加权平均数(2)根据实际需要，公司将创新、综合知识和语言三项测试得分按4:3:1的比例确定各人的测试成绩，此时谁将被录用?实际问题中，一组数据里的各个数据的“重要程度”未必相同.因而，在计算这组数据的平均数时，往往给每个数据一个“权”.例如，题中4,3,1分别是创新、综合知识、语言三项测试成绩的权。代入权所得结果即为加权平均数。计算加权平均数权之和一般地，n个数据按大小顺序排列，处于最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.一组数据中出现次数最多的那个数据叫做这组数据的众数.如一组数据1.5,1.5,1.6,1.65,1.7,1.7,1.75,1.8的中位数是1/2(1.65+1.7),即1.675;众数是1.5和1.7.中位数与众数这组数据共8个，分为两组，第一组的最后一个数据是第四位，第二组的第一个数据是第五位，则，第四和第五位数据就是最中间的两个数，求二者之平均数即为中位数。平均数、中位数和众数都是描述数据集中趋势的统计量.计算平均数时，所有数据都参加运算，它能充分地利用数据所提供的信息，因此在现实生活中较为常用，但它容易受极端值的影响.如体操比赛评分时，个别裁判不公正打分将直接影响运动员的成绩.为此一般先去掉一个最高分和一个最低分，然后求其余得分的平均数作为运动员的得分.中位数的优点是计算简单，受极端值影响较小，但不能充分利用所有数据的信息.一组数据中某些数据多次重复出现时，众数往往是人们尤为关心的一个量.如选举，就是选择名字出现次数最多的那个人，因而可以将当选者的名字当做“众数”.但各个数据的重复次数大致相等时，众数往往没有特别意义.三者的特点甲、乙、丙三支青年排球队各有12名队员，三队队员的年龄情况如图.从统计图分析数据的集中趋势(1)观察图6-2,你能从图中分别看出三支球队队员年龄的众数吗?中位数呢?(2)根据图6-2,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?(3)计算出三支球队队员的平均年龄，看看你的估计是否准确.从统计图分析数据的集中趋势（1）众数看条柱最高的数，中位数看第6和第7位。众数：甲20 乙19 丙21 中位数：甲20 乙19 丙21（2）中位数相同时，一般看众数，估计丙队平均年龄最大，乙队平均年龄最小。（3）甲 20 乙19.3 丙20.6数据离散程度观察两张图，数据的离散程度如何？乙厂的数据比甲厂分散。数学上，数据的离散程度还可以用方差或标准差刻画，方差是各个数据与平均数差的平方的平均数，即数据的离散程度，即它们相对于集中趋势的偏离情况.一组数据中最大数据与最小数据的差(称为极差),就是刻画数据离散程度的一个统计量.刻画离散程度其中，x是x₁,x₂,…,xn的平均数，s²是方差，而标准差就是方差的算术平方根.一般而言，一组数据的极差、方差或标准差越小，这组数据就越稳定.刻画离散程度－END