新教材2023版高中数学第七章三角函数7.1任意角的概念与蝗制7.1.2蝗制及其与角度制的换算课件新人教B版必修第三册

这是一份新教材2023版高中数学第七章三角函数7.1任意角的概念与蝗制7.1.2蝗制及其与角度制的换算课件新人教B版必修第三册，共37页。

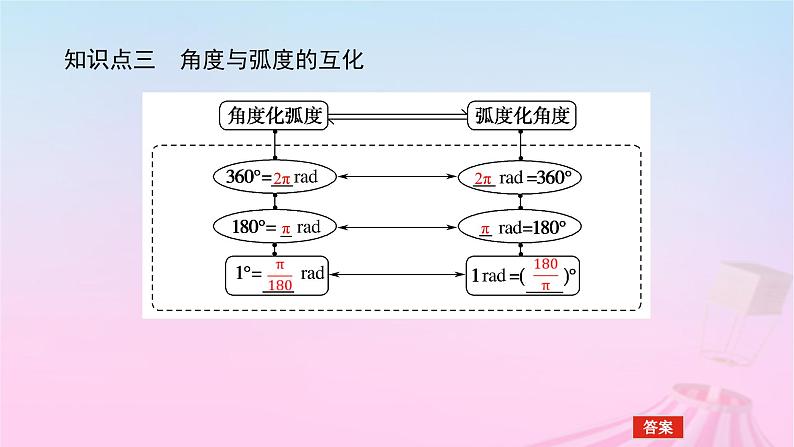
7．1.2　弧度制及其与角度制的换算新知初探·自主学习课堂探究·素养提升【课程标准】了解任意角的概念和弧度制，能进行弧度与角度的互化，体会引入弧度制的必要性．新知初探·自主学习教 材 要 点知识点一　角度制与弧度制的定义(1)角度制：用度作单位来度量角的制度称为________.角度制规定60分等于1度，60秒等于1分．(2)弧度制：长度等于________的圆弧所对的________为1弧度的角，记作________．以________为单位来度量角的制度称为弧度制．知识点二　角的弧度数的计算在半径为r的圆中，弧长为l的弧所对圆心角为α rad，则|α|＝_____．角度制半径长圆心角1 rad弧度 知识点三　角度与弧度的互化2π2πππ  知识点四　一些特殊角与弧度数的对应关系0       π   2π知识点五　扇形的弧长与面积公式设扇形的半径为r，弧长为l，α为其圆心角，则 αr     答案：D解析：1 080°＝180°×6，所以1 080°化为弧度是6π. 答案：C  6π 课堂探究·素养提升 【答案】　D【解析】　根据角度和弧度的定义，可知无论是角度制还是弧度制，角的大小与圆的半径长短无关，而是与弧长与半径的比值有关，所以D项是假命题，A、B、C三项均为真命题．由题目可获取以下主要信息：各选项中均涉及到角度与弧度，解答本题可从角度和弧度的定义着手．(2)用弧度表示终边落在阴影部分内(不包括边界)的角的集合．   方法归纳弧度制与角度制的区别与联系跟踪训练1　(1)下列各说法中，错误的是(　　)A．半圆所对的圆心角是π radB．周角的大小等于2πC．1弧度的圆心角所对的弧长等于该圆的半径D．长度等于半径的弦所对的圆心角的大小是1弧度答案：D解析：由弧度的定义知，弧长等于半径的圆弧所对的圆心角即为一弧度的角，易知ABC正确．D中长度等于半径的弧所对的圆心角的大小为1弧度，故D错误． 答案：A     跟踪训练2　用弧度表示终边落在如图所示阴影部分内(不包括边界)的角θ的集合．  教材反思角度制与弧度制的比较题型3　弧长公式与扇形面积公式的应用例3　(1)已知扇形的半径为10 cm，圆心角为60°，求扇形的弧长和面积； 状元随笔　已知扇形的半径、圆心角， 把圆心角化为弧度制，利用扇形的弧长、面积公式算出即可．(2)设扇形的周长为8 cm，面积为4 cm2，则扇形的圆心角的弧度数是(　　)A．1 rad B．2 radC．3 rad D．4 rad可由扇形周长和面积建立方程组，通过解方程组求得．【答案】　B (3)已知扇形的周长为20 cm，当它的半径和圆心角各取什么值时，才能使扇形的面积最大？最大面积是多少？可通过建立扇形面积的目标函数来求解． 跟踪训练3　(1)如果一扇形的圆心角为60°，半径等于3 cm，则该扇形的弧长为________cm，面积为________cm2;  π (2)(变条件)用30 cm长的铁丝围成一个扇形，应怎样设计才能使扇形的面积最大？最大面积是多少？