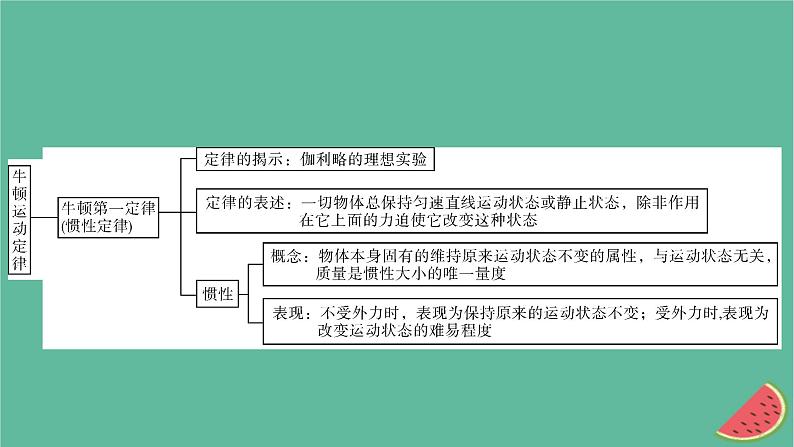
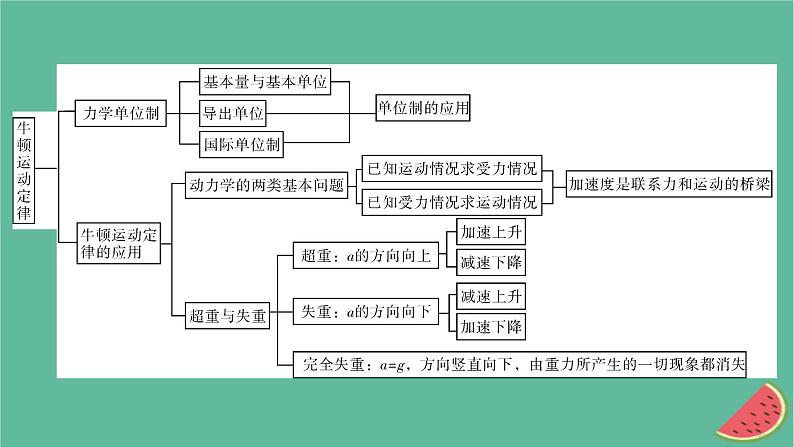
2023年新教材高中物理本章小结4第4章牛顿运动定律课件粤教版必修第一册

这是一份2023年新教材高中物理本章小结4第4章牛顿运动定律课件粤教版必修第一册，共58页。
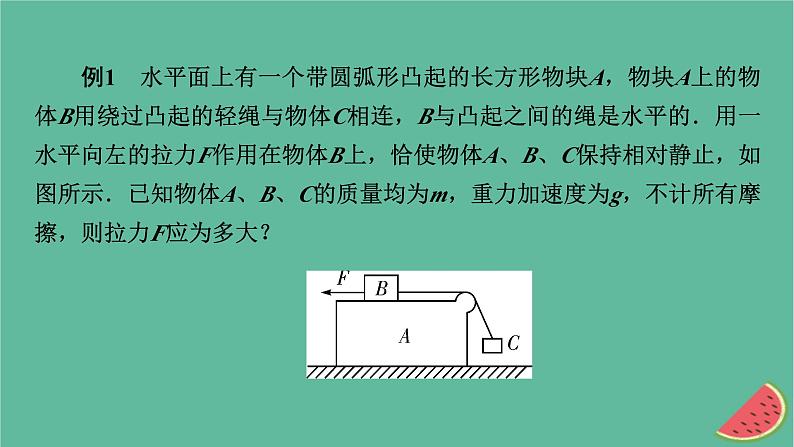
第四章　牛顿运动定律本章小结构建知识网络归纳专题小结专题1　整体法和隔离法的应用整体法和隔离法是在解决平衡问题、连接体问题及多个物体的动力学问题时经常遇到的解题方法．对于连接体问题，若将连接体作为整体，则不必分析连接体之间的相互作用，只需分析外界对连接体的作用力，从而简化受力过程，加快解题速度．若求解连接体之间的相互作用力，则必须将物体隔离出来，化内力为外力，才能求解．但要注意此类问题用整体法时必须是相互作用的物体具有相同的加速度．在一些问题中，隔离法和整体法经常交替使用．例1　水平面上有一个带圆弧形凸起的长方形物块A，物块A上的物体B用绕过凸起的轻绳与物体C相连，B与凸起之间的绳是水平的．用一水平向左的拉力F作用在物体B上，恰使物体A、B、C保持相对静止，如图所示．已知物体A、B、C的质量均为m，重力加速度为g，不计所有摩擦，则拉力F应为多大？解析：设绳中张力大小为T，A、B、C共同的加速度为a，与C相连部分的绳与竖直方向的夹角为α，如图所示．由牛顿运动定律对A、B、C组成的整体进行分析，有F＝3ma， ①对B有F－T＝ma， ②对C有Tcos α＝mg， ③Tsin α＝ma， ④联立①②式得T＝2ma， ⑤联立③④式得T2＝m2(a2＋g2)， ⑥专题2　牛顿第二定律与图像综合问题例2　如图甲所示，静止在光滑水平面上的长木板B(长木板足够长)的右端放着小物块A，某时刻B受到水平向右的外力F作用，F随时间t的变化规律如图乙所示，即F＝kt，其中k为已知常数．若物体之间的滑动摩擦力F的大小等于最大静摩擦力，且A、B的质量相等，则图中可以定性地描述物块A的v－t图像的是 (　　)答案：B例3　如图所示，水平传送带以速度v1匀速运动，小物体P、Q由通过定滑轮且不可伸长的轻绳相连，t＝0时刻P在传送带左端具有速度v2，P与定滑轮间的绳水平，t＝t0时刻P离开传送带．不计定滑轮质量和摩擦，绳足够长．图中正确描述小物体P速度随时间的变化曲线可能是 (　　)解析：若v2μmPg，满足mQg＋μmPg＝(mP＋mQ)a2，则P中途减速至v1，以后满足mQg－μmPg＝(mP＋mQ)a3，以a3先减速到0再以相同的加速度返回直到离开传送带(也可能减速过程中就离开传送带)，C正确，A、D错误．答案：BC专题3　用程序法求解动力学综合问题程序法：按时间的先后顺序对题目给出的物体的运动过程(或不同的状态)进行分析(包括列式计算)的解题方法称为程序法．程序法解题的基本思路：(1)划分出题目中有多少个不同过程或多少个不同状态；(2)对各个过程或各个状态进行受力情况和运动情况的分析并得出正确的结果；(3)前一个过程的结束就是后一个过程的开始，两个过程的交接点往往是求解问题的关键；(4)对相互关联的两个(或两个以上)运动对象，应分别研究，然后找出其关联方程，如时间关系、空间关系、速度关系等．例4　一个长木板置于粗糙水平地面上，木板左端放置一个小物块，在木板右方有一面墙壁，木板右端与墙壁的距离为4.5 m，如图甲所示．从t＝0时刻开始，小物块与木板一起以共同的速度向右运动，直至t＝1 s时木板与墙壁碰撞(碰撞时间极短)．碰撞前后木板速度的大小不变，方向相反，运动过程中小物块始终未离开木板．已知碰撞后1 s内小物块的v－t图像如图乙所示．木板的质量是小物块质量的15倍，g取10 m/s2.求：(1)木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2；(2)木板的最小长度；(3)木板右端离墙壁的最终距离．解析：(1)规定向右为正方向．木板与墙壁相碰前，小物块和木板一起向右做匀变速运动，设加速度为a1，小物块和木板的质量分别为m和M.由牛顿第二定律，有－μ1(m＋M)g＝(m＋M)a1. ①由图乙可知，木板与墙壁碰前瞬间的速度v1＝4 m/s，由运动学公式，得v1＝v0＋a1t1， ②式中t1＝1 s，s0＝4.5 m，v0是小物块和木板开始运动时的速度．联立①②③式并结合题给条件解得μ1＝0.1. ④在木板与墙壁碰撞后，木板以－v1的初速度向左做匀变速运动，小物块以v1的初速度向右做匀变速运动．设小物块的加速度为a2，由牛顿第二定律，有－μ2mg＝ma2， ⑤式中t2＝2 s，v2＝0，联立⑤⑥式并结合题给条件，得μ2＝0.4. ⑦(2)设碰撞后木板的加速度为a3，经过时间Δt，木板和小物块刚好具有共同的速度v3.由牛顿第二定律及运动学公式，得μ2mg＋μ1(M＋m)g＝Ma3， ⑧v3＝－v1＋a3Δt， ⑨v3＝v1＋a2Δt， ⑩碰撞后至木板和小物块刚好达到共同速度的过程中，木板的位移小物块相对木板的位移为Δs＝s2－s1， ⑬联立⑥⑧～⑬式，并代入数据得Δs＝6.0 m． ⑭因为运动过程中小物块没有脱离木板，所以木板的最小长度应为6.0 m.(3)在小物块和木板具有共同的速度后，两者向左做匀变速运动直至停止．设加速度为a4，此过程中小物块和木板运动的位移为s3.由牛顿第二定律及运动学公式，得μ1(m＋M)g＝(m＋M)a4， ⑮碰后木板的位移s＝s1＋s3， ⑰联立⑥⑧⑨⑩⑪⑮⑯⑰式，并代入数据得s＝－6.5 m.木板右端离墙壁的最终距离为6.5 m.专题4　临界、极值问题的分析求解1．动力学中的典型临界问题的临界条件．(1)接触与脱离的临界条件：弹力FN＝0.(2)发生相对滑动的临界条件：静摩擦力达到最大值．(3)绳子断裂的临界条件：绝对张力等于绳子所能承受的最大张力．(4)绳子松弛的临界条件：绳子的张力FT＝0.(5)加速度最大的临界条件：合力最大．(6)速度最大的临界条件：加速度为零．2．研究平衡物体的极值问题的常用方法．(1)物理分析法：通过对物理过程的分析，抓住临界(或极值)条件进行求解．(2)解析法：根据物体的平衡条件列方程，写出物理量之间的函数关系，在解方程时采用数学知识求极值，通常用到的数学知识有二次函数、均值不等式以及三角函数等．但一定要依据物理理论对解的合理性及物理意义进行讨论或说明．(3)图解法：根据物体的平衡条件作出力的矢量图，如物体只受三个力，则这三个力构成封闭矢量三角形，然后根据图进行动态分析，确定最大值和最小值．此法简便、直观．例5　如图所示，物体A的质量M＝1 kg，静止在光滑水平面上的平板车B的质量m＝0.5 kg、长L＝1 m．某时刻A以v0＝4 m/s水平向右的初速度滑上平板车B的上表面，在A滑上B的同时，给B施加一个水平向右的拉力．忽略物体A的大小，已知A与B之间的动摩擦因数μ＝0.2，g取10 m/s2.试求：如果要使A不至于从B上滑落，拉力F应满足的条件．解析：物体A滑上平板车B以后，做匀减速运动，由牛顿第二定律，得μMg＝MaA，解得aA＝μg＝2 m/s2.物体A不从B的右端滑落的临界条件是A到达B的右端时，A、B具有共同的速度v1，联立解得v1＝3 m/s，aB＝6 m/s2，拉力F＝maB－μMg＝1 N.若Fμg，则上层管道一定会相对下层管道发生滑动【答案】C　 (　　)A．1.5H　　　　 B．2HC．2.75H　 D．3.25H【答案】C　4．[科学推理]如图所示，平台质量M＝70 kg，人的质量为m，滑轮及细绳质量不计，站在平台上的人竖直向下拉绳子使人和平台一起以a＝2 m/s2的加速度向上做匀加速运动，不计滑轮与轴之间的摩擦，g取10 m/s2，则下列说法正确的是 (　　)A．人对平台的压力小于自身重力，故人处于失重状态B．OA段绳中的拉力等于平台与人的总重力C．若人的质量m＝60 kg，则人对平台的压力大小为300 N【答案】D　5．[科学推理](多选)某缓冲装置的理想化模型如图所示，劲度系数足够大的轻质弹簧与轻杆相连，轻杆可在固定的槽内移动，与槽间的滑动摩擦力不变．轻杆向右移动不超过l时，装置可安全工作．一小车若以速度v0撞击弹簧，已知装置可安全工作，轻杆与槽间的最大静摩擦力等于滑动摩擦力f0，且不计小车与地面的摩擦．从小车与弹簧刚接触时开始计时到小车离开弹簧这段时间内，关于轻杆所受的摩擦力f随时间t变化的f－t图像可能正确的是 (　　)【答案】AC　【解析】如果小车撞击弹簧的速度较小，弹簧在压缩过程中轻杆一直保持静止，随着压缩量的增大，弹力增大，弹力和静摩擦力平衡，静摩擦力也随之增大；之后弹簧将小车弹开，压缩量减小，弹力减小，轻杆所受的静摩擦力减小，故A正确；当小车的撞击速度较大时，轻杆会与槽发生相对滑动．小车与弹簧刚接触时开始计时，根据胡克定律F＝kx，弹簧的弹力随压缩量的增大而增大，刚开始弹力小于最大静摩擦力，轻杆不动，处于平衡状态，根据受力平衡得f＝F＝kx，静摩擦力随弹力的增大而增大，当弹力等于最大静摩擦力时，轻杆开始移动；轻杆移动过程中，摩擦力等于滑动摩擦力f0，大小不变，小车和轻杆做减速运动，最终速度减为零，轻杆最终处于平衡状态，弹簧逐渐恢复原长，最后小车离开弹簧，此过程中摩擦力等于弹力，逐渐减小，故C正确，B、D错误．6．[科学推理]将一质量为m的小球靠近墙面竖直向上抛出，图甲是向上运动的频闪照片，图乙是下降时的频闪照片，O是运动的最高点，上升和下降的闪光频率相同．取重力加速度为g，假设小球所受阻力大小不变，则可估算小球受到的阻力大小约为 (　　)【答案】B　7．[科学推理](多选)一辆小车静止在水平地面上，bc是固定在车上的一根水平杆，物块A穿在杆上，通过细线悬吊着小物体B，B在小车的水平底板上，小车未动时细线恰好在竖直方向上．现使小车分四次分别以加速度a1、a2、a3 、a4向右匀加速运动，如图所示，四种情况下A、B均与车保持相对静止，且甲和乙中细线仍处于竖直方向．已知a1∶a2∶a3∶a4＝1∶2∶4∶8，A受到的摩擦力大小依次为f1、f2、f3、f4，则下列判断正确的是 (　　)A．f1∶f2＝1∶2　 B．f1∶f2＝2∶3C．f3∶f4＝1∶2 　 D．tan α＝2tan θ【答案】ACD　【解析】设A、B的质量分别为M、m，则由题图知，甲和乙中A在水平方向只受摩擦力作用，根据牛顿第二定律f1＝Ma1，f2＝Ma2，所以f1∶f2＝1∶2，故A正确，B错误；丙和丁中，以A、B整体为研究对象，受力分析如图所示，则f3＝(M＋m)a3，f4＝(M＋m)a4，可得f3∶f4＝1∶2，所以C正确；以B为研究对象，根据牛顿第二定律，可得mgtan θ＝ma3，mgtan α＝ma4，联立可得tan α＝2tan θ，故D正确．8．[科学探究]为测量动车启动过程中加速度的大小，某同学设计并实施了如下两个方案．方案甲：观察发现铁轨旁相邻里程基座之间的距离为s，用手表记录车厢从第1个里程基座运动到第2个里程基座的时间为t1，车厢从第2个里程基座运动到第3个里程基座的时间为t2.方案乙：将细绳的一端系在行李架上，另一端悬挂一个钢球，测量钢球到悬点的距离l，动车加速时，测出钢球偏离原平衡位置的水平距离d.(1)用方案甲测得动车的加速度的表达式为a1＝________；用方案乙测得动车的加速度的表达式为a2＝__________________.(2)任选一个方案，简述该方案的误差主要来源：____________.(2)方案甲的误差主要来源是时间的测量；方案乙的误差主要来源是长度的测量．9．[模型建构、科学推理]很多餐厅为能服务更多的顾客，服务员需要用最短的时间将菜肴送至顾客处(设菜品送到顾客处速度恰好为零)．某次服务员用单手托托盘方式(如图所示)给12 m远处的顾客上菜，要求全程托盘水平．托盘和盘子之间的动摩擦因数μ1＝0.15，托盘和手之间的动摩擦因数μ2＝0.2，服务员上菜时的最大速度为3 m/s.假设服务员加速、减速过程中做匀变速直线运动，且可认为最大静摩擦力等于滑动摩擦力．g取10 m/s2.求：(1)服务员运动的最大加速度；(2)服务员上菜所用的最短时间．【答案】(1)1.5 m/s2　(2)6 s【解析】(1)设盘子的质量为m，托盘的质量为M，以最大加速度运动时，盘子、托盘、手保持相对静止，则对盘子，由牛顿第二定律，有f1＝ma1，盘子与托盘相对静止，则f1≤f1max＝μ1mg，解得a1≤μ1g＝1.5 m/s2.对盘子和托盘整体，由牛顿第二定律，有f2＝(M＋m)a2，手和托盘相对静止，则f2≤f2max＝μ2(M＋m)g，解得a2≤μ2g＝2 m/s2，则最大加速度amax＝1.5 m/s2.减速运动时间t2＝t1＝2 s，位移x2＝x1＝3 m，匀速运动位移x3＝L－x1－x2＝6 m，上菜所用最短时间t＝t1＋t2＋t3＝6 s.