人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直教案

第八章 立体几何初步

8.6 空间直线、平面的垂直

8.6.1 直线与直线垂直

教学设计

一、教学目标

1.   掌握异面直线所成角的定义，会求两异面直线所成的角。
2.   掌握直线与直线垂直的定义。

二、教学重难点

1.   教学重点

异面直线所成角的定义，直线与直线垂直的定义。

2.   教学难点

求异面直线所成的角。

三、教学过程

1. 新课导入

与平行关系类似，垂直也是空间直线、平面之间的一种特殊位置关系，它在研究空间图形问题中具有重要的作用.类比平行关系的研究过程，本节将研究空间直线、平面之间的垂直关系，重点研究这些垂直关系的判定和性质。

2. 探索新知

空间两条直线的位置关系有三种：平行直线、相交直线和异面直线。在初中我们已经研究了平行直线和相交直线。本节我们主要研究异面直线，首先研究如何刻画两条异面直线的位置关系。

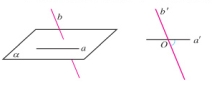我们知道，平面内两条直线相交形成4个角，其中不大于90°的角称为这两条直线所成的角（或夹角），它刻画了一条直线相对于另一条直线倾斜的程度.类似地，我们也可以用“异面直线所成的角”来刻画两条异面直线的位置关系。

如图，已知两条异面直线a，b，经过空间任一点O分别作直线，我们把直线与所成的角叫做异面直线a与b所成的角（或夹角）。

如果两条异面直线所成的角是直角，那么我们就说这两条异面直线互相垂直。直线a与直线b垂直，记作。

当两条直线a，b相互平行时，我们规定它们所成的角为0。所以空间两条直线所成角α的取值范围是0<a<90。

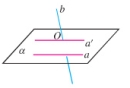学习课本P147-148例题1，2。从例1与例2的解答可以看到，为了简便，求异面直线a，b所成的角时，点O常取在两条异面直线中的一条上。例如取在直线b上，然后经过点O作直线，那么与所成的角就是异面直线a与b所成的角。

3. 课堂练习

1．若空间两条直线a和b没有公共点，则a与b的位置关系是(　　)

A．共面  B．平行　　C．异面　　D．平行或异面

答案：D　[若直线a和b共面，则由题意可知a∥b；若a和b不共面，则由题意可知a与b是异面直线．]

2．若OA∥O′A′，OB∥O′B′，且∠AOB＝130°，则∠A′O′B′为(　　)

A．130° B．50°

C．130°或50° D．不能确定

答案：C　[根据定理，∠A′O′B′与∠AOB相等或互补，即∠A′O′B′＝130°或∠A′O′B′＝50°.]

3．如图，在长方体ABCD­A1B1C1D1中，判断下列直线的位置关系：

(1)直线A1B与直线D1C的位置关系是________；

(2)直线A1B与直线B1C的位置关系是________；

(3)直线D1D与直线D1C的位置关系是________；

(4)直线AB与直线B1C的位置关系是________．

答案：(1)平行　(2)异面　(3)相交　(4)异面　[(1)在长方体ABCD­A1B1C1D1中，A1D1∥BC，A1D1＝BC，所以四边形A1BCD1为平行四边形，所以A1B∥D1C.

(2)直线A1B与直线B1C不同在任何一个平面内．

(3)直线D1D与直线D1C相交于点D1.

(4)直线AB与直线B1C不同在任何一个平面内．]

4．如图所示，空间四边形ABCD中，AB＝CD，AB⊥CD，E、F分别为BC、AD的中点，求EF和AB所成的角．

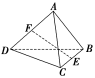
[解]　取AC的中点G，连接EG，FG，

则FG∥CD，EG∥AB，

所以∠FEG即为EF与AB所成的角，

且FG＝CD，EG＝AB，又AB＝CD，

所以FG＝EG.

又由AB⊥CD得FG⊥EG，所以∠FEG＝45°.

故EF和AB所成的角为45°.

4. 小结作业

小结：本节课学习了异面直线所成角的定义，直线与直线垂直的定义。

作业：完成本节课课后习题。

四、板书设计

8.6.1 直线与直线垂直

余弦定理、正弦定理应用举例

如图，已知两条异面直线a，b，经过空间任一点O分别作直线，我们把直线与所成的角叫做异面直线a与b所成的角（或夹角）。

如果两条异面直线所成的角是直角，那么我们就说这两条异面直线互相垂直。直线a与直线b垂直，记作。

当两条直线a，b相互平行时，我们规定它们所成的角为0。所以空间两条直线所成角α的取值范围是0<a<90。