高中数学人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.5 全称量词与存在量词表格教学设计
展开《全称量词与存在量词》教学设计
教学环节
教学内容
师生互动
设计意图
提出问题
引入新知
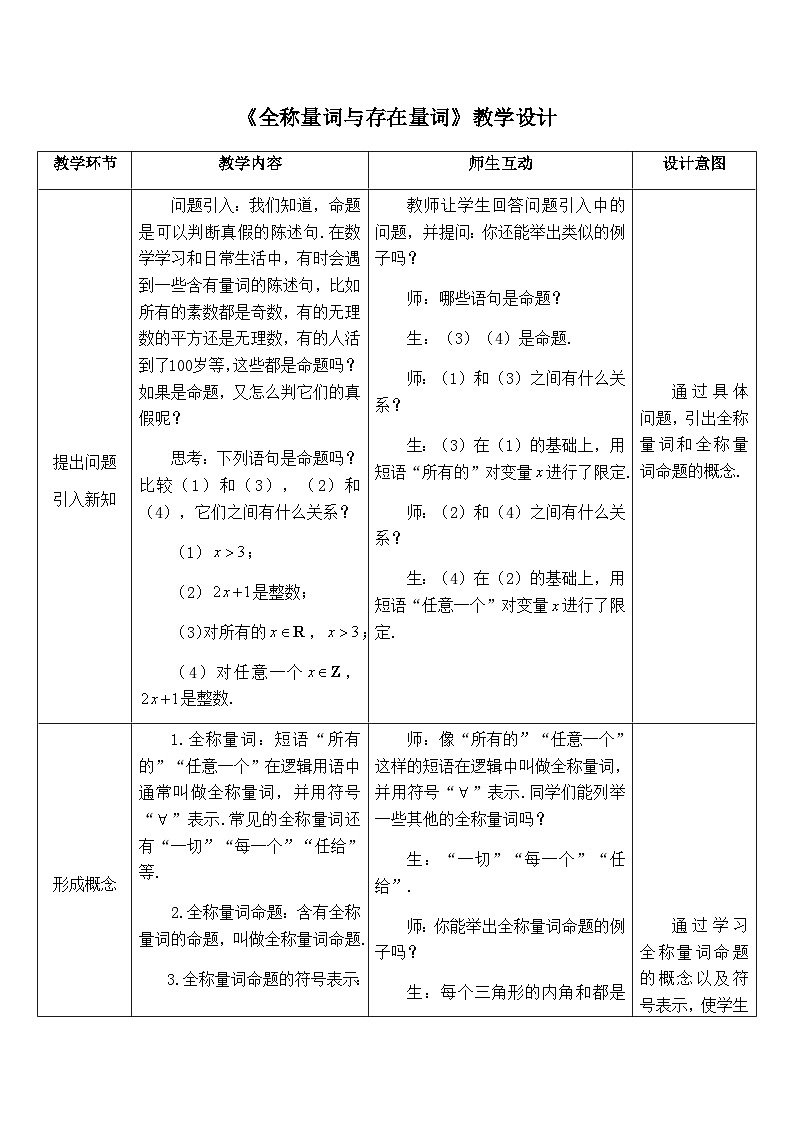
问题引入:我们知道,命题是可以判断真假的陈述句.在数学学习和日常生活中,有时会遇到一些含有量词的陈述句,比如所有的素数都是奇数,有的无理数的平方还是无理数,有的人活到了100岁等,这些都是命题吗?如果是命题,又怎么判它们的真假呢?
思考:下列语句是命题吗?比较(1)和(3),(2)和(4),它们之间有什么关系?
(1);
(2)是整数;
(3)对所有的,;
(4)对任意一个,是整数.
教师让学生回答问题引入中的问题,并提问:你还能举出类似的例子吗?
师:哪些语句是命题?
生:(3)(4)是命题.
师:(1)和(3)之间有什么关系?
生:(3)在(1)的基础上,用短语“所有的”对变量进行了限定.
师:(2)和(4)之间有什么关系?
生:(4)在(2)的基础上,用短语“任意一个”对变量进行了限定.
通过具体问题,引出全称量词和全称量词命题的概念.
形成概念
1.全称量词:短语“所有的”“任意一个”在逻辑用语中通常叫做全称量词,并用符号“”表示.常见的全称量词还有“一切”“每一个”“任给”等.
2.全称量词命题:含有全称量词的命题,叫做全称量词命题.
3.全称量词命题的符号表示:,.
师:像“所有的”“任意一个”这样的短语在逻辑中叫做全称量词,并用符号“”表示.同学们能列举一些其他的全称量词吗?
生:“一切”“每一个”“任给”.
师:你能举出全称量词命题的例子吗?
生:每个三角形的内角和都是.
师:很好!对给定的全称量词命题,如何判断它的真假呢?现在我们来看例1.
通过学习全称量词命题的概念以及符号表示,使学生在总结中提升数学抽象素养.
应用举例
例1(教材第25页例1)
补充1:如果一个大于1的整数,除1和自身外无其他正因数,则称这个正整数为素数.
补充2:判定全称量词命题真假的方法:集合中每个元素都满足,则“,”为真命题;如果在集合中能找到一个元素使不成立,
则“,”为假命题.
师:这3个全称量词命题的真假如何?
生:(1)(3)是假命题,(2)是真命题.
师;正确,怎么判断的呢?
生:通过举反例得到(1)(3)是假命题;通过能说明每一个都能满足,所以(2)是真命题.
师:你能总结判断全称量词命题真假的一般方法吗?
生:能.
通过具体实例,引导学生归纳出判断全称量词命题真假的方法,提升逻辑推理素养.
提出问题
引入新知
思考:下列语句是命题吗?比较(1)和(3),(2)和(4),它们之间有什么关系?
(1);
(2)能被2和3整除;
(3)存在一个,使;
(4)至少有一个,能被2和3整除.
师:哪些语句是命题?
生:(3)(4)是命题.
师:(1)和(3)之间有什么关系?
生:(3)在(1)的基础上,用短语“存在一个”对变量进行了限定.
师:(2)和(4)之间有什么关系?
生:(4)在(2)的基础上,用短语“至少有一个”对变量进行了限定.
通过具体问题,引出存在量词和存在量词命题的概念.
形成概念
1.存在量词:短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,并用符号“”表示.常见的存在量词还有“有些”“有一个”“对某些”“有的”等.
2.存在量词命题:含有存在量词的命题,叫做存在量词命题.
3.存在量词命题的符号表示:,.
师:像“存在一个”“至少有一个”等这些词称为存在量词,类比全称量词命题及其表示,你能得到什么结论?
生:存在量词命题及其符号表示.
师:你能举出存在量词命题的例子吗?
生:有一个素数不是奇数.
师:很好!对给定的存在量词命题,如何判断它的真假呢?现在我们来看例2.
通过类比,得出存在量词命题的概念以及符号表示,使学生在类比、总结中提升数学抽象素养.
应用举例
例2(教材第26页例2)
补充:判定存在量词命题真假的方法:如果在集合中能找到一个元素使成立,
则“,”为真命题;如果在集合中使成立的元素不存在,则“,”为假命题.
师:这3个存在量词命题的真假如何?
生:(1)(2)是假命题,(3)是真命题.
师:正确,怎么判断的呢?你的判断方法对其他具体的存在量词命题的判断有效吗?
学生讨论,回答问题.
通过例题,引导学生归纳出判断存在量词命题真假的方法,提升逻辑推理素养.
归纳总结
1.全称量词与存在量词.
2.全称量词命题与存在量词命题真假的判断方法.
学生回顾、总结,教师评价.
归纳总结本节课所学知识.
板书设计
1.5.1 全称量词与存在量词
一、新课
1.全称量词、全称量词命题
,
2.存在量词、存在量词命题
,
3.真假判断
(1)判断全称量词命题是真命题,需要验证中每个元素都满足;但要判断全称量词命题是假命题,只需举一个反例即可
(2)判断存在量词命题为真命题,只要在集合中能找到一个元素使成立即可,否则,这一存在量词命题就是假命题
二、例题
例1
例2
三、小结
1.全称量词与存在量词
2.全称量词命题与存在量词命题真假的判断方法
教学研讨
教学过程中,所用到的实例均含有全称量词或存在量词,未涉及从字面上看没有全称量词或存在量词,但却是全称量词命题或存在量词命题的实例,比如“线段的垂直平分线上的点到这条线段两个端点的距离相等”“负数的平方是正数”“三角形不都是中心对称图形”等,这些实例需不需要补充,在什么位置补充等问题可能需要根据学生的实际情况来决定.
高中人教A版 (2019)4.4 对数函数表格教案设计: 这是一份高中人教A版 (2019)4.4 对数函数表格教案设计,共4页。
人教A版 (2019)必修 第一册4.3 对数表格教案: 这是一份人教A版 (2019)必修 第一册4.3 对数表格教案,共5页。教案主要包含了问题导入,新课,例题,小结等内容,欢迎下载使用。
数学必修 第一册3.3 幂函数表格教案设计: 这是一份数学必修 第一册3.3 幂函数表格教案设计,共5页。教案主要包含了复习引入,新课探究,小结,作业等内容,欢迎下载使用。