数学必修 第一册3.3 幂函数表格教案设计
展开《幂函数》教学设计
教学环节
教学内容
师生互动
设计意图
复习引入
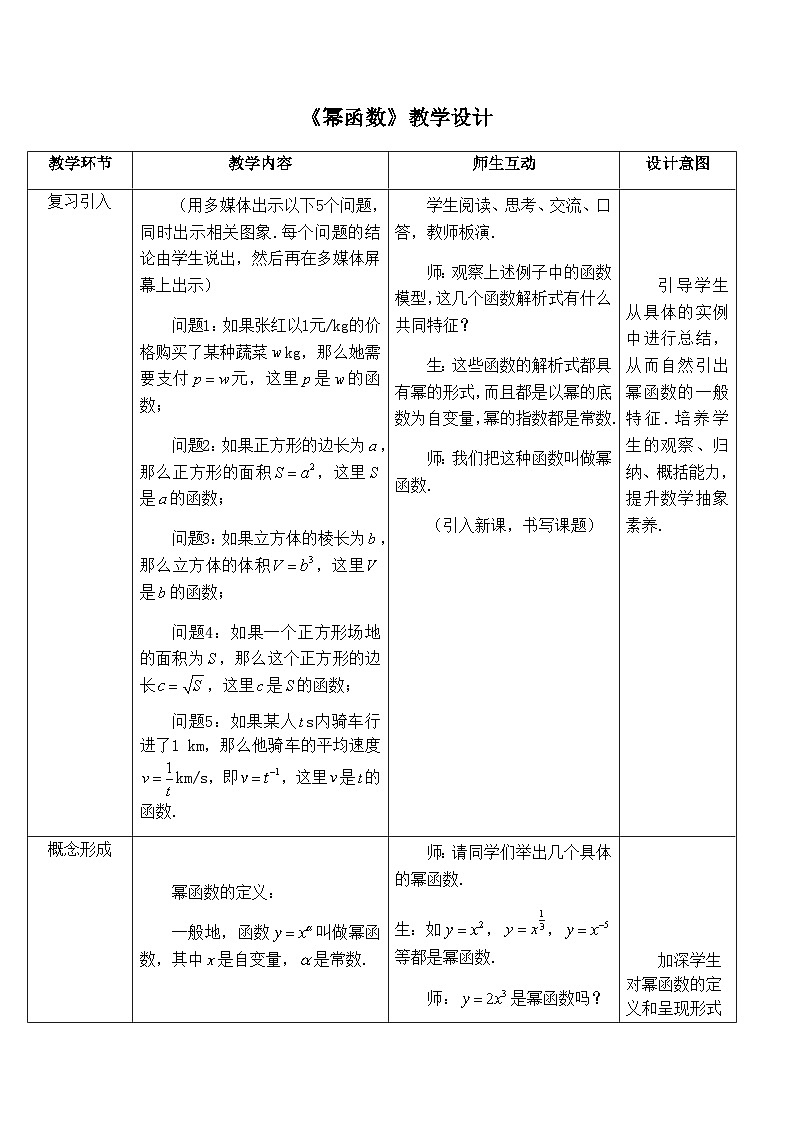
(用多媒体出示以下5个问题,同时出示相关图象.每个问题的结论由学生说出,然后再在多媒体屏幕上出示)
问题1:如果张红以1元/kg的价格购买了某种蔬菜kg,那么她需要支付元,这里是的函数;
问题2:如果正方形的边长为,那么正方形的面积,这里是的函数;
问题3:如果立方体的棱长为,那么立方体的体积,这里是的函数;
问题4:如果一个正方形场地的面积为,那么这个正方形的边长,这里是的函数;
问题5:如果某人s内骑车行进了1 km,那么他骑车的平均速度km/s,即,这里是的函数.
学生阅读、思考、交流、口答,教师板演.
师:观察上述例子中的函数模型,这几个函数解析式有什么共同特征?
生:这些函数的解析式都具有幂的形式,而且都是以幂的底数为自变量,幂的指数都是常数.
师:我们把这种函数叫做幂函数.
(引入新课,书写课题)
引导学生从具体的实例中进行总结,从而自然引出幂函数的一般特征.培养学生的观察、归纳、概括能力,提升数学抽象素养.
概念形成
幂函数的定义:
一般地,函数叫做幂函数,其中是自变量,是常数.
师:请同学们举出几个具体的幂函数.
生:如,,等都是幂函数.
师:是幂函数吗?
学生对比定义,得出否定答案.
加深学生对幂函数的定义和呈现形式的理解。
概念深化
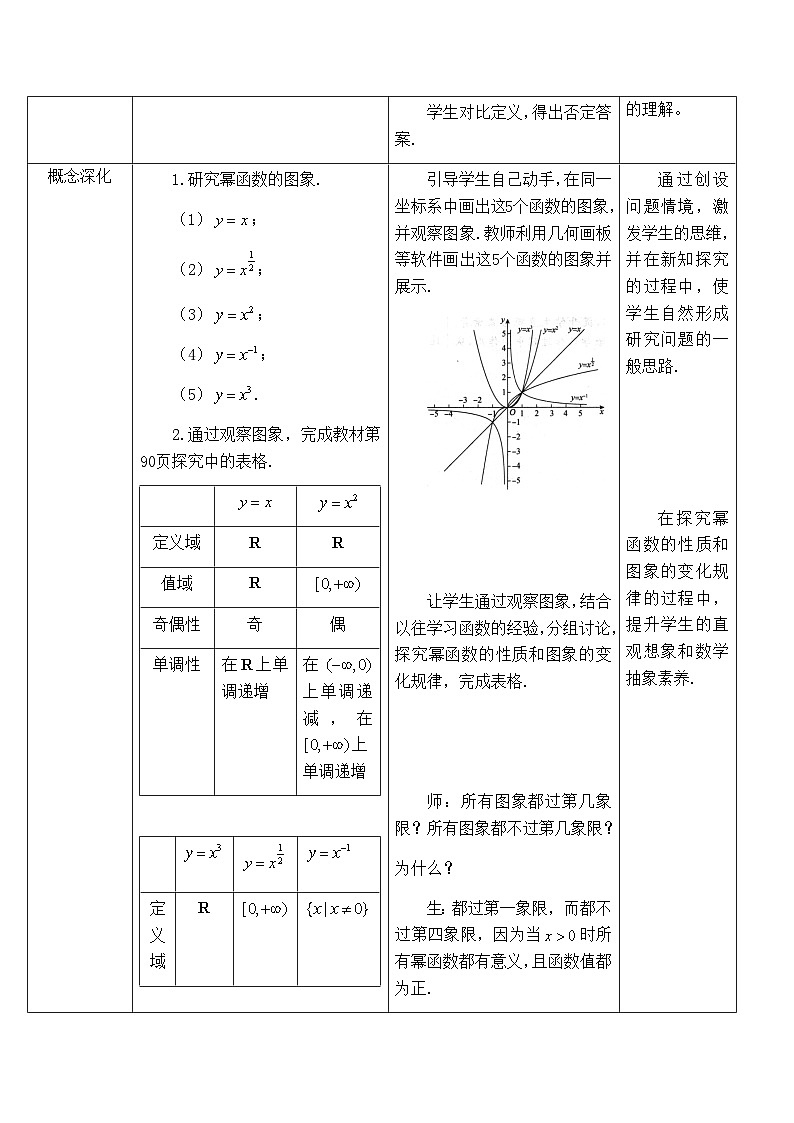
1.研究幂函数的图象.
(1);
(2);
(3);
(4);
(5).
2.通过观察图象,完成教材第90页探究中的表格.
定义域
值域
奇偶性
奇
偶
单调性
在上单调递增
在上单调递减,在上单调递增
定义域
值域
奇偶性
奇
非奇非偶
奇
单调性
在上单调递增
在上单调递增
在上单调递减,在上单调递减
3.幂函数的性质.
(1)所有的幂函数在都有定义,并且图象都过点.
(2)时,幂函数的图象都通过原点,并且在上是增函数(从左往右看,函数图象逐渐上升).
特别地,当时,,的图象都在图象的下方,形状向下凸.越大,下凸的程度越大.(你能找出原因吗?)
当时,,的图象都在的图象上方,形状向上凸,越小,上凸的程度越大.(你能说出原因吗?)
(3)时,幂函数的图象在区间
上是减函数.
在第一象限内,当向原点靠近时,图象在轴的右方无限逼近轴正半轴,当慢慢地变大时,图象在轴上方并无限逼近轴的正半轴.
引导学生自己动手,在同一坐标系中画出这5个函数的图象,并观察图象.教师利用几何画板等软件画出这5个函数的图象并展示.
让学生通过观察图象,结合以往学习函数的经验,分组讨论,探究幂函数的性质和图象的变化规律,完成表格.
师:所有图象都过第几象限?所有图象都不过第几象限?
为什么?
生:都过第一象限,而都不过第四象限,因为当时所有幂函数都有意义,且函数值都为正.
师:所有图象都过哪些点?
生:都过点.
师:什么样的幂函数的图象过原点,什么样的幂函数的图象不过原点?
生:幂的指数为正数时,函数图象过原点.幂的指数为负数时,函数图象不过原点.
师:图象在第一象限的位置关系是什么样的?
生:当时,指数小的图象在上方.当时,指数大的图象在上方.
通过创设问题情境,激发学生的思维,并在新知探究的过程中,使学生自然形成研究问题的一般思路.
在探究幂函数的性质和图象的变化规律的过程中,提升学生的直观想象和数学抽象素养.
应用举例
例 证明幂函数是增函数.
证明:函数的定义域是.
,,且,
则
.
因为,.
所以,
即幂函数在上是增函数.
小结:以上是用作差法证明函数的单调性,还可以用作商法证明函数的单调性.注意:在证得后,要比较与的大小,要注意分母的符号.
请同学们回顾一下如何证明一个函数是增函数,然后请一个学生作答.教师板书或投影答案.
教师强调教材中此例题的地位和作用:
(1)复习利用定义证明单调性的过程;
(2)幂函数的单调性很容易观察,强调严格判断的时候要用单调性进行证明;
(3)注意:幂函数的单调性很容易观察得出,所以在证明过程中直接用到了单调性,如直接判断.
增强学生对新知的应用能力,从而达到能力转型和对知识的理解.让学生在分析、证明的过程中提升逻辑推理素养.
归纳小结
1.幂函数的定义.
2.幂函数的图象.
3.幂函数的性质.
学生回顾反思,教师点评完善.
形成知识体系.
布置作业
教材第91页练习第1,2,3题.
学生独立完成.
巩固知识,提升能力.
板书设计
3.3 幂函数
一、复习引入
二、新课探究
1.幂函数的定义:一般地,函数叫做幂函数,其中是自变量,是常数
2.幂函数的图象
3.填表
幂函数的性质
4.例题
例 证明幂函数是增函数
三、小结
四、作业
教学研讨
本案例从具体的实例入手,通过观察、概括、总结共同特征,抽象出幂函数的概念,进而通过画图象、观察图象初步得到函数的性质.最后通过一道例题进行理论证明函数的单调性,既是复习,也是加深对幂函数的进一步认识.本案例的设计较好地提升了学生的直观想象、数学抽象和数学运算素养.
幂函数作为基本初等函数出现在高中数学中,地位和重要性不言而喻,是不是在案例中要强调幂函数的特征(比如系数为1,只有一项)?另外,案例设置了证明某个幂函数的单调性,对于利用幂函数的单调性去比较两数的大小的题型没有涉及,是不是也需要补充这方面的例题和练习呢?这些都值得思考.
人教A版 (2019)必修 第一册第三章 函数概念与性质3.3 幂函数优秀教案设计: 这是一份人教A版 (2019)必修 第一册第三章 函数概念与性质3.3 幂函数优秀教案设计,共6页。教案主要包含了目标和目标解析,教学问题诊断分析,教学支持条件,教学过程设计等内容,欢迎下载使用。
人教A版 (2019)必修 第一册4.3 对数表格教案: 这是一份人教A版 (2019)必修 第一册4.3 对数表格教案,共5页。教案主要包含了问题导入,新课,例题,小结等内容,欢迎下载使用。
人教A版 (2019)3.2 函数的基本性质表格教学设计: 这是一份人教A版 (2019)3.2 函数的基本性质表格教学设计,共5页。教案主要包含了复习,概念,例题,小结等内容,欢迎下载使用。