初中数学人教版八年级上册12.2 三角形全等的判定优秀教学设计及反思

这是一份初中数学人教版八年级上册12.2 三角形全等的判定优秀教学设计及反思，文件包含人教版初中数学八年级上册1221三角形全等的判定SSS课件pptx、人教版初中数学八年级上册1221三角形全等的判定SSS教案docx等2份教案配套教学资源，其中教案共8页， 欢迎下载使用。

人教版数学八年级上册
第十二章 全等三角形
12.2.1 三角形全等的判定(SSS)
1. 探究并掌握“边边边”判定三角形全等的方法；
2. 会用尺规作一个角等于已知角，了解图形的作法.
2．若两个三角形全等，则它们的三边对应______；反之，若两个三角形的三边对应相等，则这两个三角形_______．
1．在△ABC和△DEF中，若AB＝DE，BC＝EF，AC＝DF，则_____________________．
△ABC≌△DEF
全等
相等
3．下列命题正确的是( )A．有一边对应相等的两个等边三角形全等B．有两边对应相等的两个等腰三角形全等C．有一边对应相等的两个等腰三角形全等D．有一边对应相等的两个直角三角形全等
A
6
4．已知AB＝3，BC＝4，AC＝6，EF＝3，FG＝4，要使△ABC≌△EFG，则EG＝_______．
1. 全等三角形的定义
能够完全重合的两个三角形叫全等三角形.
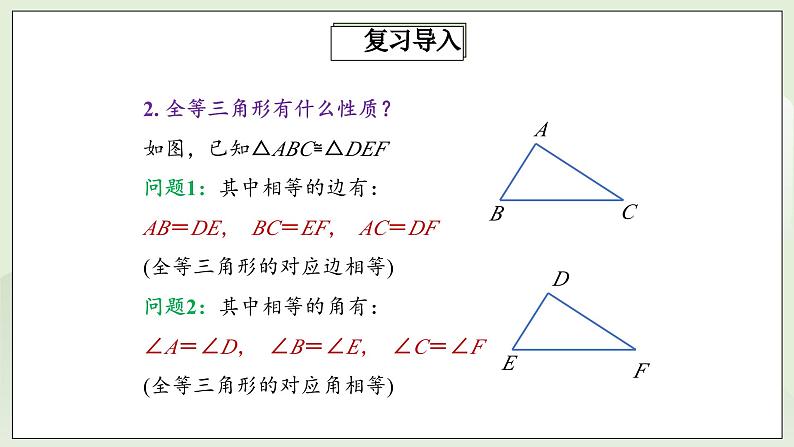
2. 全等三角形有什么性质？
问题1：其中相等的边有：
问题2：其中相等的角有：
∠A＝∠D， ∠B＝∠E， ∠C＝∠F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
AB＝DE， BC＝EF， AC＝DF
如图，已知△ABC≌△DEF
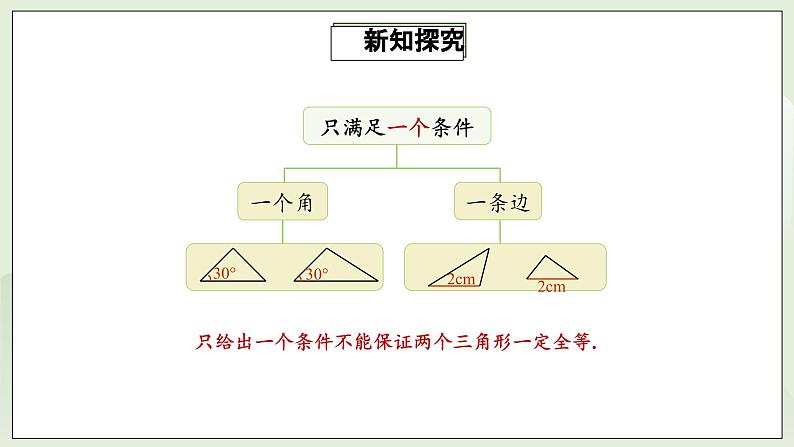
只满足一个条件
一个角
一条边
只给出一个条件不能保证两个三角形一定全等.
只满足两个条件
两条边
只给出两个条件也不能保证两个三角形一定全等.
满足三个条件
三个角
三条边
两角一边
两边一角
如果给出三个条件画三角形时，你能说出有哪几种可能的情况吗？
A ′
B′
C′
想一想：作图的结果反映了什么规律？你能用文字语言和符号语言概括吗？
(3)连接线段A'B'，A'C'.
画一个△A′B′C′ ，使A′B′＝AB ，B′C′ ＝BC，A′C′ ＝AC.
作法：
(1)画B′C′＝BC；
(2)分别以B'，C'为圆心，线段AB，AC长为半径画弧，两弧相交于点A'；
三边分别相等的两个三角形全等.(简写为“边边边”或“SSS”)
在△ABC和△DEF中，
∴ △ABC ≌△DEF(SSS).
几何语言表示：
例1 如图，有一个三角形钢架，AB ＝AC ，AD是连接点A与BC 中点D 的支架．求证：(1)△ABD ≌△ACD ．(2)∠BAD＝∠CAD.
例1 如图，有一个三角形钢架，AB ＝AC ，AD是连接点A与BC 中点D 的支架．求证：(1)△ABD ≌△ACD ．
证明：(1)∵D是BC中点，
∴BD＝DC．
在△ABD与△ACD中，
∴ △ABD ≌ △ACD ( SSS )．
例1 如图，有一个三角形钢架，AB ＝AC ，AD是连接点A与BC 中点D 的支架．求证：(2)∠BAD＝∠CAD.
证明：由(1)得△ABD≌△ACD，
∴ ∠BAD＝∠CAD.
(全等三角形对应角相等)
在△ABC 和△DCF中，
AB＝DC，
∴ △ABC ≌ △DCF
(已知)
(已证)
AC＝DF，
BC＝CF，
证明：∵C是BF中点，
∴BC＝CF.
(已知)
(SSS).
已知：如图，点B、E、C、F在同一直线上，AB＝DE，AC＝DF，BE＝CF.求证：(1)△ABC≌△DEF；(2)∠A＝∠D.
E
已知：如图，点B、E、C、F在同一直线上，AB＝DE，AC＝DF，BE＝CF. 求证：(1)△ABC≌△DEF；(2)∠A＝∠D.
E
证明：
∴△ABC≌△DEF ( SSS ).
在△ABC和△DEF中，
AB＝DE，AC＝DF，BC＝EF，
(已知)
(已知)(已证)
∵ BE＝CF，
∴ BC＝EF.
∴ BE+EC ＝ CF+CE，
(1)
(2)∵ △ABC≌ △DEF(已证)， ∴ ∠A＝∠D(全等三角形对应角相等).
证明：∵D是BC的中点，
∴BD＝CD.
在△ABD与△ACD中，
AB＝AC(已知)，
BD＝CD(已证)，
AD＝AD(公共边)，
∴△ABD≌△ACD(SSS)，
∴∠B＝∠C.
已知：∠AOB．求作：∠A′O′B′，使∠A′O′B′＝∠AOB．
例3 用尺规作一个角等于已知角．
O
D
B
C
A
O′
C′
A′
B′
D ′
作法：
(1)以点O为圆心，任意长为半径画弧，分别交OA，OB 于点C、D；
(2)画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；
(3)以点C′为圆心，CD长为半径画弧，与第2 步中所画的弧交于点D′；
(4)过点D′画射线O′B′，则∠A′O′B′＝∠AOB．
1.下列结论错误的是(　 )A．全等三角形对应角所对的边是对应边B．全等三角形两条对应边所夹的角是对应角C．全等三角形是一种特殊三角形D．如果两个三角形都与另一个三角形全等，那么这两个三角形也全等
C
2.如图，AB＝CD，AD＝BC， 则下列结论： ①△ABC≌△CDB； ②△ABC≌△CDA；③△ABD ≌△CDB； ④BA∥DC. 正确的个数是 ( )A . 1个 B. 2个 C. 3个 D. 4个
C
3．如图，在△ABC中，∠BAC＝60°，将△ABC绕着点A顺时针旋转40°后得到△ADE，则∠BAE的度数为__________．
100°
60°
40°
证明：(1)∵ AD＝FB，∴AB＝FD (等式性质).
AC＝FE(已知)，BC＝DE(已知)，AB＝FD(已证)，
(2)∵△ABC≌△FDE(已证).
∴ ∠C＝∠E(全等三角形的对应角相等).
在△ABC和△FDE中，
∴△ABC≌△FDE(SSS)；
即OC是∠AOB的平分线.
∴ ∠MOC＝∠NOC (全等三角形的对应角相等)
证明：在 △OMC和△ONC中，
5. 工人师傅常用角尺平分一个任意角， 做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与M、N重合，过角尺顶点C的射线OC便是∠AOB的平分线. 为什么？
∴ △OMC≌ △ONC (SSS).
　　　　　
(边边边或SSS)
课程结束
版权声明
人教统编版高中语文选择性必修上册
教习网//www.enxinlong.com/（以下简称“本网站”）系属深圳市智学帮科技有限公司（以下简称“本公司”）旗下网站，为维护本公司合法权益，现依据相关法律法规作出如下郑重声明：1.本文件仅用于个人学习、研究，不得用于商业性或盈利性用途，不得侵犯本司及相关权利人的合法权利。一旦发现侵权，本公司将联合司法机关获取相关用户信息并要求侵权者承担相关法律责任。2.本网站上所有原创内容，是本公司依据相关法律法规，安排专项经费运营规划，组织老师创作完成，著作权归属本公司所有。3.经由网站用户上传至本网站的课件、教案、学案、试卷等内容，其作品仅代表作者本人观点，本网站不保证其内容的有效性，凡因本作品引发的任何法律纠纷，均由上传用户承担法律责任，本网站仅有义务协助司法机关了解事实情况。
兼职招募
人教统编版高中语文选择性必修上册
教习网（www.enxinlong.com）专为 K12教育老师提供同步备课资料下载、教学经验学习等服务的互联网教育平台。为了进一步完善网站的资料体系，最大化满足用户的精品资源需求，现诚邀全国各地优秀一线老师加入教习网兼职创作老师团队，参与资源建设，获取高额现金收益。兼职招募详情请看：//www.enxinlong.com/article-5396.html
公益助学
人教统编版高中语文选择性必修上册
教习网诚挚地为各位老师推荐两款免费的朗读小程序，可用于课前预习、课中学习和课后复习，打开微信扫下方二维码即可使用，欢迎分享广大师生使用。
福利社群
人教统编版高中语文选择性必修上册
查看下方网页链接，扫码添加客服加入教习网专属福利社群： 更多福利，等您来领取：//www.enxinlong.com/act/event/pc/fuli.html