人教版初中数学八年级上册13.5第6讲《垂直平分线与将军饮马模型》专项突破 课件PPT(送教案)

13.5第6讲《垂直平分线与将军饮马模型》专项突破  预习案

测试题1  关于线段的垂直平分线有以下说法：

①一条线段的垂直平分线的垂足，也是这条线段的中点;

②线段的垂直平分线是一条直线;

③一条线段的垂直平分线是这条线段的唯一对称轴.

其中，正确的说法有（　　）

A. 1个       B. 2个       C. 3个       D. 0个

答案：B

测试题2  如图，AC=AD，BC=BD，则有（　　）

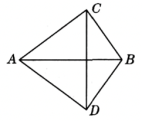
A. AB垂直平分CD                  B. CD垂直平分AB

C. AB与CD互相垂直平分           D. 以上都不正确

答案：A

测试题3  如图，∠BAC=130°，若MP和QN分别垂直平分AB和AC，则∠PAQ等于（    ）

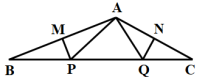
A. 50°        B. 75°         C. 80°          D. 105°

答案：C

解析过程：∵MP和QN分别垂直平分AB和AC，

∴BP=AP，CQ=AQ，

∴∠B=∠PAB，∠C=∠QAC，

∵∠BAC=130°，

∴∠B+∠C=180°﹣∠BAC=50°，

∴∠BAP+∠CAQ=50°，

∴∠PAQ=∠BAC﹣（∠PAB+∠QAC）=130°﹣50°=80°，

故选：C．

测试题4  如图，在△ABC中，AB=AC，DE垂直平分AB，分别交AB、AC于点D、E，若∠EBC=30°，则∠A=（    ）

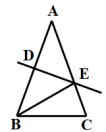
A. 30°         B. 35°         C. 40°          D. 45°

答案：C

解析过程：设∠A为x，

∵DE垂直平分AB，

∴EA=EB，

∴∠EBA=∠A=x，

∴∠BEC=2x，

∵AB=AC，

∴∠ABC=∠C，

∴30°+x+30°+2x=180°，

解得，x=40°，

故选：C．

测试题5  如图所示,一牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC＝BD.若A到河岸CD的中点距离为500米,则牧童从A处把牛牵到河边饮水后再回家,所走的路程最短是(    )

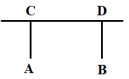
A. 500米            B. 600米

C. 800米               D. 1000米

答案：D

解析过程：如图所示,作点A关于直线CD的对称点A1.②连接A1B交CD于M,

则在M处饮水所走的路程最短.

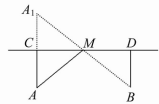
根据对称得:A1C＝AC＝BD,∠A1CM＝∠BDM,∠A1MC＝∠BMD,故△A1CM≌△BDM.

所以A1M＝BM,CM＝DM,所以M为CD的中点,AM＝500 米,

所以A1B＝2×500＝1000(米).故最短路程为1000米.