数学八年级上册14.1.1 同底数幂的乘法优秀教案
展开八年级上册14.1.1同底数幂的乘法 教案
学习目标:
1.回顾学过有关知识。并写出来;
2、理解并掌握同底数幂的乘法法则;
3、能够运用同底数幂的乘法法则进行相关计算;
4、通过对同底数幂的乘法运算法则的推导与总结,提升自身的推理能力。
学习重难点:
重难点:同底数幂乘法的运算性质、同底数幂乘法的运算性质的灵活运用。
一、合作探究
探究点1:同底数幂的乘法法则
 算一算:
算一算:
根据乘法的运算律,计算下列各题:
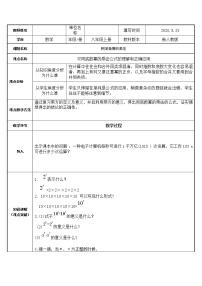
(1)a2 ·a6 ·a3=(a2 · ______)·______=a ________ ;
(2)x ·x2 ·x3=(x · ______)·______=x ________ .
比一比:
![]() am · an =_________ am · an · ap =_________.
am · an =_________ am · an · ap =_________.
想一想:
如果将am 中a的换成(x+y),等式是否仍然成立?请说明理由.
(x+y)m ·(x+y)n _________ (x+y)m+n(填“=”或“≠”)
理由是:
要点归纳:公式am · an = am+n中的底数a不仅可以代表数、单项式,还可以代表多项式等其他代数式.
典例精析
例1 计算
(1)x2 · x5 ; (2)a · a6; (3)(-2) × (-2)4 × (-2)3; (4) xm · x3m+1.
例2计算:
(1)(a+b)4 · (a+b)7 ; (2)(m-n)3 ·(m-n)5 ·(m-n)7 ; (3)(x-y)2·(y-x)5.
探究点2:同底数幂乘法法则的逆用
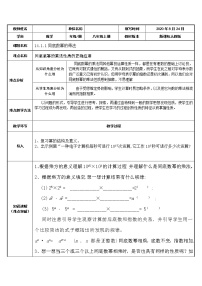
想一想:am+n可以写成那两个因式的积?
填一填:若xm =3 ,xn =2,那么,
(1)xm+n =_____×_____=_____×_____ =_____;
(2)x2m =_____×_____=_____×_____ =_____;
(3)x2m+n =_____×_____=_____×_____ =_____.
典例精析
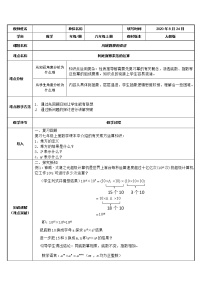
例3:(1)若xa=3,xb=4,xc=5,求2xa+b+c的值;
(2)已知23x+2=32,求x的值.
二、课堂小结
同底数幂的乘法法则:am · an =_________ (m、n都是正整数).即同底数幂相乘, 底数______,指数______.
我的收获
__________________________________________________________________________________________________________________________________________________________
初中数学人教版八年级上册14.1.1 同底数幂的乘法优秀教学设计: 这是一份初中数学人教版八年级上册14.1.1 同底数幂的乘法优秀教学设计,共5页。教案主要包含了创设情境,导入新课,探究问题,获取新知,巩固练习,加深所学,归纳小结,深化新知,当堂测试,检验所学等内容,欢迎下载使用。
人教版八年级上册14.1.1 同底数幂的乘法教案: 这是一份人教版八年级上册14.1.1 同底数幂的乘法教案,共7页。教案主要包含了回顾复习,应用新知,体验成功,作业布置,板书,教学反思等内容,欢迎下载使用。
人教版八年级上册14.1.1 同底数幂的乘法教学设计: 这是一份人教版八年级上册14.1.1 同底数幂的乘法教学设计,共2页。教案主要包含了创设情境,提出问题,形成法则,应用新知,体验成功,变式训练,激发情智,小结等内容,欢迎下载使用。