人教版初中数学八年级上册14.4.3 第9讲《因式分解》基础巩固 课件PPT(送教案)

这是一份人教版初中数学八年级上册14.4.3 第9讲《因式分解》基础巩固 课件PPT(送教案)，文件包含人教版初中数学八年级上册1443第9讲《因式分解》基础巩固课件pptx、人教版初中数学八年级上册1443第9讲《因式分解》基础巩固教案docx等2份教案配套教学资源，其中教案共6页， 欢迎下载使用。
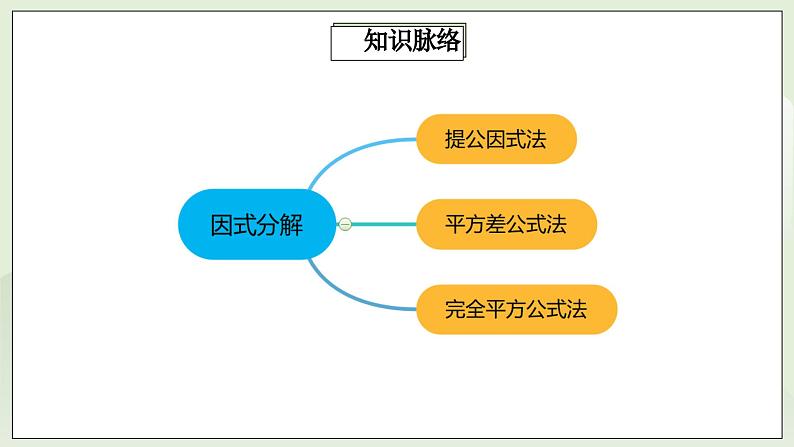
14.4.3第9讲《因式分解》基础巩固  教案一、知识目标重点： 掌握提公因式法、公式法进行因式分解的方法. 难点： 能在复杂的多项式中发现能用公式因式分解的模型.二、考情分析考查题型：单选、填空、解答题 考查分值：10-15分左右三、课堂教学思维与流程知识点1  提公因式法提公因式法→例题与练习知识点2  平方差公式法平方差公式法→例题与练习知识点3  完全平方公式法完全平方公式法→例题与练习  知识点1 提公因式法1.公因式：多项式中各项都含有的公共因式叫这个多项式的公因式．注意：①公因式可以是单项式，也可以是多项式，还可以是多项式幂的形式；②当多项式的第一项系数是负数时，公因式的符号应取“－”；③取多项式各项系数的最大公约数为公因式的系数；④把多项式各项都含有的相同字母（或因式）的最低次幂的积作为公因式的因式．2.提公因式法：一般地，如果多项式的各项有公因式，可以把这个公因式提取出来，将多项式写成公因式与另一个因式的乘积的形式，这种分解因式的方法叫做提公因式法．实质:逆用乘法分配律将多项式进行变形．知识提炼：提公因式法分解因式的依据是逆用乘法分配律，即：pa+pb+pc=p（a+b+c） 例题1 把下列各式因式分解：（1）6x3y－9x2y2z2；              （2）－2a3＋8a2－2a；（3）4m3n2－6m2n3＋12m2n2；    （4）3a（b－c）－6（b－c）【解析】（1）原式＝3x2y·2x－3x2y·3yz2＝3x2y（2x－3yz2）；（2）原式＝－（2a·a2－2a·4a＋2a·1）＝－2a（a2－4a＋1）；（3）原式＝2m2n2·2m－2m2n2·3n＋2m2n2·6＝2m2n2（2m－3n＋6）；（4）原式＝3（b－c）·a－3（b－c）·2＝3（b－c）（a－2）。技巧点拨：一找（找公因式）、二提（提公因式）.练习1-1 因式分解：（1）－3x3y2＋6x2y3＋3x2y2；（2）2mn（b－3a）2＋5m2（3a－b）2－7m（3a－b）2。【解析】（1）－3x3y2＋6x2y3＋3x2y2＝－3x2y2·x－3x2y2·（－2y）－3x2y2·（－1）＝－3x2y2（x－2y－1）；（2）2mn（b－3a）2＋5m2（3a－b）2－7m（3a－b）2＝2mn（3a－b）2＋5m2（3a－b）2－7m（3a－b）2＝m （3a－b）2（2n＋5m－7）。练习1-2 已知2a＋b＝6，a－3b＝－3，求14b（a－3b）2－4（3b－a）3的值。【解析】原式＝2（a－3b）2[7b＋2（a－3b）]＝2（a－3b）2（2a＋b），当2a＋b＝6，a－3b＝－3时，原式＝2×（－3）2×6＝2×9×6＝108技巧点拨：一找（找公因式）、二提（提公因式）、三代入. 知识点2 平方差公式法两数的平方差，等于这两个数的和与这两个数的差的积．即a2－b2＝（a＋b）（a－b）．注意：（1）先提公因式，在观察能否运用平方差公式；（2）因式分解必须分解到多项式中的每一个因式都不能再分解为止.知识提炼：平方差公式法：a2－b2＝（a＋b）（a－b）a、b既可以是单项式，也可以是多项式例题2  分解因式：（1）x4－y4；（2）-2x6+32x2.【解析】（1）x4－y4＝（x2＋y2）（x2－y2）＝（x2＋y2）（x＋y）（x－y）．（2）原式。技巧点拨：1.套公式：a2-b2=（a+b）（a-b）；2.分解到不能再分解为止.练习2-1  因式分解：x2y4－x4y2＝            .【解析】原式＝x2y2（y2－x2）＝x2y2（y－x）（y＋x），故答案为：x2y2（y－x）（y＋x）练习2-2  因式分解：（1）9（m＋n）2－（m－n）2；（2）p4－16。【解析】 （1）9（m＋n）2－（m－n）2＝[3（m＋n）]2－（m－n）2＝[3（m＋n）＋（m－n）] [3（m＋n）－（m－n）]＝（3m＋3n＋m－n）（3m＋3n－m＋n）＝（4m＋2n）（2m＋4n）＝4（2m＋n）（m＋2n）。（2）p4－16＝（p2）2－42＝（p2＋4）（p2－4）＝（p2＋4）（p＋2）（p－2）。练习2-3  已知4m＋n＝40，2m－3n＝5．求（m＋2n）2－（3m－n）2的值．【解析】 （m＋2n）2－（3m－n）2＝（m＋2n＋3m－n）（m＋2n－3m＋n）＝（4m＋n）（3n－2m）＝－（4m＋n）（2m－3n），当4m＋n＝40，2m－3n＝5时，原式＝－40×5＝－200．练习2-4  若，则n=___________.【解析】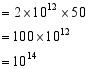∴n=14. 知识点3 完全平方公式法两个数的平方和加上（或减去）这两个数的积的2倍，等于这两个数的和（或差）的平方．即a2±2ab＋b2＝（a±b）2注意：（1）先提公因式，在观察能否运用完全平方公式；（2）因式分解必须分解到多项式中的每一个因式都不能再分解为止.知识提炼：完全平方公式法：a2±2ab＋b2＝（a±b）2a、b既可以是单项式，也可以是多项式.例题3  分解因式：（1）2a3－4a2b＋2ab2；（2）（a2＋b2）2－4a2b2．【解析】（1）2a3－4a2b＋2ab2＝2a（a2－2ab＋b2）＝2a（a－b）2；（2）原式＝（a2＋b2＋2ab）（a2＋b2－2ab）＝（a＋b）2（a－b）2．技巧点拨：1.套公式：a2±2ab＋b2＝（a±b）2；2.一提、二套、三分解.练习3-1 因式分解：（1）a2＋10a＋25；                  （2）m2－12mn＋36n2；（3）2mx2－4mx＋2m。【解析】（1）a2＋10a＋25＝a2＋2·a·5＋52＝（a＋5）2；                  （2）m2－12mn＋36n2＝m2－2·m·6n＋（6n）2＝ （m－6n）2； （3）2mx2－4mx＋2m＝2m（x2－2x＋1）＝2m（x－1）2。练习3-2 若m=2n+1，则m2-4mn+4n2的值是         .【解析】解析：∵，∴，又∵，∴原式＝。练习3-3  已知︱xy－4︱＋（x－2y－2）2＝0，求x2＋4xy＋4y2的值．【解析】∵︱xy－4︱＋（x－2y－2）2＝0，∴xy＝4，x－2y＝2，∵（x－2y）2＋8xy＝（x＋2y）2，∴22＋8×4＝（x＋2y）2，所以（x＋2y）2＝36．故x2＋4xy＋4y2＝（x＋2y）2＝36． 1. 提公因式法一找（找公因式）、二提（提公因式）.2. 平方差公式法（1）套公式：a2-b2=（a+b）（a-b）；（2）分解到不能再分解为止.3. 完全平方公式法（1）套公式：a2±2ab＋b2＝（a±b）2；（2）一提、二套、三分解.