高中数学（人教A版2019）选择性必修第三册 第七章 随机变量及其分布列 章末检测（含解析）

第七章随机变量及其分布列章末检测

一、单选题

1、袋中装有10个红球、5个黑球．每次随机抽取1个球后，若取得黑球则另换1个红球放回袋中，直到取到红球为止．若抽取的次数为ξ，则表示“放回5个红球”事件的是(　　)

A．ξ＝4　　　B．ξ＝5　　　C．ξ＝6　　　D．ξ≤5

2、设A，B为两个事件，且P(A)＞0，若P(AB)＝，P(A)＝，则P(B|A)＝(　　)

A.   B.      C.     D.

3、若随机变量X～B，则P(X＝3)等于(　　)

A.   B.    C.     D.

4、某物理量的测量结果服从正态分布N(10，σ2)，下列结论中不正确的是(　　)

A．σ越小，该物理量在一次测量中在(9.9,10.1)的概率越大

B．σ越小，该物理量在一次测量中大于10的概率为0.5

C．σ越小，该物理量在一次测量中小于9.99与大于10.01的概率相等

D．σ越小，该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等

5、离散型随机变量X的概率分布规律为P(X＝n)＝(n＝1，2，3，4)，其中a是常数，则P的值为(　　)

A.   B.    C.     D.

6、已知随机变量的分布列如下，且E(ξ)＝6.3，则a的值为(　　)

A.5   B.6    C.7     D.8

7、含有海藻碘浓缩液的海藻碘盐，是新一代的碘盐产品．海藻中的碘80%为无机碘，10%～20%为有机碘，海藻碘盐兼备无机碘和有机碘的优点．某超市销售的袋装海藻碘食用盐的质量X(单位：克)服从正态分布N(400,4)，某顾客购买了4袋海藻碘食用盐，则至少有2袋的质量超过400克的概率为(　　)

A． B．

C． D．

8、盒中有a个红球，b个黑球，随机地从中抽取一个，观察其颜色后放回，并加上其同色球c个，再从盒中抽取一球，则第二次抽出的是黑球的概率是(　　)

A.　　　　　　　　 B.

C.   D.

二、多选题

9、设离散型随机变量X的分布列为

若离散型随机变量Y满足Y＝2X＋1，则下列结果正确的有(　　)

A.q＝0.1 

B.E(X)＝2，D(X)＝1.4

C.E(X)＝2，D(X)＝1.8 

D.E(Y)＝5，D(Y)＝7.2

10、已知随机变量X服从正态分布N(100，102)，则下列选项正确的是(　　)

(参考数值：随机变量ξ服从正态分布N(μ，σ2)，则P(μ－σ≤ξ≤μ＋σ)≈0.682 7，P(μ－2σ≤ξ≤μ＋2σ)≈0.954 5，P(μ－3σ≤ξ≤μ＋3σ)≈0.997 3)

A.E(X)＝100 

B.D(X)＝100

C.P(X＞90)≈0.841 35 

D.P(X＜120)≈0.998 65

11、某人参加一次测试，在备选的10道题中，他能答对其中的5道.现从备选的10道题中随机抽出3道题进行测试，规定至少答对2题才算合格.则下列选项正确的是(　　)

A.答对0题和答对3题的概率相同，都为

B.答对1题的概率为

C.答对2题的概率为

D.合格的概率为

12、甲罐中有3个红球、2个黑球，乙罐中有2个红球、2个黑球，先从甲罐中随机取出一球放入乙罐，以A表示事件“从甲罐取出的球是红球”，再从乙罐中随机取出一球，以B表示事件“从乙罐取出的球是红球”，则(　　)

A．P(A)＝   B．P(B|A)＝

C．P(B)＝   D．P(A|B)＝

三、填空题

13、已知随机变量X的分布规律为P(X＝i)＝(i＝1，2，3)，则P(X＝2)＝________．

14、某学校有100人参加暑期社会实践，实践结束时的综合能力测试成绩X近似服从正态分布N(110，σ2)，若P(100≤X≤110)＝0.35，则综合能力测试成绩在120分以上的人数大约为_______．

15、近年来，新能源汽车技术不断推陈出新，新产品不断涌现，在汽车市场上影响力不断增大．动力蓄电池技术作为新能源汽车的核心技术，它的不断成熟也是推动新能源汽车发展的主要动力．假定现在市售的某款新能源汽车上，车载动力蓄电池充放电循环次数达到2 000次的概率为85%，充放电循环次数达到2 500次的概率为35%.若某用户的自用新能源汽车已经经过了2 000次充电，那么他的车能够充电2 500次的概率为________．

16、在一次随机试验中，事件A发生的概率为p，事件A发生的次数为ξ，则数学期望Eξ＝________，方差Dξ的最大值为________．

四、解答题

17、有编号为1，2，3，…，n的n个学生，入座编号为1，2，3，…，n的n个座位，每个学生规定坐一个座位，设学生所坐的座位号与该生的编号不同的学生人数为X，已知X＝2时，共有6种坐法.

(1)求n的值；

(2)求随机变量X的分布列.

18、现有6个节目准备参加比赛，其中4个舞蹈节目，2个语言类节目，如果不放回地依次抽取2个节目，求

(1)第1次抽到舞蹈节目的概率；

(2)第1次和第2次都抽到舞蹈节目的概率；

(3)在第1次抽到舞蹈节目的条件下，第2次抽到舞蹈节目的概率.

19、甲、乙两人玩投篮游戏，规则如下：两人轮流投篮，每人至多投2次，甲先投，若有人投中即停止投篮，结束游戏，已知甲每次投中的概率为，乙每次投中的概率为，求：

(1)乙投篮次数不超过1的概率；

(2)记甲、乙两人投篮次数总和为ξ，求ξ的分布列和期望.

20、某高校通过自主招生方式在贵阳招收一名优秀的高三毕业生，经过层层筛选，甲、乙两名学生进入最后测试，该校设计了一个测试方案：甲、乙两名学生各自从6个问题中随机抽3个问题.已知这6个问题中，学生甲能回答正确其中的4个问题，而学生乙能回答正确每个问题的概率均为，甲、乙两名学生对每个问题的回答都是相互独立、互不影响的.

(1)求甲、乙两名学生共答对2个问题的概率；

(2)请从期望和方差的角度分析，甲、乙两名学生哪位被录取的可能性更大.

21、为了拓展网络市场，某公司为手机客户端用户推出了多款APP应用，如“农场”“音乐”“读书”等.市场调查表明，手机用户在选择以上三种应用时，选择“农场”、“音乐”、“读书”的概率分别为，，.现有甲、乙、丙三位手机客户端用户独立任意选择以上三种应用中的一种进行安装.

(1)求三人所选择应用互不相同的概率；

(2)记ξ为三人中选择的应用是“农场”与“音乐”的人数，求ξ的分布列和期望.

22、十九大以来，某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求，带领广大农村地区人民群众脱贫奔小康．经过不懈的奋力拼搏，新农村建设取得巨大进步，农民年收入也逐年增加，为了制定提升农民收入、实现2020年脱贫的工作计划，该地扶贫办统计了2019年50位农民的年收入并制成如下频率分布直方图：

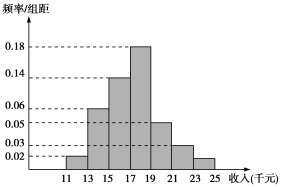
(ⅰ)根据频率分布直方图，估计50位农民的平均年收入(单位：千元)；(同一组数据用该组数据区间的中点值表示)；

(ⅱ)由频率分布直方图，可以认为该贫困地区农民年收入X服从正态分布N(μ，σ2)，其中μ近似为年平均收入，σ2近似为样本方差s2，经计算得s2＝6.92，利用该正态分布，求：

①在扶贫攻坚工作中，若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准，则最低年收入标准大约为多少千元？

②为了调研“精准扶贫，不落一人”的政策要求落实情况，扶贫办随机走访了1 000位农民．若每位农民的年收入互相独立，问：这1 000位农民中的年收入不少于12.14千元的人数最有可能是多少？

附参考数据：≈2.63，若随机变量X服从正态分布N(μ，σ2)，则P(μ－σ≤X≤μ＋σ)＝0.682 7，P(μ－2σ≤X≤μ＋2σ)＝0.954 5，P(μ－3σ≤X≤μ＋3σ)＝0.997 3.