高考数学全国甲卷（文）3年（2021-2023）真题分类汇编-填空题

这是一份高考数学全国甲卷（文）3年（2021-2023）真题分类汇编-填空题，共9页。试卷主要包含了填空题等内容，欢迎下载使用。
高考数学全国甲卷（文）3年（2021-2023）真题分类汇编-填空题

一、填空题
1．（2023年高考全国甲卷数学（文）真题）记为等比数列的前项和．若，则的公比为 ．
2．（测试使用，请勿下载（全国甲卷理数））若为偶函数，则 ．
3．（测试使用，请勿下载（全国甲卷理数））若x，y满足约束条件，设的最大值为 ．
4．（2023年高考全国甲卷数学（文）真题）在正方体中，为的中点，若该正方体的棱与球的球面有公共点，则球的半径的取值范围是 ．
5．（2022年全国高考甲卷数学（文）试题）已知向量．若，则 ．
6．（2022年全国高考甲卷数学（文）试题）设点M在直线上，点和均在上，则的方程为 ．
7．（2022年全国高考甲卷数学（文）试题）记双曲线的离心率为e，写出满足条件“直线与C无公共点”的e的一个值 ．
8．（2022年全国高考甲卷数学（理）试题）已知中，点D在边BC上，．当取得最小值时， ．
9．（2021年全国高考甲卷数学（文）试题）若向量满足，则 .
10．（2021年全国高考甲卷数学（文）试题）已知一个圆锥的底面半径为6，其体积为则该圆锥的侧面积为 .
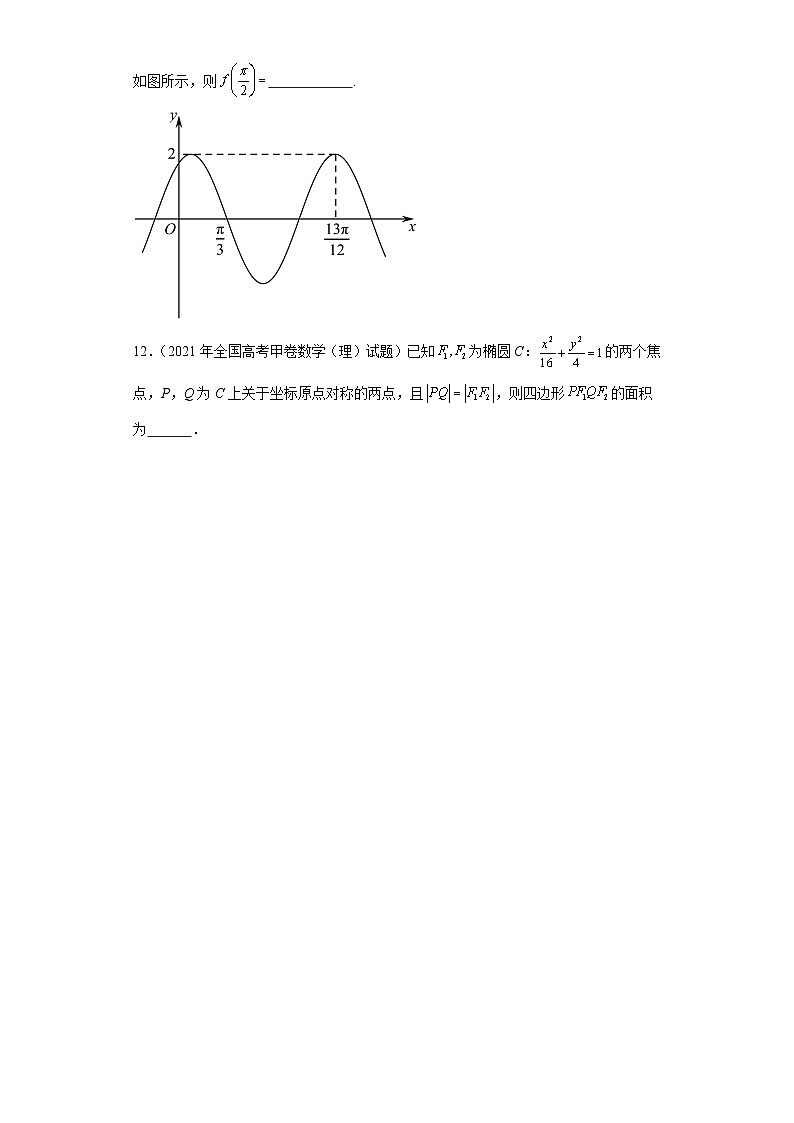
11．（2021年全国高考甲卷数学（文）试题）已知函数的部分图像如图所示，则 .

12．（2021年全国高考甲卷数学（理）试题）已知为椭圆C：的两个焦点，P，Q为C上关于坐标原点对称的两点，且，则四边形的面积为 ．

参考答案：
1．
【分析】先分析，再由等比数列的前项和公式和平方差公式化简即可求出公比.
【详解】若，
则由得，则，不合题意.
所以.
当时，因为，
所以，
即，即，即，
解得.
故答案为：
2．2
【分析】利用偶函数的性质得到，从而求得，再检验即可得解.
【详解】因为为偶函数，定义域为，
所以，即，
则，故，
此时，
所以，
又定义域为，故为偶函数，
所以.
故答案为：2.
3．15
【分析】由约束条件作出可行域，根据线性规划求最值即可.
【详解】作出可行域，如图，
  
由图可知，当目标函数过点时，有最大值，
由可得，即,
所以.
故答案为：15
4．
【分析】当球是正方体的外接球时半径最大，当边长为的正方形是球的大圆的内接正方形时半径达到最小.
【详解】设球的半径为.
当球是正方体的外接球时，恰好经过正方体的每个顶点，所求的球的半径最大，若半径变得更大，球会包含正方体，导致球面和棱没有交点，
正方体的外接球直径为体对角线长，即，故；
  
分别取侧棱的中点，显然四边形是边长为的正方形，且为正方形的对角线交点，
连接，则，当球的一个大圆恰好是四边形的外接圆，球的半径达到最小，即的最小值为.
综上，.
故答案为：
5．/
【分析】直接由向量垂直的坐标表示求解即可.
【详解】由题意知：，解得.
故答案为：.

6．
【分析】设出点M的坐标，利用和均在上，求得圆心及半径，即可得圆的方程.
【详解】[方法一]：三点共圆
∵点M在直线上，
∴设点M为，又因为点和均在上，
∴点M到两点的距离相等且为半径R，
∴，
，解得，
∴，，
的方程为.
故答案为：
[方法二]：圆的几何性质
由题可知，M是以（3，0）和（0，1）为端点的线段垂直平分线 y=3x-4与直线的交点(1,-1)., 的方程为.
故答案为：

7．2（满足皆可）
【分析】根据题干信息，只需双曲线渐近线中即可求得满足要求的e值.
【详解】解：，所以C的渐近线方程为,
结合渐近线的特点，只需，即，
可满足条件“直线与C无公共点”
所以，
又因为，所以，
故答案为：2（满足皆可）

8．/
【分析】设，利用余弦定理表示出后，结合基本不等式即可得解.
【详解】[方法一]：余弦定理
设，
则在中，，
在中，，
所以
，
当且仅当即时，等号成立，
所以当取最小值时，.
故答案为：.


[方法二]：建系法
令 BD=t，以D为原点，OC为x轴，建立平面直角坐标系.
则C（2t,0），A（1，），B（-t,0）

[方法三]：余弦定理
设BD=x,CD=2x.由余弦定理得
，，
，，
令，则，
，
，
当且仅当，即时等号成立.
[方法四]：判别式法
设，则
在中，，
在中，，
所以，记，
则
由方程有解得：
即，解得：
所以，此时
所以当取最小值时，，即.
   
9．
【分析】根据题目条件，利用模的平方可以得出答案
【详解】∵
∴
∴.
故答案为：.
10．
【分析】利用体积公式求出圆锥的高，进一步求出母线长，最终利用侧面积公式求出答案.
【详解】∵
∴
∴
∴.
故答案为：.

11．
【分析】首先确定函数的解析式，然后求解的值即可.
【详解】由题意可得：，
当时，，
令可得：，
据此有：.
故答案为：.
【点睛】已知f(x)＝Acos(ωx＋φ)(A＞0，ω＞0)的部分图象求其解析式时，A比较容易看图得出，困难的是求待定系数ω和φ，常用如下两种方法：
(1)由ω＝即可求出ω；确定φ时，若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x0，则令ωx0＋φ＝0(或ωx0＋φ＝π)，即可求出φ.
(2)代入点的坐标，利用一些已知点(最高点、最低点或“零点”)坐标代入解析式，再结合图形解出ω和φ，若对A，ω的符号或对φ的范围有要求，则可用诱导公式变换使其符合要求.
12．
【分析】根据已知可得，设，利用勾股定理结合，求出，四边形面积等于，即可求解.
【详解】因为为上关于坐标原点对称的两点，
且，所以四边形为矩形，
设，则，
所以，
，即四边形面积等于.
故答案为：.