




浙教版数学七上第二章《有理数的运算》单元能力提升卷(困难)
展开浙教版数学七上 第二章 《有理数的运算》单元能力提升卷
一.选择题(共30分)
1.如果a、b是有理数,则下列各式子成立的是( )
A.如果a<0,b<0,那么a+b>0
B.如果a>0,b<0,那么a+b>0
C.如果a>0,b<0,那么a+b<0
D.如果a<0,b>0,且|a|>|b|,那么a+b<0
2.m是有理数,则m+|m|( )
A.可以是负数 B.不可能是负数
C.一定是正数 D.可是正数也可是负数
3.有理数a、b、c在数轴上对应点的位置如图所示,若|b|>|c|,则下列结论中正确的是( )
![]()
A.abc<0 B.b+c<0 C.a+c>0 D.ac>ab
4.已知![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]()
5.有理数m,n在数轴上的位置如图所示,则下列关系式中正确的有( )
①m+n<0;②n﹣m>0;③n>0;④m>0.
![]()
A.1个 B.2个 C.3个 D.4个
6.已知a=﹣![]() ,b=
,b=![]() ,c=﹣
,c=﹣![]() ,则下列各式结果最大的是( )
,则下列各式结果最大的是( )
A.|a+b+c| B.|a+b﹣c| C.|a﹣b+c| D.|a﹣b﹣c|
7.根据一周7天可以制作出每年的“星期几密码”.现已知2035年的“星期几密码”是“033 614 625 035”,这组密码中从左到右的12个数字依次与2035年的1到12月对应,我们可以用这组密码算出2035年某天是星期几.如2035年2月8日,其中2月对应密码中的第二个数字“3”,将数字3加上日期8,其和为11,再把11除以7,得余数4,则该天为星期四(余数几则对应星期几,特别地,余数0则对应星期天).利用此密码算出2035年的世界环境日(6月5日)是( )
A.星期一 B.星期二 C.星期四 D.星期六
8.下列说法:![]() 和
和![]() 互为相反数;
互为相反数;![]() 绝对值等于它本身的数是
绝对值等于它本身的数是![]() 、
、![]() ;
;![]() 若
若![]() 则
则![]() 、
、![]() 为相反数;
为相反数;![]() 读作“
读作“![]() 的
的![]() 次幂”
次幂”![]() 近似数
近似数![]() 万精确到十分位;
万精确到十分位;![]() 若
若![]() 是有理数,则它的相反数是
是有理数,则它的相反数是![]() ,倒数是
,倒数是![]() ;下列说法正确的是( )
;下列说法正确的是( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
9.现有四种说法:
①几个有理数相乘,当负因数有奇数个时,积为负;
②几个有理数相乘,积为负时,负因数有奇数个;
③当x<0时,|x|=﹣x;
④当|x|=﹣x时,x<0.
其中正确的说法是( )
A.②③ B.③④ C.②③④ D.①②③④
10.下列结论:①一个数和它的倒数相等,则这个数是±1和0;②若﹣1<m<0,则m<m2<![]() ;③若a+b<0,且
;③若a+b<0,且![]() ,则|a+2b|=﹣a﹣2b;④若m是有理数,则|m|+m是非负数;⑤若c<0<a<b,则(a﹣b)(b﹣c)(c﹣a)>0;其中正确的有( )
,则|a+2b|=﹣a﹣2b;④若m是有理数,则|m|+m是非负数;⑤若c<0<a<b,则(a﹣b)(b﹣c)(c﹣a)>0;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共24分)
11.近几年宁波市常住人口总量持续增长,根据第七次全国人口普查数据显示宁波市常住人口约为![]() 万人,
万人,![]() 万精确到 位
万精确到 位
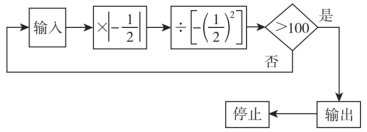
12.按如图所示的程序进行计算,如果第一次输入的数是20,而结果不大于100时,应把结果作为输入的数再进行第二次运算,直到符合要求为止,则最后输出的结果为________.
13.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…通过观察,用所发现的规律确定215的个位数字是 .
14.我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2,(1011)2换算成十进制数应为:
![]() ;
;![]()
按此方式,将二进制(1101)2换算成十进制数的结果是 13 .
15.已知整数a,b,c,d的绝对值均小于5,且满足![]() ,则
,则![]() 的值为_______.
的值为_______.
16.如图,已知点A、点B是直线上的两点,![]() 厘米,点C在线段AB上,且
厘米,点C在线段AB上,且![]() 厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发在直线上运动,则经过______秒时线段PQ的长为8厘米.
厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发在直线上运动,则经过______秒时线段PQ的长为8厘米.
![]()
三.解答题(共66分)
17.(8分)计算:
(1)(+16)﹣(+11)﹣(﹣18)+(﹣15); (2)﹣12﹣(1﹣0.5)÷![]() ;
;
(3)![]() ; (4)
; (4)![]()
18.(6分)食品厂为检测某袋装食品的质量是否符合标准,从袋装食品中抽出样品30袋,每袋以100克为标准质量,超过和不足100克的部分分别用正、负数表示,记录如下:
与标准质量的差值/克 | -4 | -2 | 0 | 1 | 2 | 3 |
袋数 | 3 | 4 | 6 | 8 | 6 | 3 |
(1)在抽测的样品中,任意挑选两袋,它们的质量最大相差多少克?
(2)食品袋中标有“净重![]() 克”,这批抽样食品中共有几袋质量合格?请你计算出这30袋食品的合格率;(3)这批样品的平均质量比每袋的标准质量多(或少)多少克?
克”,这批抽样食品中共有几袋质量合格?请你计算出这30袋食品的合格率;(3)这批样品的平均质量比每袋的标准质量多(或少)多少克?
19.(8分)对于有理数a,b,n,d,若![]() ,则称a和b关于n的“相对关系值”为d,例如:
,则称a和b关于n的“相对关系值”为d,例如:![]() ,则2和3关于1的“相对关系值”为3.
,则2和3关于1的“相对关系值”为3.
(1)![]() 和5关于1的“相对关系值”为__________.
和5关于1的“相对关系值”为__________.
(2)若a和2关于3的“相对关系值”为10,求a的值.
20.(10分)一个四位正整数的千位、百位、十位、个位上的数字分别为a,b,c,d,如果![]() ,那么我们把这个四位正整数叫做“进步数”,例如四位正整数1234:因为
,那么我们把这个四位正整数叫做“进步数”,例如四位正整数1234:因为![]() ,所以1234叫做“进步数”.
,所以1234叫做“进步数”.
(1)写出四位正整数中的最大的“进步数”与最小的“进步数”;
(2)已知一个四位正整数m是“进步数”,m的千位、个位上的数字分别是1、8,且m能被9整除,求这个四位正整数m.
21.(10分)先阅读后解题.
已知![]() ,求
,求![]() 和
和![]() 的值.
的值.
解:把等式的左边分解因式:![]() .
.
即![]() .
.
因为![]() ,
,![]() .
.
所以![]() ,
,![]() 即
即![]() ,
,![]() .
.
利用以上解法,解下列问题:![]() 已知:
已知:![]() ,求
,求![]() 和
和![]() 的值.
的值.![]() 已知
已知![]() ,
,![]() ,
,![]() 是
是![]() 的三边长,满足
的三边长,满足![]() 且
且![]() 为等腰三角形,求
为等腰三角形,求![]() .
.
22.(12分)问题探索:如图,将一根木棒放在数轴(单位长度为1cm)上,木棒左端与数轴上的点A重合,右端与数轴上的点B重合.
![]()
(1)若将木棒沿数轴向右水平移动,则当它的左端移动到点B时,它的右端在数轴上所对应的数为30;若将木棒沿数轴向左水平移动,则当它的右端移动到点A时,它的左端在数轴上所对应的数为6,由此可得这根木棒的长为 cm.
(2)图中点A所表示的数是 ,点B所表示的数是 .
实际应用:由(1)(2)的启发,请借助“数轴”这个工具解决下列问题:
(3)一天,妙妙去问奶奶的年龄,奶奶说:“我若是你现在这么大,你还要35年才出生;你若是我现在这么大,我就115岁啦! ”请问妙妙现在多少岁了?
23.(12分)我们知道:在分析和研究数学问题时,当问题所述对象不能进行统一研究时,我们就需要根据数学对象的本质属性,将对象区分为不同种类,然后逐类进行分析和研究,最后综合各类结果得到整个问题的答案,这一思想方法,我们称之为“分类讨论思想”。这一数学思想用处非常广泛,我们经常用这种方法解决问题,例如:我们在讨论![]() 的值时,就会对
的值时,就会对![]() 进行分类讨论:当
进行分类讨论:当![]() ;当
;当![]()
![]() ___________,
___________,![]() ___________.
___________.
![]() ___________
___________![]() ,
,![]() ___________
___________![]() .
.
![]() 若
若![]() ,试求
,试求![]() 的所有可能的值.
的所有可能的值.









