数学第3章 图形的相似3.1 比例线段试讲课ppt课件

这是一份数学第3章 图形的相似3.1 比例线段试讲课ppt课件，共16页。PPT课件主要包含了新课导入，探究新知，即使得，巴台农神庙，泰姬陵，课堂练习，课堂小结等内容，欢迎下载使用。
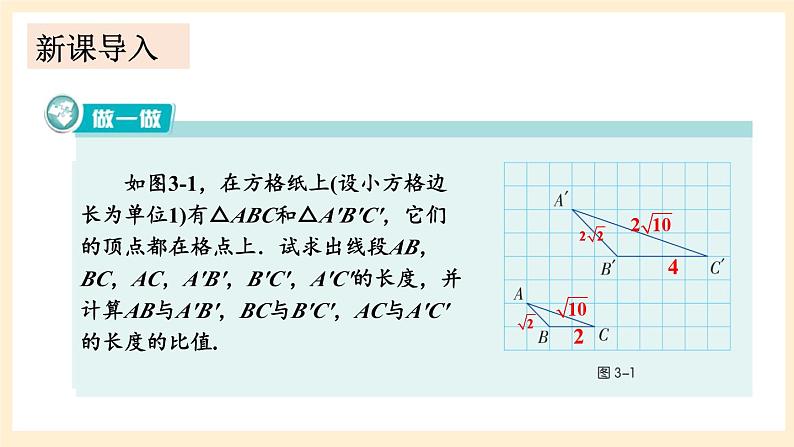
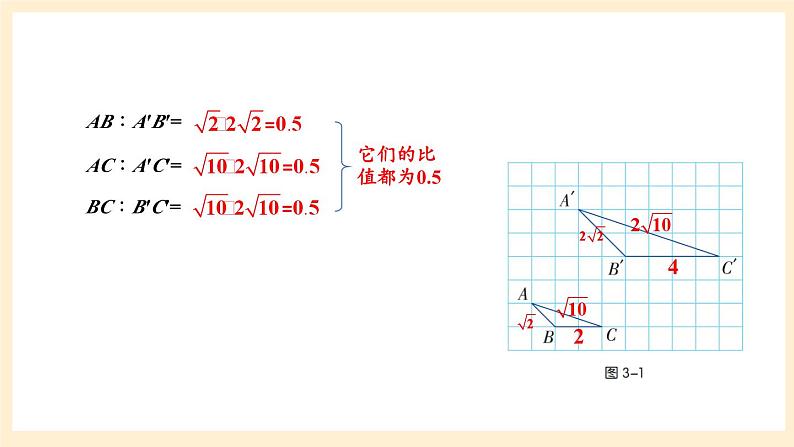
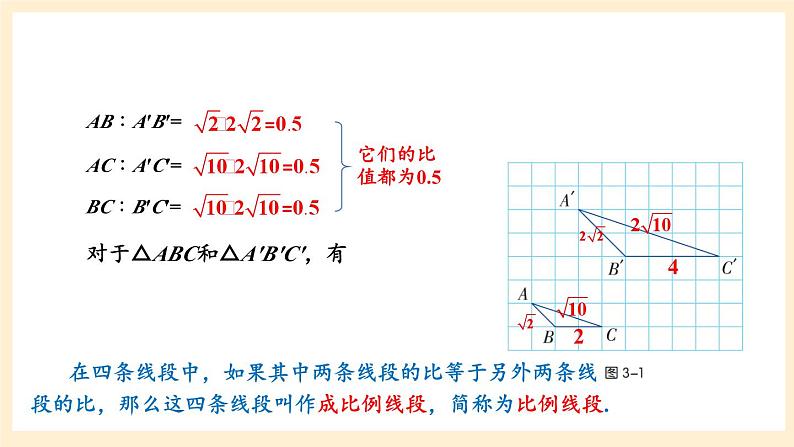
如图3-1，在方格纸上(设小方格边长为单位1)有△ABC和△A'B'C'，它们的顶点都在格点上．试求出线段AB，BC，AC，A'B'，B'C'，A'C'的长度，并计算AB与A'B'，BC与B'C'，AC与A'C'的长度的比值.
对于△ABC和△A′B′C′，有
在四条线段中，如果其中两条线段的比等于另外两条线段的比，那么这四条线段叫作成比例线段，简称为比例线段.
已知四条线段a，b，c，d，若 ，则a，b，c，d是比例线段.
类似地，如果 ，那么称线段AB，BC，AC与线段A′B′ ，B′C′ ，A′C′对应成比例.
已知线段a，b，c，d的长度分别为0.8cm，2cm，1.2cm，3cm，问a，b，c，d是比例线段吗？
古希腊数学家、天文学家欧多克索斯（Eudxus，约前400—约前347）曾经提出一个问题：
能否将一条线段AB分成不相等的两部分，使较短线段CB与较长线段AC的比等于线段AC与原线段AB的比？
根据 ，列出方程
视觉生理学的研究成果表明，符合黄金分割的比例形式很容易使人产生视觉上的美感.许多世界著名古建筑物中都包含有“黄金分割比”，例如古希腊的巴台农神庙、印度泰姬陵、法国巴黎圣母院这些著名建筑的正面高度与底部宽度之比均约为黄金分割比.
在现代，许多建筑的设计中也采用了黄金分割，例如，上海的东方明珠广播电视塔的上球体就处于整个塔身高度的黄金分割处. 神奇的“黄金分割比”也出现在许多著名艺术作品中，如在意大利著名画家达·芬奇的名作《蒙娜丽莎》中，人物的脸的宽度与高度的比就是一个黄金分割比.
1.已知a，b，c，d是比例线段.
（1）若a=0.8cm，b=1cm，c=1cm，求d；
（2）若a=12cm，c=3cm，d=15cm，求b；
（3）若a=5cm，b=4cm，d=8cm，求c.
2.在比例尺1∶1000000的地图上，量得A，B两地的距离是25cm.求A，B两地之间的实际距离.
答：AB两地之间的实际距离是250km.
一般地，如果选用同一长度单位量得两条线段AB，A′B′的长度分别为m，n，那么把它们的长度的比 叫作这两条线段AB与A′B′的比，记作