湘教版数学九上 第3章《图形的相似章末复习》课件

这是一份湘教版数学九上 第3章《图形的相似章末复习》课件，共32页。

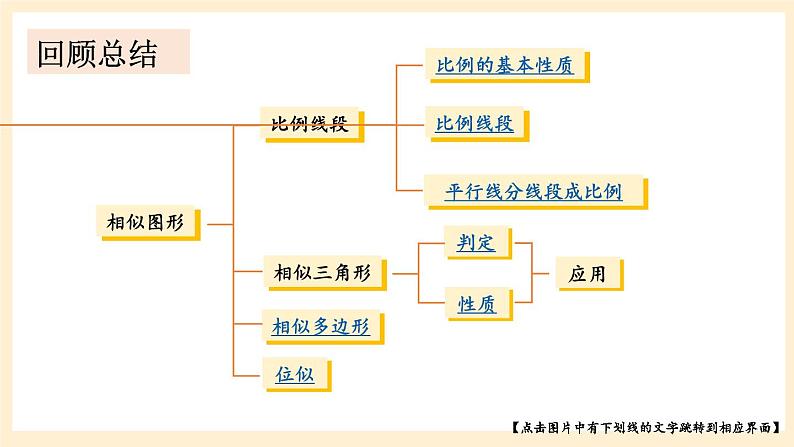
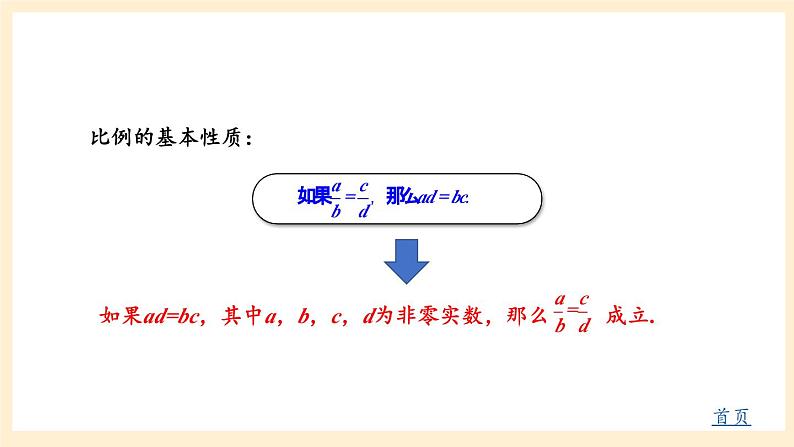
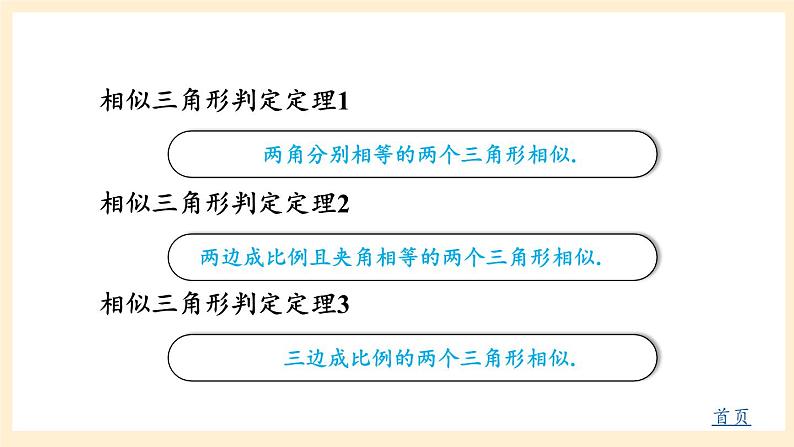
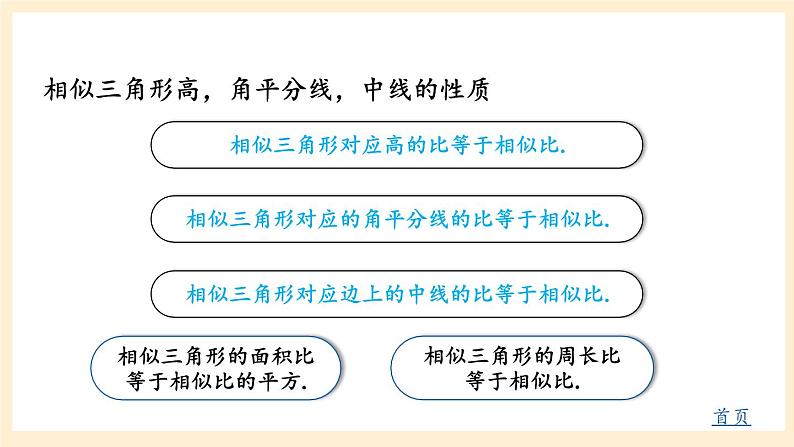
湘教版数学九年级上册 第3章《图形的相似章末复习》【点击图片中有下划线的文字跳转到相应界面】回顾总结比例的基本性质：首页已知四条线段a，b，c，d中，若 ，则a，b，c，d是比例线段. 类似地，如果 ，那么称线段AB，BC，AC与线段A′B′ ，B′C′ ，A′C′对应成比例. 黄金分割比为 ，它约等于0.618.比例线段首页平行线分线段成比例首页相似三角形判定定理1相似三角形判定定理2相似三角形判定定理3首页相似三角形高，角平分线，中线的性质首页 对于两个边数相同的多边形，如果他们的对应角相等，对应边成比例，那么这两个多边形叫作相似多边形.相似多边形的对应边的比也叫作相似比.相似多边形首页位似首页 一般地，取定一个点O，如果一个图形G上每一个点P对应于另一个图形G′上的点P′，且满足： 那么称图形G与图形G′是位似图形.这个点O叫作位似中心，常数k叫作位似比.（1）直线PP′经过点O，A 组课堂练习∵DE=6，∴EF=4.∴DF=DE+EF=4+6=10.解：∵l1∥l2∥l3，解：∵∠C=∠D=90°， ∠CAB=∠DAE，∴△ACB∽△ADE.∵CB=9.8m，AC=14.2m，AD=28.4m，∴ED=19.6m.证明：∵AC=5，BC=3，EC=10，DC=6，∴△ACB∽△ECD，∴AB∥DE.又∠ACB=∠ECD，∴∠A=∠E，∵AB=14km，AD=28km，BD=21km，BC=42km，DC=31.5km∴△ABD∽△BDC，∴AB∥DC.∴∠ABD=∠BDC，解：平行，理由如下：∴△DEF面积为56.25∴△DEF周长为24解：∵∠1=∠2，∴∠CED=∠AEB，又∠CDE=∠ABE=90°，∴△CED∽△AEB，∵DE=3m，CD=1.5m，BE=8m，∴AB=4m.答：树AB的高度为4m.∴BE=55.2m答：此时他与教学楼的距离BE为55.2m.M解：过点F作FM⊥DC于M，交AB于点N.易得△AFN∽△DFM，NA′B′C′D′A′′B′′C′′D′′是位似图形.A′B′C′D′A′′B′′C′′D′′是位似图形.B 组证明 :（1）∵CD是斜边AB上的高，∴∠ADC=90°，在△ACB和△ADC中，∴△ACB∽△ADC，在△ACB和△ADC中，∵∠ACB=∠ADC=90°，∠A=∠A，（2）在Rt△ABC中，∵∠ACB=90°，∴∠A+∠B=90°，∵CD⊥AB，∴ △BDC∽△CDA，∴∠B+∠BCD=90°，∴∠A=∠BCD，又∠BDC=∠CDA，解：∵AE∥DB，∴△BCD∽△ACE，∵DE=2.7m，CE=8.7m，AB=1.8m，∴BC=4m.答：窗口底边离地面的高是4m.当△ABE∽△NDM，解：四边形A′B′C′D′与四边形ABCD相似，理由如下：且AA′， BB′， CC′， DD′，都经过同一个点O，∴四边形A′B′C′D′与四边形ABCD是位似图形，故可得四边形A′B′C′D′∽四边形ABCD.（-2,4）（-4,0）（2,4）（4,-2）（2,-6）（-2,-4）C 组解：能，过点P作PH⊥AB交直线AB于点H，则有PH∥EF，PH∥CD.设PH=hm，FH=xm.在△BFE和△BHP中，∵∠BFE=∠BHP=90°，∠EBF=∠PBH，∴△BFE∽△BHP，同理可得△ADC∽△AHP，H答：支架顶端Р到地面的距离约为8.3m.1.从课后习题中选取；2.完成练习册本课时的习题.课后作业