湘教版数学九上 4.1《 正弦和余弦》第2课时 45°，60°角的正弦值及用计算器求正弦值或锐角 课件

这是一份湘教版数学九上 4.1《 正弦和余弦》第2课时 45°，60°角的正弦值及用计算器求正弦值或锐角 课件，共16页。

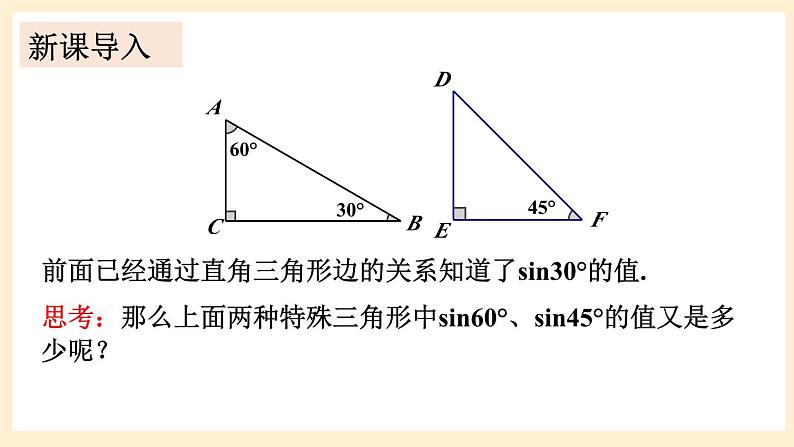
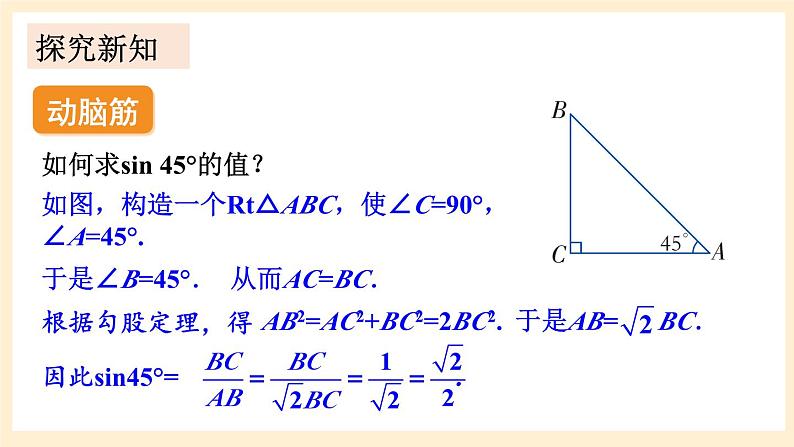
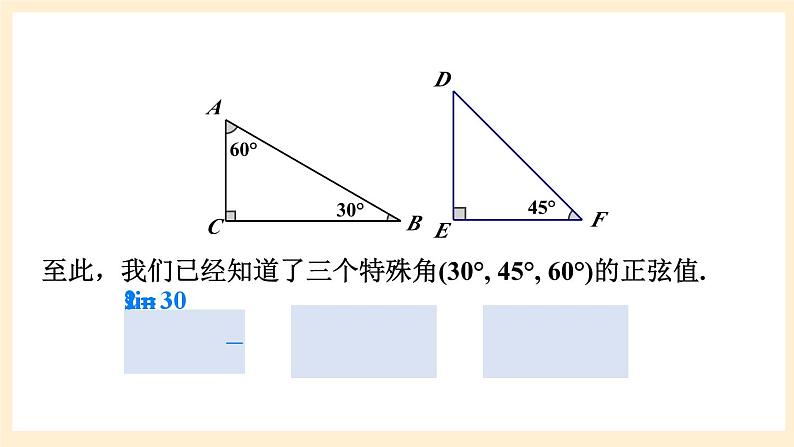
湘教版数学九年级上册4.1.2 45°，60°角的正弦值及用计算器求正弦值或锐角前面已经通过直角三角形边的关系知道了sin30°的值.思考：那么上面两种特殊三角形中sin60°、sin45°的值又是多少呢？30°60°45°ACBDEF新课导入动脑筋如何求sin 45°的值？如图，构造一个Rt△ABC，使∠C=90°，∠A=45°.于是∠B=45°．从而AC=BC．根据勾股定理，得AB2=AC2+BC2=2BC2.于是AB= BC．因此sin45°= .探究新知如何求sin 60°的值？如图所示，构造一个Rt△ABC ，使∠B=60°，则∠A=30°.30°60°45°ACBDEF至此，我们已经知道了三个特殊角(30°, 45°, 60°)的正弦值.对于一般锐角α的正弦值，我们可以利用计算器来求．用计算器求锐角的正弦值要用到sin键. 如果已知正弦值，我们也可以利用计算器求出它的对应锐角. 例如，已知sinα=0.7071，依次按键显示结果为44.999…，表示角α约等于45°.做一做利用计算器计算：（1）sin40°≈ ______________（精确到0.0001）；（2）sin15°30′≈ ______________（精确到0.0001）；（3）若sin α=0.522 5，则 α ≈ ____________（精确到0.1°）；（4）若sin α=0.809 0，则 α ≈ ____________（精确到0.1°）.0.64280.267231.5°54.0 °例2：计算：解：小 结：1.直角三角形中，角α的正弦函数等于哪两边之比呢？2.直角三角形中，sin α值的范围是什么？3.学习角α的正弦函数时，用到了什么主要的数学思想方法？练习1.用计算器求下列锐角的正弦值（精确到0.0001）：（1）35°； （2）65°36′； （3）80°54′.解：（1）sin35°=0.5736；（2）sin65°36′=0.9107；（3）sin80°54′=0.9874.课堂练习2.已知下列正弦值，用计算器求对应的锐角(精确到0.1°)：（1）sin α =0.8071； （2）sin α =0.8660.解：（1）α ≈ 53.8°；（2）α ≈ 60.0°；3.计算：（1） sin260°+sin245°； （2） 1-2sin30°sin60°.解：sin260°+sin245°解：1-2sin30°sin60°4.如图，一名患者体内某器官后面有一肿瘤，在接受放射性治疗时，为了最大限度地保证疗效，并且防止伤害器官，射线必须从侧面照射肿瘤，已知肿瘤在皮下6.3cm的A处，射线从肿瘤右侧9.8cm的B处进入身体，求∠CBA的度数.解：在Rt△ABC中，由勾股定理可得 AB2= AC2+BC2= 6.32+9.82=135.73.于是AB≈11.65.则∠CAB≈32°44′.30°60°45°ACBDEF课堂小结1.从课后习题中选取；2.完成练习册本课时的习题.课后作业