人教版九年级上册第二十二章 二次函数22.3 实际问题与二次函数精品随堂练习题

这是一份人教版九年级上册第二十二章 二次函数22.3 实际问题与二次函数精品随堂练习题，文件包含人教版数学九年级上册223《实际问题与二次函数几何图形面积最值》作业解析版docx、人教版数学九年级上册223《实际问题与二次函数几何图形面积最值》作业原卷版docx等2份试卷配套教学资源，其中试卷共43页， 欢迎下载使用。

22.3实际问题与二次函数—几何图形面积最值（作业）
（夯实基础+能力提升）
【夯实基础】
一、单选题
1．（2022·全国·九年级课时练习）已知关于x的方程的两个根分别是-1和3，若抛物线与y轴交于点A，过A作轴，交抛物线于另一交点B，则AB的长为（    ）
A．2 B．3 C．1 D．1.5
【答案】A
【分析】根据方程的两根求出b、c的值，代入抛物线解析式，求出点A坐标，A、B两点纵坐标相同，从而求出B点坐标，AB的长即可求出．
【详解】将-1，3分别代入，
，
解得，
∴抛物线解析式为：，
∴与y轴交点为：A（0，6），
∵AB⊥y轴，∴B的纵坐标为6，
代入抛物线解得，，
∴B（2，6）
∴AB=2-0=2．
故选：A．
【点睛】本题考查了抛物线与y轴的交点，根与系数的关系，二次函数图象上点的坐标特征，掌握根与系数的关系是解题的关键．
2．（2022·江苏·九年级专题练习）如图，用绳子围成周长为的矩形，记矩形的一边长为，矩形的面积为．当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数表达式为（    ）

A． B．
C． D．
【答案】A
【分析】矩形的周长为2（x+y）＝10，可用x来表示y，代入S＝xy中，化简即可得到S关于x的函数关系式．
【详解】解：由题意得，
2（x+y）＝10，
∴x+y＝5，
∴y＝5﹣x，
∵S＝xy
＝x（5﹣x）
∴矩形面积满足的函数关系为S＝x（5﹣x），
由题意可知自变量的取值范围为，
故选：A．
【点睛】本题考查了二次函数在实际问题中的应用，理清题中的数量关系并熟练掌握二次函数的解析式形式是解题的关键．
3．（2022·全国·九年级课时练习）如图，用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD，设AB边长为x米，BC的长y米，菜园的面积为S(单位：平方米) ．当x在一定范围内变化时，y和S都随x的变化而变化，则y与x，S与x满足的函数关系分别是（    ）

A．一次函数关系，二次函数关系 B．反比例函数关系，二次函数关系
C．一次函数关系，反比例函数关系 D．反比例函数关系，一次函数关系
【答案】A
【分析】根据题意求得y和S与x的函数关系式，然后由函数关系式可直接进行判别即可．
【详解】解：由题意可知：，
，则，即，y与x满足一次函数关系
菜园的面积：，S与x满足二次函数的关系
故选A
【点睛】本题主要考查一次函数与二次函数的应用，熟练掌握一次函数与二次函数的应用是解题的关键．
4．（2022·全国·九年级单元测试）长为，宽为的矩形，四个角上剪去边长为的小正方形，然后把四边折起来，作成底面为的无盖的长方体盒子，则y与x的关系式为（    ）
A． B．
C． D．
【答案】C
【分析】利用现有一块长20cm、宽10cm的矩形，将它的四个角各剪去一个边长为xcm的小正方形，则底面长与宽均减少2xcm，表示出无盖的长方体盒子底边的长，进而得出y与x之间的函数关系式．
【详解】解：设小正方形边长为xcm，由题意知：
现在底面长为（20-2x）cm，宽为（10-2x）cm，
则y=（10-2x）（20-2x）（0＜x＜5），
故选：C．
【点睛】此题主要考查了根据实际问题列二次函数关系式，表示出长方体盒子底边的长与宽是解题关键．
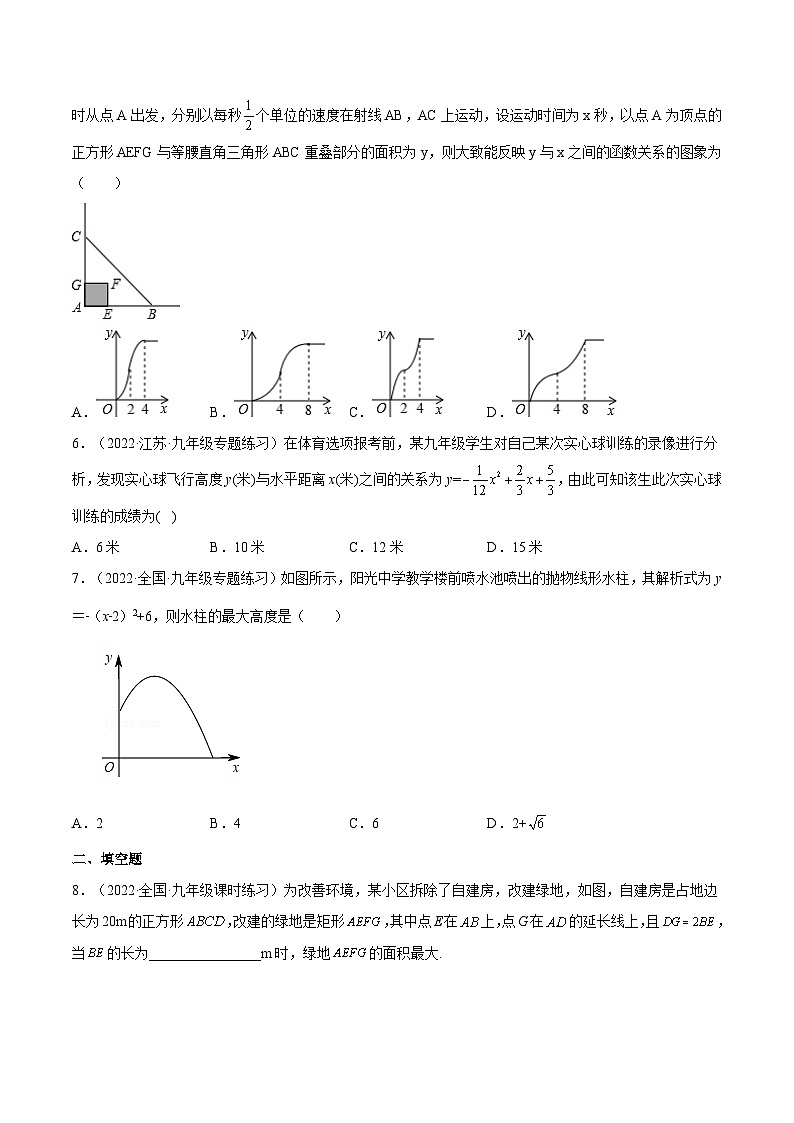
5．（2022·全国·九年级专题练习）如图，在等腰直角三角形ABC中，∠BAC=90°，AB=AC=4，点E，G同时从点A出发，分别以每秒个单位的速度在射线AB，AC上运动，设运动时间为x秒，以点A为顶点的正方形AEFG与等腰直角三角形ABC重叠部分的面积为y，则大致能反映y与x之间的函数关系的图象为（　　）

A． B． C． D．
【答案】B
【分析】分0＜x≤4、4＜x≤8、x＞8三个时间段求出函数解析式即可确定其图象.
【详解】解：①当0＜x≤4时，y=x2，
②当4＜x≤8时，y=×4×4-2××（4-x）2=x2+4x-8，
③当x＞8时，y=8，
故选：B．
【点睛】本题考查了动点问题中有关图形面积的函数图象，灵活的表示出图形的面积与动点运动时间的函数关系是解题的关键.
6．（2022·江苏·九年级专题练习）在体育选项报考前，某九年级学生对自己某次实心球训练的录像进行分析，发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=，由此可知该生此次实心球训练的成绩为(   )
A．6米 B．10米 C．12米 D．15米
【答案】B
【分析】根据铅球落地时，高度y=0，把实际问题理解为当y=0时，求x的值即可；
【详解】铅球落地时高度为0，即当y=0时，
=0，
解得x1=10，x2=-2（舍去），
所以该生此次实心球训练的成绩为10米，
故选：B．
【点睛】本题考查了二次函数的应用中，函数式中自变量与函数表达的实际意义，需要结合题意，取函数或自变量的特殊值列方程求解是解题关键．
7．（2022·全国·九年级专题练习）如图所示，阳光中学教学楼前喷水池喷出的抛物线形水柱，其解析式为y＝﹣（x﹣2）2+6，则水柱的最大高度是（　　）

A．2 B．4 C．6 D．2+
【答案】C
【分析】根据二次函数的性质，在顶点处取最值即可．
【详解】解：∵抛物线形水柱，其解析式为y＝﹣（x﹣2）2+6，
∵a=-1＜0
∴当x=2时，水柱的最大高度是：6．
故选C．
【点睛】本题考查二次函数的实际应用—喷水问题．根据二次函数的解析式得到抛物线顶点坐标是解决此类问题的关键．

二、填空题
8．（2022·全国·九年级课时练习）为改善环境，某小区拆除了自建房，改建绿地，如图，自建房是占地边长为20m的正方形，改建的绿地是矩形，其中点E在上，点G在的延长线上，且，当的长为________________m时，绿地的面积最大.

【答案】5
【分析】设的长为x，得到，，根据面积公式列出二次函数即可求解.
【详解】设的长为x，则，，
∴，
∵矩形绿地的面积为：，
即矩形绿地的面积为，
∴当时，矩形绿地的面积最大.
故答案为：5.
【点睛】此题主要考查二次函数的应用，解题的关键是根据题意列出函数进行求解.
9．（2022·全国·九年级单元测试）根据物理学规律，如果不考虑空气阻力，以的速度将小球沿与地面成角的方向击出，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间的函数关系是，当飞行时间t为___________s时，小球达到最高点．
【答案】2
【分析】将函数关系式转化为顶点式即可求解．
【详解】根据题意，有，
当时，有最大值．
故答案为：2．
【点睛】本题考查二次函数解析式的相互转化及应用，解决本题的关键是熟练二次函数解析式的特点及应用．
10．（2022·全国·九年级课时练习）如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线．若不考虑空气阻力，小球的飞行高度（单位：m）与飞行时间（单位：s）之间具有函数关系：，则当小球飞行高度达到最高时，飞行时间_________s．

【答案】2
【分析】把一般式化为顶点式，即可得到答案．
【详解】解：∵h=-5t2+20t=-5（t-2）2+20，
且-5＜0，
∴当t=2时，h取最大值20，
故答案为：2．
【点睛】本题考查二次函数的应用，解题的关键是掌握将二次函数一般式化为顶点式．
11．（2022·江苏·九年级专题练习）某广场有一喷水池，水从地面喷出，如图，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线（单位：米）的一部分，则水喷出的最大高度是__________米．

【答案】4
【分析】将一般式写成顶点式，求出顶点坐标即可得出结果．
【详解】∵，
∴顶点坐标是(2，4)，
∴最大高度是4米．
故答案为：4．
【点睛】本题考查二次函数的实际应用，解题的关键是掌握求二次函数图象顶点坐标的方法．

三、解答题
12．（2022·全国·九年级专题练习）园林部门计划在某公园建一个长方形苗圃．苗圃的一面靠墙（墙最大可用长度为14米）．另三边用木栏围成，中间也用垂直于墙的木栏隔开，分成两个区域，并在如图所示的两处各留2米宽的门（门不用木栏），建成后所用木栏总长32米，设苗圃的一边长为x米．

(1)长为________米（包含门宽，用含x的代数式表示）；
(2)若苗圃的面积为，求x的值；
(3)当x为何值时，苗圃的面积最大，最大面积为多少？
【答案】(1)（36-3x）
(2)8
(3)当x为米时，苗圃ABCD的最大面积为平方米

【分析】（1）根据木栏总长32米，两处各留2米宽的门，设苗圃的一边长为x米，即得BC的长为（36-3x）米；（2）根据题意得，，即可解得x的值；（3）设苗圃的面积为w，，由二次函数的性质可得答案．
（1）
∵木栏总长32米，两处各留2米宽的门，设苗圃的一边长为x米，
BC的长为32-3x+4=（36-3x）米，
故答案为：（36-3x）；
（2）
根据题意得，，
解得，x=4或x=8，
∵当x=4时，36-3x=24>14，
∴x=4舍去，
∴x的值为8；
（3）
设苗圃的面积为w，
，
∵4<36-3x14，
∴，
∵-3<0，图象开口向下，
∴当时，w取得最大值，w最大为；
答：当x为米时，苗圃ABCD的最大面积为平方米．
【点睛】本题考查了二次函数的应用，解题的关键是读懂题意，根据已知列方程和函数关系式．
13．（2022·全国·九年级专题练习）如图，ABCD是一块边长为4米的正方形苗圃，园林部门拟将其改造为矩形AEFG的形状，其中点E在AB边上，点G在AD的延长线上，DG = 2BE．设BE的长为x米，改造后苗圃AEFG的面积为y平方米．

（1）求y与x之间的函数关系式（不需写自变量的取值范围）；
（2）根据改造方案，改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等，请问此时BE的长为多少米？
【答案】（1）y=-2x+4x+16；（2）2米
【分析】（1）若BE的长为x米，则改造后矩形的宽为米，长为米，求矩形面积即可得出y与x之间的函数关系式；
（2）根据题意可令函数值为16，解一元二次方程即可．
【详解】解：（1）∵BE边长为x米，
∴AE=AB-BE=4-x，AG=AD+DG=4+2x    
苗圃的面积=AE×AG=(4-x)(4+2x)
则苗圃的面积y（单位：米2）与x（单位：米）的函数关系式为：y=-2x+4x+16
（2）依题意，令y=16  即-2x+4x+16=16
解得：x=0(舍）x=2
答：此时BE的长为2米．
【点睛】本题考查的知识点是列函数关系式以及二次函数的实际应用，难度不大，找准题目中的等量关系式是解此题的关键．
14．（2022·全国·九年级专题练习）某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同。如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C、D为水柱的落水点，水柱所在抛物线(第一象限部分)的函数表达式为．

(1)求落水点C、D之间的距离；
(2)若需在OD上离O点10米的E处竖立雕塑EF，，且雕塑的顶部刚好碰到水柱，求雕塑EF的高．
【答案】(1)22米
(2)雕塑EF的高为米

【分析】（1）利用二次函数图象上点的坐标特征可求出点D的坐标，进而可得出OD的长度，由喷出的水柱为抛物线且形状相同，可得出OC的长，结合CD＝OC+OD即可求出落水点C，D之间的距离；
（2）代入x＝10求出y值即可．
（1）
解：当y＝0时，，
解得：x1＝﹣1（舍去），x2＝11，
∴点D的坐标为（11，0），
∴OD＝11m．
∵从A点向四周喷水，喷出的水柱为抛物线，且形状相同，
∴OC＝OD＝11m，
∴CD＝OC+OD＝22m．
（2）
解：∵，，
当x＝10时，，
∴点F（10，）
∴雕塑EF的高为米．
【点睛】本题考查了二次函数的应用，解题的关键是：（1）利用二次函数图象上点的坐标特征，求出点D的坐标；（2）利用二次函数图象上点的坐标特征，求出抛物线上横坐标为10的点的坐标．
15．（2022·全国·九年级专题练习）如图，在喷水池的中心A处竖直安装一个水管AB．水管的顶端安有一个喷水管、使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C．高度为3m．水柱落地点D离池中心A处3m．建立适当的平面直角坐标系，解答下列问题．

（1）求水柱所在抛物线的函数解析式；
（2）求水管AB的长．
【答案】（1）y＝﹣（x﹣1）2+3（0≤x≤3）；（2）2.25m
【分析】（1）以池中心为原点，竖直安装的水管为y轴，与水管垂直的为x轴建立直角坐标系，设抛物线的解析式为y＝a（x−1）2＋3，将（3，0）代入求得a值；
（2）由题意可得，x＝0时得到的y值即为水管的长．
【详解】解：（1）以池中心为原点，竖直安装的水管为y轴，与水管垂直的为x轴建立直角坐标系．
由于在距池中心的水平距离为1m时达到最高，高度为3m，
则设抛物线的解析式为：y＝a（x﹣1）2+3，
代入（3，0）求得：a＝﹣（x﹣1）2+3．
将a值代入得到抛物线的解析式为：y＝﹣（x﹣1）2+3（0≤x≤3）；
（2）令x＝0，则y＝＝2.25．
故水管AB的长为2.25m．

【点睛】本题考查了二次函数在实际生活中的运用，重点是二次函数解析式的求法，利用顶点式求出解析式是解题关键．
【能力提升】
一、单选题
1．（2022·浙江·桐庐县实验初级中学九年级阶段练习）用20cm长的绳子围成一个矩形，如果这个矩形的一边长为xcm，面积是Scm2，则S与x的函数关系式为（　　）
A．S＝x(20﹣x) B．S＝x(20﹣2x) C．S＝10x﹣x2 D．S＝2x(10﹣x)
【答案】C
【分析】首先表示出矩形的另一边长为（10-x）cm，然后再根据面积=长×宽可得答案．
【详解】解：由题意得：矩形的另一边长为: （10-x）cm，
S＝x（10﹣x）＝．
故选：C．
【点睛】本题主要考查了根据实际问题列二次函数解析式，关键是掌握矩形的面积公式．
2．（2022·全国·九年级专题练习）某景点的“喷水巨龙”口中C处的水流呈抛物线形，该水流喷出的高度y（m）与水平距离x（m）之间的关系如图所示，D为该水流的最高点，DA⊥OB，垂足为A．已知OC＝OB＝8m，OA＝2m，则该水流距水平面的最大高度AD的长度为（　　）．

A．9m B．10m C．11m D．12m
【答案】A
【分析】设抛物线解析式为y＝a（x﹣2）2+k，将点C（0，8）、B（8，0）代入求出a、k的值即可．
【详解】解：根据题意，设抛物线解析式为y＝a（x﹣2）2+k，
将点C（0，8）、B（8，0）代入，得：
，
解得，
∴抛物线解析式为y＝﹣（x﹣2）2+9，
∴当x＝2时，y＝9，
即AD＝9m，
故选：A．
【点睛】本题考查二次函数的实际应用，解题关键是用待定系数法求出函数的解析式．

二、填空题
3．（2022·湖北省咸宁市嘉鱼县城北中学九年级阶段练习）如图用一段长为16m的篱笆围成一个一边靠墙的矩形围栏（墙长9m），则这个围栏的最大面积为________ ．

【答案】32
【分析】设与墙垂直的一边长为xm，然后根据矩形面积列出函数关系式，从而利用二次函数的性质分析其最值．
【详解】解：设与墙垂直的一边长为xm，则与墙平行的一边长为（16-2x）m，
∴矩形围栏的面积为
∵ 墙长9m
∴16-2x≤9  即 x≥
∴当x=4时，矩形有最大面积为，
故答案为：32．
【点睛】本题考查二次函数的应用，准确识图，理解二次函数的性质是解题关键．
4．（2022·浙江·舟山市普陀第二中学九年级阶段练习）如图，人工喷泉有一个竖直的喷水枪，喷水口A距地面，喷出水流的运动路线是抛物线，如果水流的最高点P到喷水枪所在直线的距离为，且到地面的距离为，则水流的落地点C到水枪底部B的距离为__________m．

【答案】##
【分析】建立以所在直线为轴、所在直线为轴的直角坐标系，根据顶点设其解析式为，把代入求得的值，据此可得其函数解析式，再求得时的值可得答案．
【详解】解：如图，以所在直线为轴、所在直线为轴建立直角坐标系，

由题意知，抛物线的顶点的坐标为、点，
设抛物线的解析式为，
将点代入，得：，
解得：，
则抛物线的解析式为：，
当时，有，
解得：（舍或，
m，
答：水流的落地点到水枪底部的距离为．
故答案为：．
【点睛】本题主要考查二次函数的应用，解题的关键是结合题意建立合适的平面直角坐标系，将实际问题转化为二次函数问题求解．
5．（2022·四川广安·九年级专题练习）公园要建造一个如图1的圆形喷水池，在水池中央垂直于水面安装一个花形柱子OA，O恰在水面中心，OA＝0.8米，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，且在过OA的任一平面上抛物线路径如图2所示．为使水流形状较为漂亮，设计成水流在与OA水平距离为1米时，达到距水面最大高度1.44米（不计其他因素）．则水池的半径至少要 _____米，才能使喷出的水流不致落到池外．

【答案】2.5
【分析】根据题意求得二次函数图象的顶点坐标，设顶点式，待定系数法求解析式，然后根据令y=0，即可求解．
【详解】根据题意可得抛物线的顶点坐标为，且图象过点，
，
，
，则，
当时，，即，
解得，（舍去），故水池半径至少为2.5米．
故答案为：2.5．
【点睛】本题考查了二次函数的实际应用，根据题意求得解析式是解题的关键．
6．（2022·吉林长春·九年级期末）如图，某广场有一喷水池，水从地面喷出，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y＝﹣2x2+8x（单位：米）的一部分，则水喷出的最大高度是________米．

【答案】8
【分析】水喷出的最大高度就是水在空中划出的抛物线y=-2x2+8x的顶点纵坐标，将y=-2x2+8x写成顶点式即可得出顶点坐标，从而求得答案．
【详解】解：由题意可知，水喷出的最大高度就是水在空中划出的抛物线y=-2x2+8x的顶点纵坐标，
∵y=-2x2+8x
=-2（x2-4x）
=-2（x-2）2+8，
∴顶点坐标为（2，8），
∴水喷出的最大高度是8米．
故答案为：8．
【点睛】本题考查了二次函数在实际问题中的应用，将实际问题与数学模型联系起来是解题的关键．

三、解答题
7．（2022·全国·九年级专题练习）如图，用一段长为30m的篱笆围出一个一边靠墙的矩形菜园，墙长为18m．设矩形的一边长为xm，面积为y．

(1)求y与x的函数关系式，（不必写出自变量x的取值范围）
(2)写出此二次函数的二次项系数、一次项系数和常数项；
(3)写出次函数的图像的对称轴及顶点坐标．
【答案】(1)y=-+15x（0＜x≤18），
(2)二次项系数为，一次项系数为15，常数项为0
(3)对称轴x=15；及顶点坐标(15，)

【分析】（1）求出矩形的另一边长，根据矩形的面积=长×宽，可得出y与x的函数关系式，结合墙的长度可得出自变量的取值范围；
（2）根据（1）中的函数关系式可直接写出二次项系数、一次项系数和常数项；
（3）配成顶点式，即可求解．
（1）
解：依题意得，矩形的另一边长为，
则y=x=，
由图形可得，自变量x的取值范围是0＜x≤18，
∴y与x的函数关系式为y=（0＜x≤18）；
（2）
解：∵y与x的函数关系式为y=，
∴二次项系数为，一次项系数为15，常数项为0；
（3）
解：y=，
∴对称轴：直线x=15；及顶点坐标(15，) ．
【点睛】本题考查了二次函数的应用，解答本题的关键是表示出矩形的另一边长，得出y与x的函数关系式．
8．（2022·江苏·九年级专题练习）如图，墙壁EF长24米，需要借助墙壁围成一个矩形花园ABCD，现有围栏40米，设AB长x米．

(1)BC的长为 　 　米（用含x的式子表示）；
(2)求这个花园的面积最大值．
【答案】(1)（40-2x）
(2)200平方米

【分析】（1）由AB+BC+CD=40米，AB=CD=x米可得答案；
（2）根据矩形的面积公式得出y=x（40-2x）=-2x2+40x=-2（x-10）2+200，再利用二次函数的性质求解即可．
（1）
解：由题意知AB+BC+CD=40米，AB=CD=x米，
所以BC的长为（40-2x）米，
故答案为：（40-2x）；
（2）
解：设这个花园的面积为y 平方米，由题意得：
y=x（40-2x）
=-2x2+40x
=-2（x-10）2+200，
∵-2＜0，
∴当x=10时，y取得最大值，最大值为200，
答：这个花园的面积最大值为200平方米．
【点睛】本题考查二次函数的应用，关键是根据等量关系写出函数解析式．
9．（2022·全国·九年级课时练习）根据下面的条件列出函数解析式，并判断列出的函数是否为二次函数：
(1)如果两个数中，一个比另一个大5，那么，这两个数的乘积p是较大的数m的函数；
(2)一个半径为10cm的圆上，挖掉4个大小相同的正方形孔，剩余的面积S（cm2）是方孔边长x（cm）的函数；
(3)有一块长为60m、宽为40m的矩形绿地，计划在它的四周相同的宽度内种植阔叶草，中间种郁金香，那么郁金香的种植面积S（cm2）是草坪宽度a（m）的函数．
【答案】(1)p= m2﹣5m，是二次函数
(2)=100π﹣4x2，是二次函数
(3)=4a2﹣200a+2400；是二次函数

【分析】（1）较大的数是m，则较小的数是（m-5），这两个数的乘积为m（m﹣5），根据题意得出p与m的函数关系，由二次函数的定义得出此函数是二次函数；
（2）方孔边长x（cm），则方孔面积为x2cm2；4个大小相同的正方形孔的面积为4x2cm，半径为10cm的圆的面积为100πcm2，则剩余部分的面积为(100π﹣4x2)cm2，根据题意得出列出函数关系式，根据函数定义可知此函数是二次函数；
（3）草坪宽度a（m）则种植郁金香部分矩形的长和宽为（60﹣2a）米与（40﹣2a）米，根据矩形的面积公式列出S与a的函数关系式，根据函数定义得出此函数是二次函数．
(1)
解：这两个数的乘积p与较大的数m的函数关系为：p=m（m﹣5）=m2﹣5m，是二次函数；
(2)
解：剩余的面积S（cm2）与方孔边长x（cm）的函数关系为：S=100π﹣4x2，是二次函数；
(3)
解：郁金香的种植面积S（cm2）与草坪宽度a（m）的函数关系为：S=（60﹣2a）（40﹣2a）=4a2﹣200a+2400，是二次函数；
【点睛】本题主要考查了二次函数的定义，熟练的掌握二次函数的定义并根据题意找出等量关系列出函数表达式是解题的关键．
10．（2022·全国·九年级课时练习）如图，用一根长60厘米的铁丝制作一个“日”字型框架ABCD，铁丝恰好全部用完．

(1)若所围成矩形框架ABCD的面积为144平方厘米，则AB的长为多少厘米？
(2)矩形框架ABCD面积最大值为______平方厘米．
【答案】(1)AB的长为8厘米或12厘米．
(2)150

【分析】（1）设AB的长为x厘米，则有厘米，然后根据题意可得方程，进而求解即可；
（2）由（1）可设矩形框架ABCD的面积为S，则有，然后根据二次函数的性质可进行求解．
（1）
解：设AB的长为x厘米，则有厘米，由题意得：
，
整理得：，
解得：，
∵，
∴，
∴都符合题意，
答：AB的长为8厘米或12厘米．
（2）
解：由（1）可设矩形框架ABCD的面积为S平方厘米，则有：
，
∵，且，
∴当时，S有最大值，即为；
故答案为：150．
【点睛】本题主要考查一元二次方程及二次函数的应用，解题的关键是找准题干中的等量关系．
11．（2022·全国·九年级专题练习）如图，Rt△ABC中，∠C＝90°，AC＝6，BC＝8，动点P、Q分别从A、C两点同时出发，P点沿边AC向C以每秒3个单位长度的速度运动，Q点沿边BC向B以每秒4个单位长度的速度运动，当P、Q到达终点C、B时，运动停止，设运动时间为t（s）．
（1）①当运动停止时，t的值为 ；
②设P、C之间的距离为y，则y与t满足 关系（填“正比例函数”、“一次函数”或“二次函数”）；
（2）设△PCQ的面积为S．
①求S的表达式（用含t的式子表示）；
②求当t为何值时，S取得最大值，这个最大值是多少？

【答案】（1）①2；②一次函数；（2）①；②，面积最大为
【分析】（1）①根据运动速度，以及、的长度，即可求解；②求得与的关系式，即可求解；
（2）①求得线段、的长度，即可求得S的表达式；②根据表达式可得S与t为二次函数的关系，根据二次函数的性质即可求解．
【详解】解：（1）①运动停止时，分别到达终点点和B点，

故答案为
②由题意可得：，，即，∴y与t满足一次函数的关系
故答案为一次函数
（2）①由题意可得：，

△PCQ的面积
故答案为：
②由二次函数的性质可得：，开口向下，对称轴为
∴当时，取得最大值，最大值为
【点睛】此题考查了函数与几何的综合应用，涉及了正比例函数的性质，二次函数的性质，解题的关键是掌握二次函数的有关性质，理解题意，找到题中的等量关系．
12．（2022·全国·九年级专题练习）如图，在△ABC中，∠B=90°，AB=12cm，BC=24cm，动点P从点A开始沿边AB向点B以2cm/s的速度移动，动点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果P，Q两点分别从A，B两点同时出发，设运动时间为ts，

（1）BP=_________cm；BQ=_________cm；
（2）t为何值时△PBQ的面积为32cm2?
（3）t为何值时△PBQ的面积最大？最大面积是多少？
【答案】（1）12-2t，4t；（2）当t=2秒或4秒时，△PBQ的面积是32cm2；（3）当t为3时△PBQ的面积最大，最大面积是36cm2．
【分析】（1）根据题意得出即可；
（2）根据题意和三角形的面积列出方程，求出方程的解即可；
（3）先列出函数解析式，再化成顶点式，最后求出最值即可．
【详解】解：（1）根据题意得：AP=2tcm，BQ=4tcm，
所以BP=（12-2t）cm，
故答案为：12-2t，4t；
（2）△PBQ的面积S=×BP×BQ
=×（12-2t）×4t
=-4t2+24t=32，
解得：t=2或4，
即当t=2秒或4秒时，△PBQ的面积是32cm2；
（3）由题意得：S=-4t2+24t
=-4（t-3）2+36，
所以当t为3时△PBQ的面积最大，最大面积是36cm2．
【点睛】本题考查了三角形的面积，二次函数的最值等知识点，能求出S与x的函数关系式是解此题的关键．
13．（2022·全国·九年级专题练习）如图（单位：），等腰直角三角形以的速度沿直线l向正方形移动，直到与重合．设时，三角形与正方形重叠部分的面积为．

（1）写出y与x的关系式；
（2）当，3.5时，y分别是多少？
（3）当重叠部分的面积是正方形面积的一半时，三角形移动了多长时间？
【答案】（1）；（2）8，24.5；（3）当重叠部分的面积是正方形的一半时，三角形移动了5s．
【分析】（1）根据题意可知，三角形与正方形重合部分是个等腰直角三角形，且直角边都是2x，据此可得出y、x的函数关系式；
（2）可将x的值，代入（1）的函数关系式中，即可求得y的值；
（3）将正方形的面积的一半代入（1）的函数关系式中，即可求得x的值．（其实此时AB与DC重合，也就是说等腰三角形运动的距离正好是正方形的边长10m，因此x=5）
【详解】解：（1）因为三角形与正方形重合部分是个等腰直角三角形，且直角边都是2x，
所以y=×2x×2x=2x2；
（2）在y=2x2中，
当x=2时，y=8；
当x=3.5时，y=24.5；
（3）在y=2x2中，
因为当y=50时，2x2=50，
所以x2=25，
解得x=5s（负值舍去）．
即当重叠部分的面积是正方形的一半时，三角形移动了5s．
【点睛】本题考查了正方形的性质、等腰直角三角形的判定与性质、平移的性质以及函数关系式等知识；本题综合性强，熟练掌握正方形的性质和等腰直角三角形的性质是解题的关键，求出y与x之间的函数解析式是解题的关键．
14．（2022·山东·乳山市乳山寨镇中心学校九年级阶段练习）如图所示，某建筑工地准备利用一面旧墙建一个矩形储料场，新建墙的总长为30米．

(1)当矩形ABCD的长和宽分别为多少时，矩形的面积最大？
(2)若要使矩形的面积为72平方米，长和宽应取多少米？
【答案】(1)当长为15米、宽为米时，矩形面积最大，最大是平方米；
(2)当长为24米、宽为3米或长为12米、宽为6米时，矩形面积为72平方米．

【分析】（1）设长BC的长为x米，根据矩形的面积列出函数解析式，根据函数的性质求最值即可；
（2）令y=72，解方程即可求解．
（1）
解：设长BC的长为x米，矩形ABCD的面积为y平方米，
则，
∵-＜0，
∴当x=15时，y最大值，最大值为，
，
∴当长为15米、宽为米时，矩形面积最大，最大是平方米；
（2）
解：令y=72，则，
整理得，
解得：=24，=6，
答：当长为24米、宽为3米或长为12米、宽为6米时，矩形面积为72平方米．
【点睛】本题主要考查二次函数和一元二次方程的应用，根据矩形的面积公式得出函数解析式和一元二次方程是解题关键．
15．（2022·浙江·九年级单元测试）如图，正方形的顶点在边长为的正方形的边上，若，正方形的面积为．

(1)求出与之间的函数关系式；
(2)正方形有没有最小面积？若有，试确定点位置；若没有，说明理由．
【答案】(1)
(2)有最小面积，此时为中点

【分析】（1）先根据正方形的性质、三角形全等的判定证出，再根据全等三角形的性质可得，然后在中，利用勾股定理可得，最后利用正方形的面积公式即可得；
（2）利用二次函数的性质求解即可得．
（1）
解：四边形是正方形，
，，
，
四边形是正方形，
，
，
，
在和中，，
，
，
正方形的边长为，，正方形的面积为，
，，，
在中，，
．
（2）
解：由（1）可知，，
由二次函数的性质可知，在内，当时，取得最小值，
所以正方形有最小面积，此时点为中点．
【点睛】本题考查了正方形的性质、三角形全等的判定与性质、二次函数的应用，熟练掌握正方形和二次函数的性质是解题关键．
16．（2022·辽宁·大连市第七十六中学九年级阶段练习）如图，在边长为的正方形中，点沿边从点开始沿向点以的速度移动；同时，点沿边从点开始向点以的速度移动．设点出发s时．

(1)求的面积为与的函数关系式，并直接写出取值范围；
(2)若的面积为正方形面积的时，求的值．
【答案】(1)
(2)或

【分析】（1）分三种情况讨论，即在上，分别列出根据三角形的面积列出函数关系式即可求解；
（2）根据题意求得正方形面积的，结合（1）的解析式，令，解方程即可求解．
（1）
解：∵正方形的边长为，点以的速度移动，点以的速度移动，点出发s
∵，，
∴的运动时间为，
①当时，点在上，依题意，，

∴，
②当点在上时，时，如图，

，
③当点在上时，，如图，

∴，
∴，
综上所述，，
（2）
∵正方形的面积为，
当的面积为正方形面积的时，即，
①当时，，
解得：，
∵，
∴不存在，
②当时，，
解得：，
③当时，，
解得：（舍去），
综上所述，当或时，的面积为正方形面积的．
【点睛】本题考查了一次函数、二次函数与动点问题，根据题意分类讨论列出函数关系式是解题的关键．