




人教版九年级上册21.2.4 一元二次方程的根与系数的关系获奖ppt课件
展开1.探索一元二次方程的根与系数的关系.(重点)2.不解方程利用一元二次方程的根与系数的关系解决问题.(难点)
1.一元二次方程的一般形式是什么?
2、一元二次方程的求根公式?
( )
一元二次方程的一般形式是:
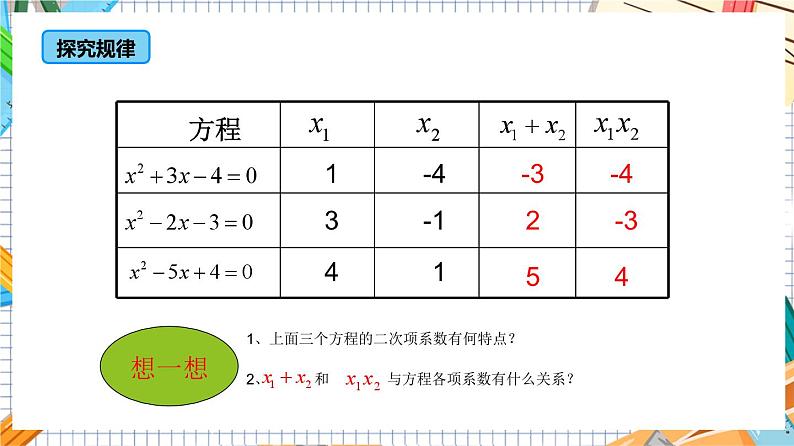
1、上面三个方程的二次项系数有何特点?
利用公式法求方程的两根:
说明它也有这样的结论。
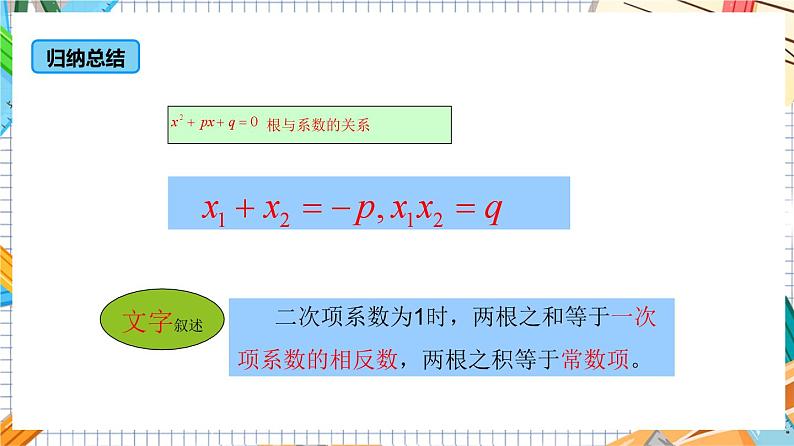
二次项系数为1时,两根之和等于一次 项系数的相反数,两根之积等于常数项。
猜一猜:通过上表猜想,如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么,你可以发现什么结论?
一元二次方程的根与系数的关系 (韦达定理)
如果 ax2+bx+c=0(a≠0)的两个根为x1、 x2,那么
满足上述关系的前提条件
例1 利用根与系数的关系,求下列方程的两根之和、两根之积.(1)x2 – 6x – 15 = 0;
解:这里 a = 1 , b = – 6 , c = – 15 . Δ = b2 - 4ac =( – 6 )2 – 4 × 1 ×(– 15 ) = 96 > 0. ∴方程有两个实数根. 设方程的两个实数根是 x1, x2,那么 x1 + x2 = – ( – 6 ) =6, x1 x2 = – 15 .
(2)3x2 +7x-9 = 0;
解:这里 a = 3 , b = 7, c = -9.
Δ=b2 − 4ac = 72 – 4 × 3 × (− 9) = 157 > 0,
设方程的两个实数根是 x1,x2,那么
(3) 5x – 1 = 4x2 .
解:方程可化为 4x2 – 5x +1 =0,这里 a =4, b = – 5,c = 1. Δ = b2 − 4ac =( – 5 )2 – 4 × 4 ×1 = 9 > 0.∴方程有两个实数根.设方程的两个实数根是 x1,x2,那么 x1 + x2 = , x1 x2 = .
在运用韦达定理求两根之和、两根之积时,先把方程化为一般式,再分别代入a、b、c的值即可 .
例2 已知方程5x2+kx−6=0的一个根是2,求它的另一个根及k的值.
解:设方程的两个根分别是x1、x2,其中x1=2 . 所以 x1 · x2=2x2= 即 x2= 由于x1+x2=2+ = 得 k=−7.答:方程的另一个根是 ,k=−7.
变式:已知方程3x2−18x+m=0的一个根是1,求它的另一个根及m的值.
解:设方程的两个根分别是x1、x2,其中x1=1. 所以 x1 + x2=1+x2=6, 即 x2=5 . 由于x1·x2=1×5= 得 m=15.答:方程的另一个根是5,m=15.
例3 不解方程,求方程2x2+3x-1=0的两根的平方和、倒数和.
解:根据根与系数的关系可知:
首先要验证判别式△≥0,才能开始两根的运算!
设x1,x2为方程x2−4x+1=0的两个根,则: (1) x1+x2= , (2)x1·x2= , (3) , (4) .
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
例4 设x1,x2是方程 x2 -2(k - 1)x + k2 =0 的两个实数根,且x12 +x22 =4,求k的值.
解:由方程有两个实数根,得Δ= 4(k − 1)2− 4k2 ≥ 0 即 −8k + 4 ≥ 0. 由根与系数的关系得 x1 + x2 = 2(k -1) , x1 x2 =k 2. ∴ x12 + x22 = (x1 + x2)2 - 2x1x2 = 4(k -1)2 -2k2 = 2k2 -8k + 4. 由 x12 + x22 = 4,得 2k2 - 8k + 4 = 4, 解得 k1= 0, k2 = 4 . 经检验, k2 = 4 不合题意,舍去.所以k=0.
根据一元二次方程两实数根满足的条件,求待定字母的值时,务必要注意方程有两实数根的条件,即所求的字母应该满足△≥0.
2.【广东中考】已知x1、x2是一元二次方程x2-2x=0的两个实数根,下列结论错误的是( )A.x1≠x2B.x-2x1=0C.x1+x2=2D.x1·x2=2
3.【湖北随州中考】已知关于x的一元二次方程x2-(2k+1)x+k2+1=0有两个不相等的实数根x1、x2.(1)求k的取值范围;(2)若x1+x2=3,求k的值及方程的根.
1.若关于x的方程x2+3x+a=0有一个根为-1,则另一个根为( )A.-2B.2C.4D.-3
7.已知方程 3x2 −19x + m=0的一个根是1,求它的另一 个根及m的值.
解:将x = 1代入方程中 3−19 + m = 0. 解得 m = 16, 设另一个根为x1,则: 1 × x1 = ∴x1 =
8.已知x1, x2是方程2x2+2kx+k-1=0的两个根,且(x1+1)(x2+1)=4; (1)求k的值; (2)求(x1−x2)2的值.
解:(1)根据根与系数的关系得 所以(x1+1)(x2+1)=x1x2+(x1+x2)+1= 解得 k=−7.
(2)因为k=−7,所以 则:
9.设x1,x2是方程3x2 + 4x – 3 = 0的两个根.利用根与系数之间的关系,求下列各式的值. (1) (x1 + 1)(x2 + 1); (2)
解:根据根与系数的关系得: (1)(x1 + 1)(x2 + 1) = x1 x2 + (x1 + x2 )+ 1= (2)
10.【易错题】关于x的一元二次方程x2+2mx+m2+m=0的两个实数根的平方和为12,则m的值为( )A.m=-2B.m=3C.m=3或m=-2D.m=-3或m=211.已知m、n是关于x的一元二次方程x2-2tx+t2-2t+4=0的两实数根,则(m+2) (n+2)的最小值是( )A.7B.11C.12D.16
13. 当k为何值时,方程2x2−kx+1=0的两根差为1.
解:设方程两根分别为x1,x2(x1>x2),则x1−x2=1
∵ (x1-x2)2=(x1+x2)2-4x1x2=1
14.已知关于x的一元二次方程mx2−2mx+m −2=0. (1)若方程有实数根,求实数m的取值范围. (2)若方程两根x1,x2满足|x1-x2|= 1, 求m的值.
解:(1)方程有实数根
∵m≠0,∴m的取值范围为m>0.
(2)∵方程有实数根x1,x2,
∵ (x1-x2)2=(x1+x2)2-4x1x2=1,
经检验m=8是方程的解.
15.已知关于x的一元二次方程x2-2x+k=0.(1)若方程有实数根,求k的取值范围;(2)如果k是满足(1)的最大的整数,且方程x2-2x+k=0的一个根的相反数是一元二次方程(m-1)x2-3mx-7=0的一个根,求m的值及这个方程的另一个根.解:(1)∵关于x的一元二次方程x2-2x+k=0有实数根,∴Δ=4-4k≥0,解得k≤1,∴k的取值范围是k≤1. (2)∵k≤1,∴k的最大整数值是1,则关于x的方程x2-2x+k=0是x2-2x+1=0,解得x1=x2=1.∵方程x2-2x+k=0的一个根的相反数是一元二次方程(m-1)x2-3mx-7=0的一个根,∴当x=-1时,(m-1)+3m-7=0,解得m=2.这个方程的另一个根为-7÷(-1)=7.
16.如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如:一元二次方程x2-6x+8=0的两个根是2和4,则方程x2-6x+8=0就是“倍根方程”.(1)若一元二次方程x2-3x+c=0是“倍根方程”,求c的值;(2)若关于x的一元二次方程ax2+bx+c=0(a≠0)是“倍根方程”,则a、b、c之间有何关系?(3)若(x-2)(mx-n)=0(m≠0)是“倍根方程”,求代数式4m2-5mn+n2的值.
根与系数的关系(韦达定理)
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
初中数学人教版九年级上册21.2.4 一元二次方程的根与系数的关系教案配套ppt课件: 这是一份初中数学人教版九年级上册21.2.4 一元二次方程的根与系数的关系教案配套ppt课件,共25页。PPT课件主要包含了学习目标,复习引入,x1+x2-3,x1·x2-4,x1+x25,x1·x26,猜一猜,x2+px+q0,证一证,b2-4ac≥0等内容,欢迎下载使用。
2021学年第二十一章 一元二次方程21.2 解一元二次方程21.2.4 一元二次方程的根与系数的关系示范课ppt课件: 这是一份2021学年第二十一章 一元二次方程21.2 解一元二次方程21.2.4 一元二次方程的根与系数的关系示范课ppt课件,共24页。PPT课件主要包含了学习目标,导入新课,复习引入,讲授新课,x1+x2-3,x1·x2-4,x1+x25,x1·x26,猜一猜,x2+px+q0等内容,欢迎下载使用。
2020-2021学年21.2.4 一元二次方程的根与系数的关系图文ppt课件: 这是一份2020-2021学年21.2.4 一元二次方程的根与系数的关系图文ppt课件,共9页。PPT课件主要包含了-ba等内容,欢迎下载使用。













