






初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数获奖ppt课件
展开1.理解掌握二次函数的概念和一般形式.(重点)2.会利用二次函数的概念解决问题.3.能根据实际问题列二次函数表达式.(难点)
如图,从喷头喷出的水珠,在空中走过一条曲线后落到池中央,在这条曲线的各个位置上,水珠的竖直高度h与它距离喷头的水平距离x之间有什么关系?
上面问题中变量之间的关系可以用哪一种函数来表示?这种函数与以前学习的函数、方程有哪些联系?
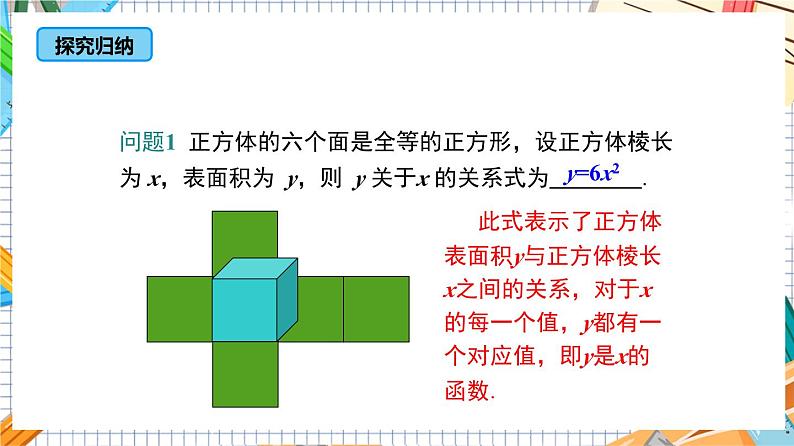
问题1 正方体的六个面是全等的正方形,设正方体棱长为 x,表面积为 y,则 y 关于x 的关系式为 .
此式表示了正方体表面积y与正方体棱长x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
问题2 n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
分析:每个球队n要与其他 个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛是同一场比赛,所以比赛的场次数为 .
此式表示了比赛的场次数m与球队数n之间的关系,对于n的每一个值,m都有一个对应值,即m是n的函数.
问题3 某种产品现在的年产量是20 t,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系怎样表示?
分析:这种产品的原产量是20 t,一年后的产量是 t,再经过一年后的产量是 t,即两年后的产量y=________.
此式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
问题1-3中函数关系式有什么共同点?
函数都是用自变量的二次整式表示的
y=20x2+40x+20
一般地,形如y=ax²+bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数.其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
(1)等号左边是变量y,右边是关于自变量x的整式;(2)a,b,c为常数,且a≠ 0;(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项.
例1 下列函数中哪些是二次函数?为什么?(x是自变量)① y=ax2+bx+c ② y=3−2x² ③y=x2 ④ ⑤y=x²+x³+25 ⑥ y=(x+3)²−x²
不一定是,缺少a≠0的条件.
不是,等式右边是分式.
不是,x的最高次数是3.
1 下列函数中是二次函数的有 。
二次函数:y=ax²+bx+c(a,b,c为常数,a≠0)
是,二次项系数:−5.
是,二次项系数:3,一次项系数:−21,常数项:30.
判断一个函数是不是二次函数,先看原函数和整理化简后的形式再作判断.除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有一些特殊形式如y=ax2,y=ax2+bx,y=ax2+c等.
例2 关于x的函数 是二次函数, 求m的值.
解: 由二次函数的定义得m2-m=2,m+1≠0
注意 二次函数的二次项系数不能为零.
解得 m=2.因此当m=2时,函数为二次函数.
本题易忽略二次项系数a≠0这一限制条件,从而得出m=-1的错误答案,需要引起同学们的重视.
问题 矩形绿地的长为x m,面积为y m2.
(1)若该矩形绿地的长为宽的2倍,则宽为____m, y 与x之间的关系式为__________.
(2)若该矩形绿地的长比宽多6 m,则宽为______m, y 与x之间的关系式为___________.
想一想 自变量的取值范围是___________.
例3 一农民用40m长的篱笆围成一个一边靠墙的长方形菜园,和墙垂直的一边长为xm,菜园的面积为ym2,求y与x之间的函数关系式,并说出自变量的取值范围。当x=12m时,计算菜园的面积。
(40-2x )m
y=x(40-2x)
即 y=-2x2+40x
当x=12m时,菜园的面积为
y =-2x2+40x=-2×122+40×12 =192(m2)
方法点拨:确定实际问题中的二次函数关系式时,常常用到生活中的经验及数学公式(例长方形和圆的面积、周长公式)等。
例4 某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式.
∴y=[6+2(x−1)][95−5(x−1)],
解:∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天产量减少5件,
∴第x档次,提高了(x-1)档,利润增加了2(x-1)元,产量减少了5(x-1)件.
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10).
1.函数 y=(m−n)x2+ mx+n 是二次函数的条件是( )
A.m,n是常数,且m≠0 B.m,n是常数,且n≠0C.m,n是常数,且m≠n D.m,n为任何实数
2.已知函数 y=3x2m−1−5. ① 当 m= 时,y 是关于 x 的一次函数; ② 当 m= 时,y 是关于 x 的二次函数 .
3.已知函数 y=(m²﹣m)x²+(m﹣1)x+m+1.(1)若这个函数是一次函数,求m的值;(2)若这个函数是二次函数,则m的值应怎样?解:(1)根据一次函数的定义,得m2﹣m=0, 解得m=0或m=1,又∵m﹣1≠0即m≠1; ∴当m=0时,这个函数是一次函数; (2)根据二次函数的定义, 得:m2﹣m≠0,解得m1≠0,m2≠1; ∴当m1≠0,m2≠1时,这个函数是二次函数.
4.某工厂生产的某种产品按质量分为 10 个档次,第1档次(最低档次)的产品一天能生产 95 件,每件利润 6 元.每提高一个档次,每件利润增加 2 元,但一天产量减少 5 件.(1)若生产第 x 档次的产品一天的总利润为y元(其中 x 为正整数,且1≤x≤10),求出 y 关于 x 的函数关系式;
解:因为第1档次的产品一天能生产 95 件,每件利润 6 元,每提高一个档次,每件利润增加 2 元,但一天产量减少 5 件,所以第 x 档次,提高了(x−1)档,利润增加了 2(x−1)元.所以 y=[6+2(x−1)][95−5(x−1)],即 y=−10x2+180x+400(其中 x 是正整数,且1≤x≤10).
(2)若生产第 x 档次的产品一天的总利润为 1 120 元,求该产品的质量档次.
解:由题意可得 −10x2+180x+400=1120,整理得 x2−18x+72=0,解得 x1=6,x2=12(舍去).所以该产品的质量档次为第6档.
某工厂生产的某种产品按质量分为 10 个档次,第1档次(最低档次)的产品一天能生产 95 件,每件利润 6 元.每提高一个档次,每件利润增加 2 元,但一天产量减少 5 件.
下列函数中,哪些是二次函数?
(1) y=3(x-1)²+1
(3) s=3-2t²
(5) y=(x+3)²-x²
(6) v =10πr²
(7) y=x²+x³+25
(8) y =2²+2x
整理后,自变量的最高次数是1
解:根据二次函数的定义,得
是二次函数,求常数a的值.
3.①已知圆的面积y(cm2)与圆的半径x(cm),写出y与x之间的函数关系式;②王先生存入银行2万元,先存一个一年定期,一年后银行将本息自动转存为又一个一年定期,设一年定期的存款年利率为x,两年后王先生共得本息和y万元,写出y与x之间的函数关系式;③一个圆柱的高等于底面半径,写出它的表面积S与半径r之间的关系式.
说一说以上二次函数解析式的各项系数。
4.矩形的周长为16cm,它的一边长为x(cm),面积为y(cm2).(1)写出y与x之间的函数解析式及自变量x的取值范围;(2)当x=3时,求矩形的面积.
解:(1)y=(8−x)x=−x2+8x (0<x<8);
(2)当x=3时,y=−32+8×3=15 (cm2) .
5.如图,矩形绿地的长、宽各增加 x m,写出扩充后的绿地的面积 y 与 x 的关系式.
解:由图可得,扩充后的绿地的面积y(m2)与 x(m)之间的函数关系式是y=(30+x)(20+x)=x2+50x+600,即 y=x2+50x+600.
y=ax2+bx+c(a ≠0,a,b,c是常数)
右边是整式;自变量的最高次数是2;二次项系数a ≠0.
y=ax2;y=ax2+bx;y=ax2+c(a ≠0,a,b,c是常数).
人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数教学ppt课件: 这是一份人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数教学ppt课件,共19页。PPT课件主要包含了唯一确定,自变量,二次函数,变量之间的关系,一次函数,1+x,二次项,一次项,常数项,二次项系数等内容,欢迎下载使用。
初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数说课ppt课件: 这是一份初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数说课ppt课件,共22页。PPT课件主要包含了什么是函数,探究归纳,y6x2,n−1,1+x2,想一想,二次函数的定义,温馨提示,归纳总结,y6x+9等内容,欢迎下载使用。
初中数学人教版九年级上册22.1.1 二次函数获奖ppt课件: 这是一份初中数学人教版九年级上册22.1.1 二次函数获奖ppt课件,文件包含人教版数学九年级上册2211《二次函数》课件pptx、人教版数学九年级上册2211《二次函数》教案docx、人教版数学九年级上册2211《二次函数》课时练docx等3份课件配套教学资源,其中PPT共26页, 欢迎下载使用。













