人教版数学九年级上册22.1.3 《二次函数y=a(x-h)%U00B2的图象和性质》（第2课时）课件）

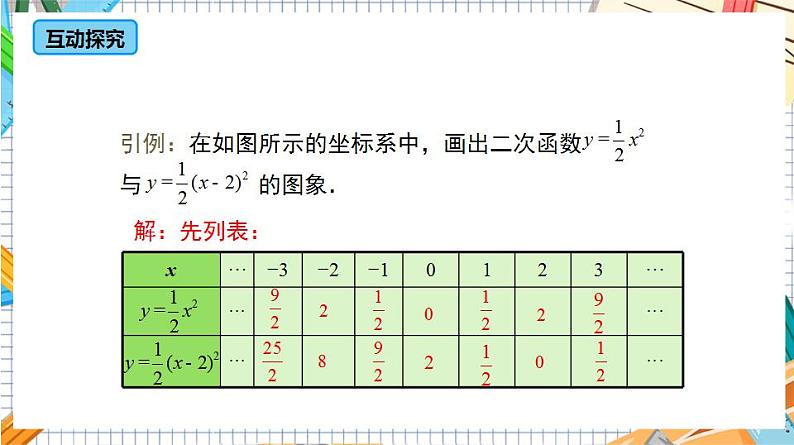
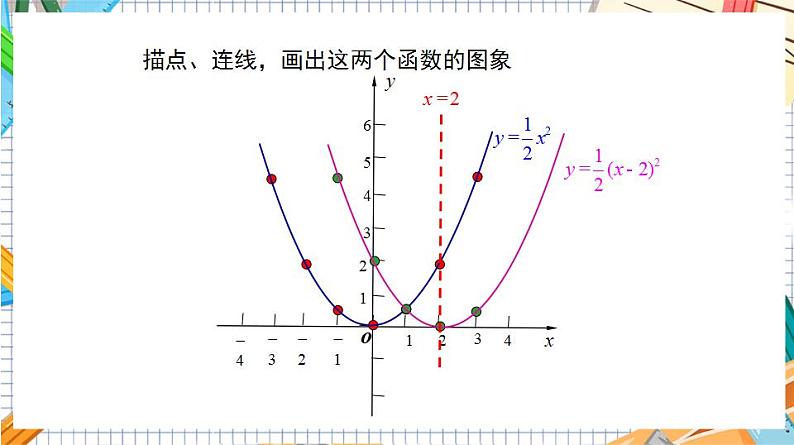
22.1.3 二次函数y=a(x-h)²的图象和性质（第2课时）第22章 二次函数人教版数学九年级上册目录情境引入学习目标1.会画二次函数y=a(x−h)2的图象.（重点）2.掌握二次函数y=a(x−h)2的性质.（难点）3.比较函数y=ax2 与 y=a(x−h)2的联系.向上向下y轴（直线x=0）y轴（直线x=0）（0，c）（0，c）当x<0时，y随x增大而减小；当x>0时，y随x增大而增大.当x<0时，y随x增大而增大；当x>0时，y随x增大而减小.x=0时，y最小值=cx=0时，y最大值=c问题1 说说二次函数y=ax2+c(a≠0)的图象的特征.复习回顾问题2 二次函数 y=ax2+k(a≠0)与 y=ax2(a≠0)的图象有何关系？答：二次函数y=ax2+k(a ≠ 0)的图象可以由y=ax2(a ≠ 0)的图象平移得到： 当k > 0 时，向上平移k个单位长度得到. 当k < 0 时，向下平移- k个单位长度得到.互动探究解：先列表：描点、连线，画出这两个函数的图象向上向上y轴x =2(0,0)(2,0)根据所画图象，填写下表：试一试：画出二次函数 的图象，并考虑它们的开口方向、对称轴和顶点．−2−4.5−200−2−2−4.5Oxy−8−8向下直线x=-1( −1 , 0 )直线x=0直线x=1向下向下( 0 , 0 )( 1, 0)二次函数 y=a(x-h)2(a≠0)的性质知识要点(1)完成下表；(2)在如图的坐标系中描点，画出该二次函数的图象．﹣10123202解：描点，画出该二次函数图象如下：典例精析（3）写出该二次函数的图象的对称轴和顶点坐标；（4）当x取何值时，y随x的增大而增大；（3）对称轴为直线x=1.顶点坐标为(1,0).（4）当x＞1时，y随x的增大而增大.（5）若3≤x≤5，求y的取值范围；想一想：若−1≤x≤5，求y的取值范围；（5）∵当x＞1时，y随x的增大而增大，当x=3时，y=2;当x=5时，y=8,∴当3≤x≤5时，y的取值范围为2≤y≤8.∵当−1≤x≤5时，y的最小值为0，∴当−1≤x≤5时，y的取值范围是0≤y≤8.（6）若抛物线上有两点A(x1，y1)，B(x2，y2)，如果x1＜x2＜1，试比较y1与y2的大小．∵m＞1，∴1＜m＜m+1，变式：若点A(m，y1)，B(m+1，y2)在抛物线的图象上，且m＞1，试比较y1，y2的大小，并说明理由．（6）∵当x＜1时，y随x的增大而减小，∴当x1＜x2＜1时，y1＞y2.∵当x＞1时，y随x的增大而增大，∴y1＜y2.1.已知二次函数y=-(x+h)2,当x<-3时，y随x的增大而增大，当x>-3时，y随x的增大而减小，当x=0时，y的值是（ ） A.-1 B.-9 C.1 D.9 B 练一练向右平移1个单位想一想 抛物线 ， 与抛物线 有什么关系？ 向左平移1个单位知识要点二次函数 y=a（x-h)2的图象与y=ax2 的图象的关系可以看作互相平移得到.左右平移规律： 括号内左加右减；括号外不变.y=a(x-h)2当向左平移 ︱h︱ 时y=a(x+h)2当向右平移 ︱h︱ 时y=ax2如何平移：向左平移1个单位向右平移1个单位左：+ 右:-例2 抛物线y＝ax2向右平移3个单位后经过点(-1，4)，求a的值和平移后的函数关系式．解：二次函数y＝ax2的图象向右平移3个单位后的二次函数关系式可表示为y＝a(x−3)2，把x＝−1，y＝4代入，得4＝a(−1−3)2， ，∴平移后二次函数关系式为y＝ (x−3)2.方法总结：根据抛物线左右平移的规律，向右平移3个单位后，a不变，括号内应“减去3”；若向左平移3个单位，括号内应“加上3”，即“左加右减”．2. 将二次函数y＝－2x2的图象平移后，可得到二次函数y＝－2(x＋1)2的图象，平移的方法是(　　)A．向上平移1个单位　　B．向下平移1个单位 C．向左平移1个单位　　D．向右平移1个单位解析 抛物线y＝－2x2的顶点坐标是(0，0)，抛物线y＝－2(x＋1)2的顶点坐标是(－1，0)．则由二次函数y＝－2x2的图象向左平移1个单位即可得到二次函数y＝－2(x＋1)2的图象．C练一练 已知二次函数y=﹣（x﹣h）2（h为常数），当自变量x的值满足2≤x≤5时，与其对应的函数值y的最大值为﹣1，则h的值为（　 ）A．3或6 B．1或6 C．1或3 D．4或6B　中考链接1.抛物线y＝－5(x－2)2的顶点坐标是(　　) A．(－2，0) B．(2，0) C．(0，－2) D．(0，2)B当堂练习2. 在下列二次函数中，其图象的对称轴为直线x＝－2的是(　　) A．y＝(x＋2)2 B．y＝2x2－2 C．y＝－2x2－2 D．y＝2(x－2)2A3.已知抛物线y＝－(x＋1)2上的两点A(x1，y1)，B(x2，y2)，如果x1＜x2＜－1，那么下列结论成立的是(　　)A．y1＜y2＜0 B．0＜y1＜y2C．0＜y2＜y1 D．y2＜y1＜0A4. 二次函数y=-3 (x－5)2的图象可有抛物线y=-3x2沿___轴向___平移___个单位得到，它的开口向___,顶点坐标是_______,对称轴是_________.当x=___时，y有最____值.当x___5时，y随x的增大而增大；当x___5时，y随x的增大而减小.x右下大5（5,0）直线x=55<> 5.指出下列函数图象的开口方向,对称轴和顶点坐标.向上直线x=3( 3, 0 )直线x=2直线x=1向下向上(2, 0 )( 1, 0)6.抛物线y=a(x+h)2的对称轴是直线x=-2,且过点(1,-3).(1)求抛物线的解析式;(2)求抛物线的顶点坐标;(3)当x为何值时,y随x的增大而增大?已知二次函数y＝(x﹣h)2（h为常数），当自变量x的值满足﹣1≤x≤3时，与其对应的函数值y的最小值为4，求h的值.思路分析二次函数图象的对称轴未知(h未知),应分类讨论：分类讨论 h＜−1−1≤h≤3h＞3x=−1时取最小值x=3时取最小值y的最小值为0能力提升解：∵当x＞h时，y随x的增大而增大，当x＜h时，y随x的增大而减小，∴①若h＜−1≤x≤3，x＝−1时，y取得最小值4，可得(−1−h)2＝4，解得h＝﹣3或h＝1（舍）；②若−1≤x≤3＜h，当x＝3时，y取得最小值4，可得：(3−h)2＝4，解得：h＝5或h＝1（舍）；综上，h的值为﹣3或5.③若﹣1＜h＜3时，当x＝h时，y取得最小值为0，不是4，∴此种情况不符合题意，舍去． 复习y=ax2+k探索y=a(x-h)2的图象及性质图象的画法图象的特征描点法平移法开口方向顶点坐标对称轴平移关系直线x=h（h,0）a>0,开口向上a<0,开口向下y=ax2平移规律：括号内：左加右减；括号外不变.课堂小结THANKS“”