人教版数学九年级上册23.1《旋转作图》（第2课时）课件）

这是一份人教版数学九年级上册23.1《旋转作图》（第2课时）课件），共39页。

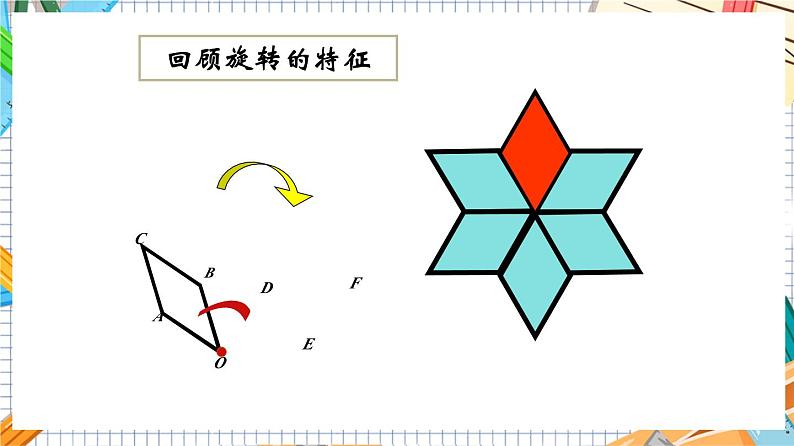
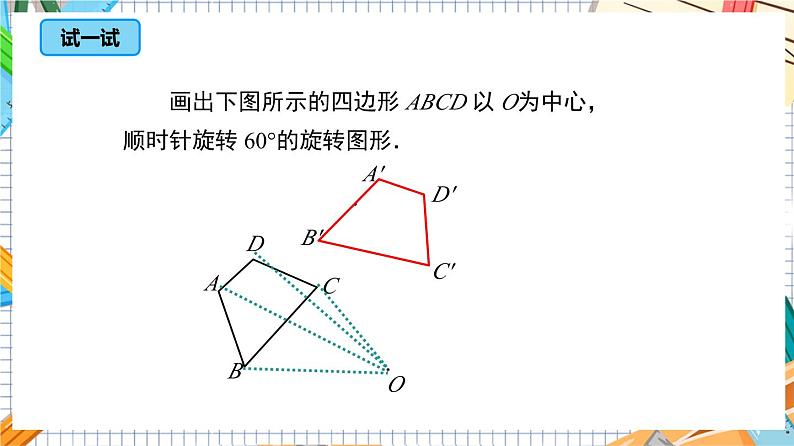
23.1旋转作图（第2课时）第23章 旋转人教版数学九年级上册目录1.复习旋转及旋转图形的概念及基本性质.（重点）2.能够根据旋转的基本性质解决实际问题和进行简 单作图.（难点）OF︵ABCDE回顾旋转的特征 我们上节课已经学习了旋转的概念、旋转的性质，这为我们本节课学习奠定了一定的基础.这节课我们就应用上节课所学的知识展现你的艺术风采.新课引入画一画：如图，画出线段 AB绕点A按顺时针方向旋转60°后的线段．作法：(1)如图，以AB为一边按顺时针方向画∠BAX，使得∠BAX=60°.(2)在射线AX上取点C，使得AC=AB.线段AC为所求．XC　 画出下图所示的四边形 ABCD 以 O为中心，顺时针旋转 60°的旋转图形．试一试B'A'C'D'①相同：都是一种运动；运动前后不改变图形的形状和大小.BACO②不同平移和旋转的异同：归纳总结 例1.如图（1），E是正方形ABCD中CD边上任意一点，以点A为中 心，把△ADE顺时针旋转90°，画出旋转后的图形. 分析：关键是确定△ADE三个顶点的对应点， 即它们旋转后的位置.典例精析知识点解：因为点A是旋转中心，所以它的对应点是它本身.正方形ABCD中，AD=AB，∠DAB=90°，所以旋转后点D与点B重合.设点E的对应点为点E′.因为旋转后的图形与旋转前的图形全等，所以∠ABE′=∠ADE=90°，BE′=DE.因此，在CB的延长线上取点E′，使BE′=DE，则△ABE′为旋转后的图形E ′答：延长CB，以点A为圆心，AE 的长为半径画弧，交CB的延长线于E'，连接AE'，则△ABE'为旋转后的图形.想一想：还有其他方法确定点E的对应点E′吗？E' 简单旋转作图的一般步骤： (1)找出图形的关键点； (2)确定旋转中心，旋转方向和旋转角； (3)将关键点与旋转中心连接起来，然 后按旋转方向分别将它们旋转一个角，得到关键点的对应点； (4)按照原图形的顺序连接这些对应点，所得到的图形就是旋转后的图形．例2.如图23.1-3，△ ABC绕点O旋转，使点A旋转到点D处，画出顺时针旋转后的三角形，并写出简要作法典例精析解题秘方：在旋转作图时，要紧扣以下三点(1)对应点到旋转中心的距离相等；(2)旋转的角度相等；(3)旋转的方向相同.解：作法：(1)连接OA，OB，OC，OD；(2)分别以OB，OC 为边作∠ BOM= ∠ CON= ∠ AOD；(3)分别在OM，ON 上截取OE=OB，OF=OC；(4)依次连接DE，EF，FD，△ DEF 就是所求作的三角形，如图23.1-4．DEBFCA如何确定它们的旋转中心位置？答：找到两条对应点连线段的垂直平分线的交点.1. 练一练2. 下图为 4×4 的正方形网格，每个小正方形的边长均为 1，将 △OAB 绕点 O 逆时针旋转 90°，你能画出△OAB 旋转后的图形 △O'A'B'吗？ A＇B＇ABOA＇B＇3. 如图，怎样将右边的图案变成左边的图案？答：以右边图案的中心为旋转中心，将图案按逆时针方向旋转90°，然后平移，即可得到左边的图案.例3 如图，点A，C的坐标分别为（1，1），（2，4），将△ABC绕点A按逆时针方向旋转90°，得到△AB'C'，则点C的对应点C'的坐标为（　　）A．（－2，4）B．（4，0）C．（－2，2）D．（－1，3）C分析：根据题意画出图形，然后结合直角坐标系即可得出C'的坐标．典例精析4.如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（　　）A．（2，10）B．（－2，0）C．（2，10）或（－2，0）D．（10，2）或（－2，0）分析：要注意分顺时针旋转和逆时针旋转两种情况讨论解答．C练一练方法点拨：关于平面直角坐标系中的图形旋转后对应点的坐标的计算，通常要结合已知点及其对应点构造直角三角形，利用旋转的性质，证明所构造的两个直角三角形全等即可解决.选择不同的__________、不同的______旋转同一个图案,会出现不同的效果.(1)两个旋转中，旋转中心不变, ______改变了，产生了_______的旋转效果.旋转中心旋转角旋转角不同oa(2)两个旋转中,旋转角不变,__________改变了，产生了_______的旋转效果.旋转中心不同ooo 例4.如图(2)是某一种花的花瓣和中心，现以 O 为旋转 中 心画出分别旋转 45°， 90° ，135° ，180° ， 225°， 270°， 315°的这种花的图形． 解：如图(2).OO图（1）图（2）典例精析 本题是将基本图形按旋转图形的作法，分别按七个角度作旋转图形.作旋转图形时注意旋转三要素：旋转中心、旋转方向、旋转角.5.如图，在图①②③中，能通过旋转得到右侧图形的有(　　) A．①② B．①③ C．②③ D．①②③B练一练1. 如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A(－2，5)的对应点A′的坐标是(　　) A．(2，5) 　　 B．(5，2) C．(2，－5) 　　 D．(5，－2)B当堂练习 B.C. D.2. 将△AOB绕点O旋转180°得到△DOE，则下列作图正确的是（ ）C3．(2021·青岛)如图，将△ABC先向上平移1个单位长度，再绕点P按逆时针方向旋转90°，得到△A′B′C′，则点A的对应点A′的坐标是(　　)A．(0，4) B．(2，－2)C．(3，－2) D．(－1，4)D4.(2021·赤峰)下列图形绕某一点旋转一定角度都能与原图形重合，其中旋转角度最小的是(　　)C··5.如图，等边三角形ABC内有一点O，已知OA=4， OB=3，OC=5.求∠AOB的度数.解：将△BOA绕点B顺时针旋转60°得△BPC，连接OP，如图，由旋转的性质得BP=BO，∠OBP=60°.∴△OBP 为等边三角形，∴OP=OB=3.由旋转的性质得PC=OA=4.∵在△OPC 中，OP2+PC2=32+42 =OC2.∴∠OPC=90°，∴∠CPB=∠OPB+∠OPC=60°+90°=150°，∵旋转后的图形与旋转前的图形全等，∴∠AOB=∠CPB=150°.6．(2020·鄂尔多斯)(1)【操作发现】如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．①请按要求画图：将△ABC绕点A顺时针方向旋转90°，点B的对应点为点B′，点C的对应点为点C′.连接BB′.②在①中所画图形中，∠AB′B＝________°.解：如图①，△AB′C′即为所求．45(2)【问题解决】如图②，在Rt△ABC中，BC＝1，∠C＝90°，延长CA到点D，使CD＝1，将斜边AB绕点A顺时针旋转90°到AE，连接DE，求∠ADE的度数．解：如图②，过点E作EH⊥CD，交CD的延长线于点H.∵∠C＝∠BAE＝∠H＝90°，∴∠B＋∠CAB＝90°，∠CAB＋∠EAH＝90°.∴∠B＝∠EAH.又∵AB＝AE，∴△ABC≌△EAH(AAS)．∴BC＝AH，EH＝AC.∵BC＝CD，∴CD＝AH. ∴DH＝AC＝EH.∴∠EDH＝45°. ∴∠ADE＝135°.旋转的作图作旋转图形的步骤作图基本步骤五步：1.明确三要素;2.找出关键点;3.作出对应点;4.作出新图形;5.写出结论确定旋转中心找两条对应点连线段的垂直平分线的交点THANKS“”