人教版九年级上册24.1.4 圆周角优秀课件ppt

这是一份人教版九年级上册24.1.4 圆周角优秀课件ppt，共53页。

(1)知道什么是圆周角，并能从图形中准确识别它.(2)探究并掌握圆周角定理及其推论.(3)体会“由特殊到一般”“分类” “化归”等数学思想.
问题1 什么叫圆心角？指出图中的圆心角？
顶点在圆心的角叫圆心角, ∠BOC.
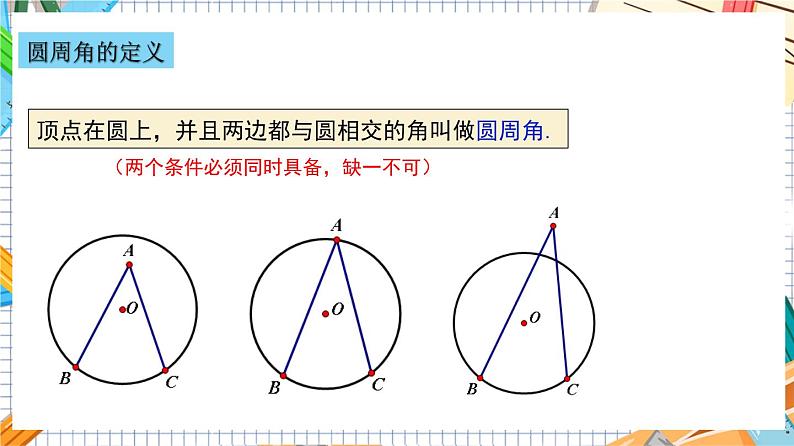
问题2 如图，∠BAC的顶点和边有哪些特点?
∠BAC的顶点在☉O上，角的两边分别交☉O于B、C两点.
顶点在圆上，并且两边都与圆相交的角叫做圆周角.
（两个条件必须同时具备，缺一不可）
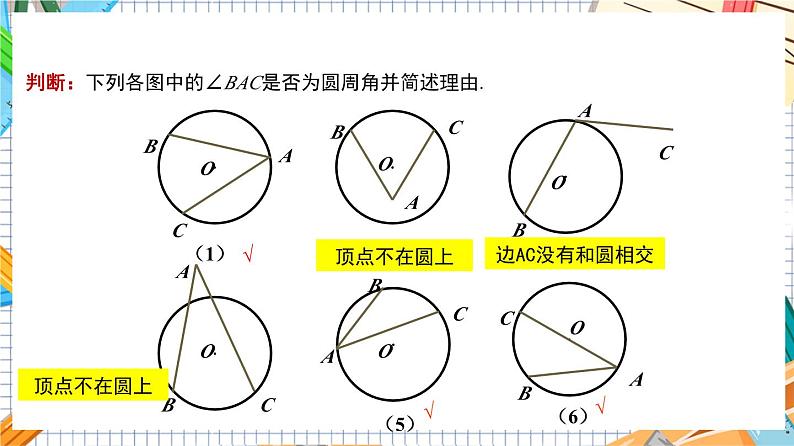
判断：下列各图中的∠BAC是否为圆周角并简述理由.
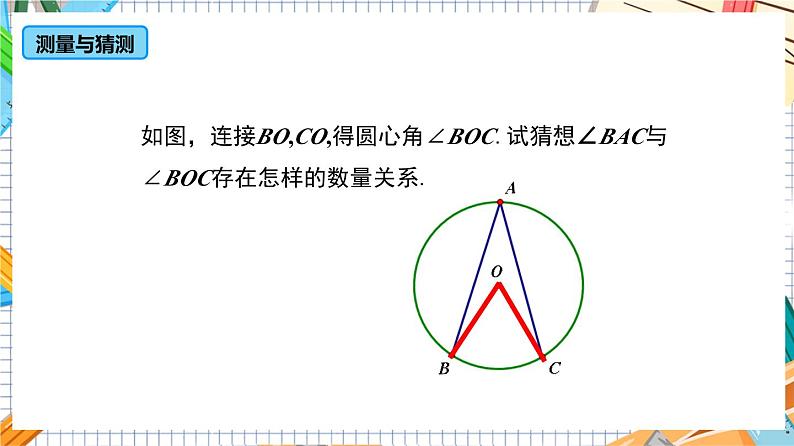
如图，连接BO,CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
圆心O 在∠BAC的 内部
圆心O在∠BAC的一边上
圆心O在∠BAC的外部
圆心O在∠BAC的一边上（特殊情形）
∠BOC= ∠ A+ ∠C
圆心O在∠BAC的内部
圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半.
问题1 如图，OB，OC都是⊙O的半径，点A ，D 是⊙O上任意两点，连接AB，AC，BD，CD.∠BAC与∠BDC相等吗？请说明理由.
∴∠BAC=∠BDC.
同弧或等弧所对的圆周角相等.
如图，线段AB是☉O的直径，点C是☉O上的任意一点（除点A、B外），那么∠ACB就是直径AB所对的圆周角.想一想，∠ACB会是怎样的角？
解：∵AB是直径，点O是圆心，∴∠AOB=180°.∵∠ACB是直径AB所对的圆周角，∴∠ACB= ∠AOB=90°.
能不能直接运用圆周角定理解答？
半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径.
例1 如图，分别求出图中∠x的大小.
解：(1)∵同弧所对圆周角相等，∴∠x=60°.
∵同弧所对圆周角相等，
∴∠ABF=∠D=20°，∠FBC=∠E=30°.
∴∠x=∠ABF+∠FBC=50°.
例2 如图，AB是⊙O的直径，弦CD交AB于点P，∠ACD=60°，∠ADC=70°.求∠APC的度数.
解：连接BC，则∠ACB=90°.
∴∠DCB＝∠ACB－∠ACD＝90°－60°=30°.
∴∠BAD=∠DCB=30°.
∴∠APC=∠BAD＋∠ADC＝30°＋70°＝100°.
例3 如图，⊙O的直径AB为10 cm，弦AC为6 cm．∠ACB的平分线交⊙O于点D, 求BC，AD，BD的长．
∴ ∠ACB=∠ADB=90°.
又在Rt△ABD中，AD2+BD2=AB2，
∴ ∠AOD=∠BOD.
∴∠ACD=∠BCD.
1. 如图，AB是⊙O的直径，∠A＝10°，则∠ABC＝______．
2. 如图,正方形ABCD的顶点都在☉O上,P是弧DC上的一点,则∠BPC=_____.
解析：连接BD,则BD是直径,∴△BCD是等腰直角三角形,∴∠BDC=45°,∴∠BPC=∠BDC=45°.
3. 如图，BD是⊙O的直径，∠CBD＝30°，则∠A的度数为(　　)A．30° B．45° C．60° D．75°
如果一个多边形所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.
如图，四边形ABCD为⊙O的内接四边形，⊙O为四边形ABCD的外接圆.
猜想：∠A与∠C, ∠B与∠D之间的关系为：
∠A+ ∠C=180º，∠B+ ∠D=180º.
想一想：如何证明你的猜想呢？
∵ ∠A所对的圆心角是∠β，∠C所对的圆心角是∠α，则 又
同理
性质：圆的内接四边形的对角互补.
4．四边形ABCD是⊙O的内接四边形，且∠A=110°，∠B=80°，则∠C= ，∠D= .5．⊙O的内接四边形ABCD中，∠A∶∠B∶∠C=1∶2∶3 ，则∠D= .
例4 如图，AB为⊙O的直径，CF⊥AB于E，交⊙O于D，AF交⊙O于G. 求证：∠FGD＝∠ADC.
证明：∵四边形ACDG内接于⊙O，∴∠FGD＝∠ACD.又∵AB为⊙O的直径，CF⊥AB，∴AB垂直平分CD.∴AC＝AD.∴∠ADC＝∠ACD.∴∠FGD＝∠ADC.
方法总结：圆内接四边形的性质是推导角相等关系的重要依据．
6. 如图，在⊙O的内接四边形ABCD中，∠BOD＝120°，那么∠BCD是(　　)A．120° B．100°C．80° D．60°
1.如图，⊙O中，弦BC与半径OA相交于点D，连接AB，OC．若∠A=60°，∠ADC=85°，则∠C的度数是（　　）A．25° B．27.5°C．30° D．35°
2.如图，点B，C，D在⊙O上，若∠BCD=130°，则∠BOD的度数是（ ）A．50°B．60°C．80°D．100°
解析：圆上取一点A，连接AB，AD， ∵点A、B、C、D在⊙O上∠BCD=130°， ∴∠BAD=50°， ∴∠BOD=100°
(2)证明：在BM上截取BE＝BC，连结CE，如图②，∵∠MBC＝60°，BE＝BC，∴△EBC是等边三角形，∴CE＝CB＝BE，∠BEC＝60°，∴∠MEC＝120°＝∠ABC.又∵∠BAC＝∠BMC，∴△ABC≌△MEC，∴AB＝ME.∵ME＋EB＝BM，∴AB＋BC＝BM
1．(3分)如图，∠APB是圆周角的是( )
2．(3分)(浉河区期末)如图，点A，B，C在⊙O上，若∠OAB＝54°，则∠C的度数为( )A．54° B．27° C．36° D．46°
3．(3分)(长葛市一模)如图，以原点O为圆心的圆交x轴于点A，B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB＝25°，则∠OCD的度数是( )A．45° B．60° C．65° D．70°
4．(3分)(洛宁县期末)如图，已知圆周角∠ACB＝130°，则圆心角∠AOB＝________．
5．(8分)如图，已知A，B，C，D是⊙O上的四个点，AB＝BC，BD交AC于点E，连结CD，AD.求证：DB平分∠ADC.
6.如图，⊙O中，弦AD平行于弦BC，∠AOC=78°，求∠DAB的度数．解：∵AD∥BC， ∴∠DAB=∠B.又∵∠B= ∠AOC=39°. ∴∠DAB=39°.
7.如图，⊙O的半径为1，A,B,C是⊙O上的三个点，且∠ACB=45°，求弦AB的长.解：连接OA、OB.∵∠ACB=45°,∴∠BOA=2∠ACB=90°.又OA=OB, ∴△AOB是等腰直角三角形.
8.如图，A,P,B,C是⊙O上的四点，∠APC=∠CPB=60°，判断△ABC的形状并证明你的结论.解：△ABC是等边三角形. 证明如下：∵∠APC=∠ABC=60°， ∠CPB=∠BAC=60°，∴∠ACB=180°- ∠ABC-∠BAC=60°，∴△ABC是等边三角形.
9.如图，已知A，B，C，D是⊙O上的四点，延长DC，AB相交于点E，若BC=BE．求证：△ADE是等腰三角形．证明：∵∠A+∠BCD=180°, ∠BCE+∠BCD=180°. ∴∠A=∠BCE. ∵BC=BE, ∴∠E=∠BCE, ∴∠A=∠E, ∴AD=DE, ∴△ADE是等腰三角形.
10.如图，已知EF是⊙O的直径，把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上，斜边AB与⊙O交于点P，点B与点O重合；将三角形ABC沿OE方向平移，使得点B与点E重合为止．设∠POF=x°，则x的取值范围是 ．
11．(10分)如图，AB是⊙O的直径，D，E为⊙O上位于AB异侧的两点，连结BD并延长至点C，使得CD＝BD，连结AC交⊙O于点F，连结AE，DE，DF.(1)求证：∠E＝∠C；(2)若∠E＝55°，求∠BDF的度数．解：(1)证明：连结AD，∵AB是⊙O的直径，∴∠ADB＝90°，即AD⊥BC.∵CD＝BD，∴AD垂直平分BC，∴AB＝AC，∴∠B＝∠C.∵∠B＝∠E，∴∠E＝∠C(2)∵四边形AEDF是⊙O的内接四边形，∴∠AFD＝180°－∠E.∵∠CFD＝180°－∠AFD，∴∠CFD＝∠E＝55°，由(1)得∠E＝∠C＝55°，∴∠BDF＝∠C＋∠CFD＝55°＋55°＝110°
12．(12分)(洛宁县三模)如图，AB为⊙O的直径，C为⊙O上半圆的一个动点，CE⊥AB于点E，∠OCE的角平分线交⊙O于点D.(1)当点C在⊙O上半圆移动时，点D的位置会变吗？请说明理由；(2)若⊙O的半径为5，弦AC的长为6，连结AD，求线段AD，CD的长．