




人教版九年级上册24.2.1 点和圆的位置关系获奖ppt课件
展开1.理解并掌握点和圆的三种位置关系.(重点)2.理解不在同一直线上的三个点确定一个圆及其运用. (重、难点) 3.了解三角形的外接圆和三角形外心的概念. (难点) 4.了解反证法的证明思想.
问题 2020年东京奥运会我国射击运动员杨倩获10米气步枪首枚金牌,为我国赢得荣誉.如图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
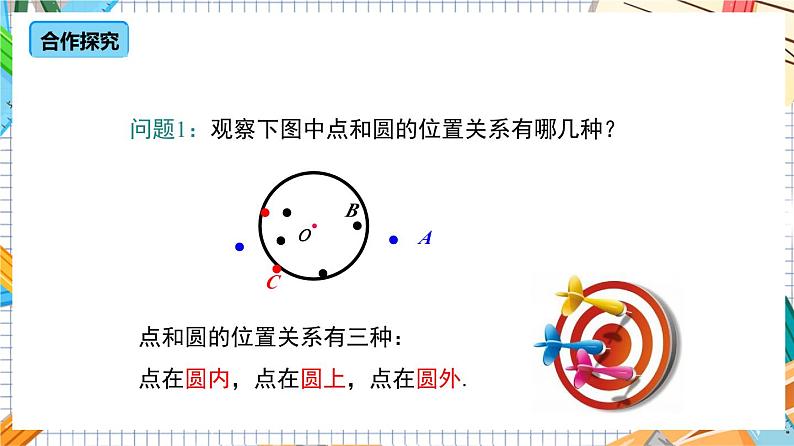
问题1:观察下图中点和圆的位置关系有哪几种?
点和圆的位置关系有三种:点在圆内,点在圆上,点在圆外.
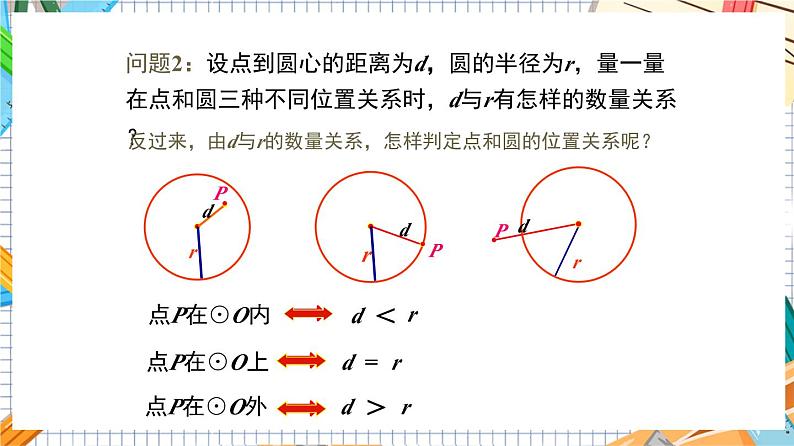
问题2:设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
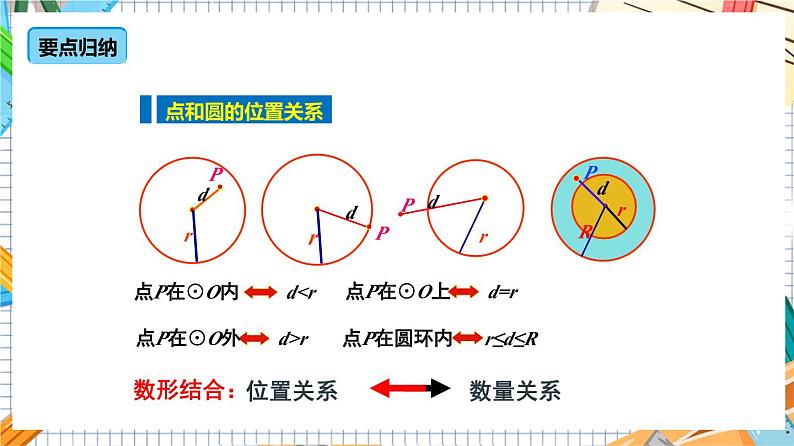
点P在⊙O内
点P在⊙O上
点P在⊙O外
反过来,由d与r的数量关系,怎样判定点和圆的位置关系呢?
1. ⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
2. 圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )A.大圆内 B.小圆内 C.小圆外 D.大圆内,小圆外
例1 如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
解:AD=4=r,故点D在⊙A上; AB=3
(2)若以点A为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
问题1:如何过一个点A作一个圆?过点A可以作多少个圆?
以不与点A重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;可作无数个圆.
问题2:如何过两点A、B作一个圆?过两点可以作多少个圆?
作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;可作无数个圆.
问题3:过不在同一直线上的三点能不能确定一个圆?
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
定理: 不在同一直线上的三个点确定一个圆.
试一试:已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
3. 如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.
∵A、B两点在圆上,所以圆心必与A、B两点的距离相等,
又∵和一条线段的两个端点距离相等的点在这条线段的垂直平分线上,
∴圆心在CD所在的直线上,因此可以做任意两条直径,它们的交点为圆心.
1. 外接圆⊙O叫做△ABC的________, △ABC叫做⊙O的____________.
到三角形三个顶点的距离相等.
2.三角形的外心:定义:
三角形外接圆的圆心叫做三角形的外心.
三角形三边垂直平分线的交点.
判一判:下列说法是否正确(1)任意的一个三角形一定有一个外接圆( )(2)任意一个圆有且只有一个内接三角形( )(3)经过三点一定可以确定一个圆( )(4)三角形的外心到三角形各顶点的距离相等( )
画一画:分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内,直角三角形的外心为直角三角形斜边的中点,钝角三角形的外心位于三角形外.
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学应该建在哪个位置?你怎么确定这个位置呢?
解:学校应该建在AB和AC垂直平分线的交点上
4. 如图,已知直角坐标系中,A(0,4), B(4,4), C(6,2).
(1)写出经过A,B,C三点的圆弧所在圆的圆心M的坐标.(2)判断点D(5,-2)和圆M的位置关系.
解:(1)在方格纸中,线段AB和BC的垂直平分线相交于点(2,0),所以圆心M的坐标为(2,0).(2)圆的半径线段DM ,所以点D在圆M内.
例2 如图,在△ABC中,O是它的外心,BC=24 cm,O到BC的距离是5 cm,求△ABC的外接圆的半径.
解:连接OB,过点O作OD⊥BC于点D,
即△ABC的外接圆的半径为13cm.
5. 在Rt△ABC中,∠C=90°,AC=6 cm,BC=8cm,则它的外心与顶点C的距离为( )A.5 cm B.6 cm C.7 cm D.8 cm
思考:经过同一条直线上的三个点能作出一个圆吗?
如图,假设经过同一条直线l上A、B、C三点可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l,这与我们以前学过的“平面内,过一点有且只有一条直线与已知直线垂直”矛盾,所以过同一条直线上的三点不能作圆.
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
假设命题的结论不成立从这个假设出发,经过推理,得出矛盾由矛盾判定假设不正确,从而肯定命题的结论正确
例3 求证:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC.求证:△ABC中至少有一个内角小于或等于60°.
证明:假设 ,则 .∴ ,即 .这与 矛盾,假设不成立.∴ .
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
∠A+∠B+∠C>180°
三角形的内角和为180°
△ABC中至少有一个内角小于或等于60°
∠A+∠B+∠C>60°+60°+60°=180°
6. 利用反证法证明“在直角三角形中,至少有一个锐角不大于45°”时,应先假设( )A.有一个锐角小于45° B.每一个锐角都小于45°C.有一个锐角大于45° D.每一锐角都大于45°
1.(临沂中考)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC的外接圆的半径.
1.(3分)已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是为( )A.点P在圆内 B.点P在圆上C.点P在圆外 D.不能确定2.(3分)(三门峡期中)在△ABC中,∠C=90°,以点B为圆心,以BC长为半径作圆,点A与该圆的位置关系为( )A.点A在圆外 B.点A在圆内C.点A在圆上 D.无法确定
3.(3分)已知⊙O的半径为3,点P到⊙O的圆心的距离是方程x2-5x+6=0的根,则点P与⊙O的位置关系是( )A.点P在圆内 B.点P在圆上C.点P在圆外 D.点P在圆内或圆上
4.(3分)⊙O的半径r=5 cm,圆心到直线l的距离OM=4 cm,在直线l上有一点P,且PM=3 cm,则点P在⊙O________.
5.(10分)如图,在Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,以点B为圆心,BC长为半径作⊙B,确定点A,C及AB中点M与⊙B的位置关系.
6.(3分)已知A,B,C是平面内的三点,AB=3,BC=3,AC=6,下列说法正确的是( )A.可以画一个圆,使A,B,C都在圆上B.可以画一个圆,使A,B在圆上,C在圆外C.可以画一个圆,使A,C在圆上,B在圆外D.可以画一个圆,使B,C在圆上,A在圆内
7.(4分)如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是点_____.
8.(3分)如果一个三角形的外心在它的一条边上,那么此三角形必是( )A.锐角三角形 B.直角三角形C.钝角三角形 D.等边三角形
9.(4分)下列命题正确的是( )①经过三点一定可以作圆;②三角形三边的垂直平分线的交点是三角形的外心;③一个圆只有一个内接三角形;④三角形的外心到三角形各顶点的距离相等;⑤三角形的外心到三边的距离相等.A.①②③ B.①③⑤ C.②④ D.②⑤
14.平面上一点到⊙O上一点的距离最长为6 cm,最短为2 cm,则⊙O的半径为_______cm.15.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是______.
16.(10分)如图,已知矩形ABCD的边长AB=3 cm,AD=4 cm.(1)以点A为圆心,4 cm为半径作⊙A,则点B,C,D与⊙A有怎样的位置关系?(2)若以A为圆心作⊙A,使B,C,D三点中至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
17.(12分)如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连结AE.(1)求证:四边形AECD为平行四边形;(2)连结CO,求证:CO平分∠BCE.
解:(1)证明:由圆周角定理得,∠B=∠E,又∠B=∠D,∴∠E=∠D.∵CE∥AD,∴∠D+∠ECD=180°,∴∠E+∠ECD=180°,∴AE∥CD,∴四边形AECD为平行四边形(2)∵四边形AECD为平行四边形,∴AD=CE,又∵AD=BC,∴CE=BC,作OM⊥BC于点M,ON⊥CE于点N,∴OM=ON,又OM⊥BC,ON⊥CE,∴CO平分∠BCE
定理:过不在同一直线上的三个点确定一个圆
直角三角形的外心在斜边中点处
注意:同一直线上的三个点不能作圆
初中数学人教版九年级上册24.2.1 点和圆的位置关系图片ppt课件: 这是一份初中数学人教版九年级上册24.2.1 点和圆的位置关系图片ppt课件,共24页。PPT课件主要包含了点和圆的位置关系,点在圆内,d﹤r,点在圆上,点在圆外,d=r,练一练,﹤r﹤5,不能作出,为什么等内容,欢迎下载使用。
数学九年级上册24.2.1 点和圆的位置关系教学课件ppt: 这是一份数学九年级上册24.2.1 点和圆的位置关系教学课件ppt,共23页。PPT课件主要包含了学习目标,情景引入,知识精讲,针对练习,数形结合,位置关系,数量关系,典例解析,达标检测,小结梳理等内容,欢迎下载使用。
初中数学人教版九年级上册24.2.1 点和圆的位置关系教课课件ppt: 这是一份初中数学人教版九年级上册24.2.1 点和圆的位置关系教课课件ppt,共25页。PPT课件主要包含了课堂练习等内容,欢迎下载使用。













