人教版数学九年级上册24.3《正多边形的画法》（第2课时）课件

这是一份人教版数学九年级上册24.3《正多边形的画法》（第2课时）课件，共22页。

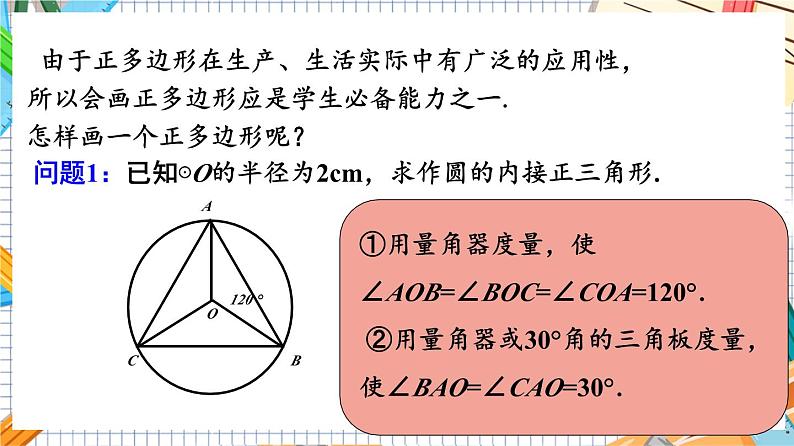
24.3正多边形的画法（第2课时）第24章 圆人教版数学九年级上册1. 掌握正多边形的画法.2. 掌握画正多边形的关键——等分圆周的两种方法：一是量角器等分圆周；二是用尺规作图等分圆周.学习目标实际生活中，经常遇到画正多边形的问题，比如画一个六角螺帽的平面图、画一个五角星等，这些问题都与等分圆周有关，要制造下图中的零件，也需要等分圆周. 由于正多边形在生产、生活实际中有广泛的应用性，所以会画正多边形应是学生必备能力之一.怎样画一个正多边形呢？ 问题1：已知⊙O的半径为2cm，求作圆的内接正三角形.120 °①用量角器度量，使∠AOB=∠BOC=∠COA=120°． ②用量角器或30°角的三角板度量，使∠BAO=∠CAO=30°． AOCB你能用以上方法画出正四边形、正五边形、正六边形吗？·ABCDOOABCDEF·90°72°60°正四边形：如下图所示，在 中用直尺和圆规作两条互相垂直的直径，就可以把 四等分，从而作出正四边形；正八边形：再用直尺和圆规分别作与正四边形相邻两边垂直的直径，就可以作出正八边形，如上图所示.正十六边形：同理可以作出正十六边形等边数逐次倍增的正多边形.动手试一试正六边形：如下图所以，先画 的任意一条直径AB，再分别以点A，B为圆心，以 的半径R为半径画弧，与 相交于点C，D和E，F，顺次连接点A，C，E，B，F，D，A，得正六边形ACEBFD；正十二边形：在正六边形的基础上可作正十二边形，如右图所示；正三角形：连接BD，BC，CD，得正三角形，如下图所示.我们不难发现，随着边数的增加，正多边形越来越接近于圆，正多边形将越来越难画说说作正多边形的方法有哪些?（1）用量角器等分圆周作正n边形； （2）用尺规作正方形及由此扩展作正八边形, 用尺规作正六边形及由此扩展作正12边形、正三角形． 例 已知☉O和☉O上的一点A(如图).求作☉O的内接正方形ABCD和内接正六边形AEFCGH;正多边形的画法解：作法:①作直径AC;②作直径BD⊥AC;③依次连接A、B、C、D四点.∴四边形ABCD即为☉O的内接正方形.④分别以A、C为圆心,OA的长为半径作弧,交☉O于E、H、F、G;⑤顺次连接A、E、F、C、G、H各点;∴六边形AEFCGH为☉O的内接正六边形,如图所示.AO.. 画一个半径为2cm的正五边形，再作出这个正五边形的各条对角线，画出一个五角星.1.图1是我国古代建筑中的一种窗格，其中冰裂纹图案象征着坚冰出现裂纹并开始消溶，形状无一定规则，代表一种自然和谐美．图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形，则∠1+∠2+∠3+∠4+∠5= 度连接中考解析：由多边形的外角和等于360°可知，∠1+∠2+∠3+∠4+∠5=360°.　360　   D  2．(平阳县一模)我国古代伟大的数学家刘徽于公元263年撰《九章算术注》中指出，“周三径一”不是圆周率值，实际上是圆内接正六边形周长和直径的比值．刘徽发现，圆内接正多边形边数无限增加时，多边形的周长就无限逼近圆周长，从而创立“割圆术”，为计算圆周率建立起相当严密的理论和完善的算法．如图，六边形ABCDEF是圆内接正六边形，把每段弧二等分，作出一个圆内接正十二边形，连结AG，CF，AG交CF于点P， D C 1.画正多边形的方法：由于同圆中相等的圆心角所对的弧相等，因此作相等的圆心角就可以等分圆周，从而得到相应的正多边形.2.画正多边形的方法1.用量角器等分圆2.尺规作图等分圆THANKS“”