2023八年级数学下册第一章三角形的证明等边三角形课时测试新版北师大版

等边三角形

时间  40分钟  总分  100分

一、选择题(每题5分)

1.不能判定两个等边三角形全等的是（  ）

A．一条边对应相等      B．一个内角对应相等

C．一边上的高对应相等  D．有一内角的角平分线对应相等

【答案】B

【解析】

试题分析：根据等边三角形的性质和全等三角形的判定方法进行判断.

解：A选项、一条边对应相等的两个等边三角形的三边都对应相等，根据SSS可证这两个等边三角形全等；

B选项、一个内角对应相等的两个等边三角形的三个角都对应相等，但是边长不一定相等，所以不能判断两个等边三角形全等；

C选项、一边上的高对应相等的两个等边三角形的三条边都相等，根据SSS可证这两个等边三角形全等；

D选项、有一内角的角平分线对应相等的两个等边三角形的三条边都相等，根据SSS可证这两个等边三角形全等.

故应选B.

考点：1.等边三角形的性质；2.全等三角形的判定

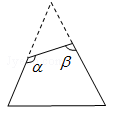
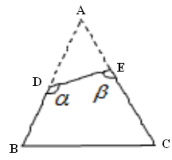
2.如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β的度数是（　　）

A. 180°        B. 220°        C. 240°        D. 300°

【答案】C

【解析】

试题分析：根据等边三角形的性质可得：∠A=∠B=∠C=60°，根据三角形内角和定理可得∠ADE+∠AED=120°，因为∠ADE+∠BDE+∠AED+∠CED=360°，所以可得∠α+∠β=240°.

解：∵△ABC是等边三角形，

∴∠A=∠B=∠C=60°，

∴∠ADE+∠AED=120°，

∵∠ADE+∠BDE+∠AED+∠CED=360°，

∴∠BDE+∠CED=240°，

∴∠α+∠β=240°.

故应选C.

考点：等边三角形的性质

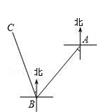
3.一艘轮船由海平面上A地出发向南偏西40°的方向行驶40海里到达B地，再由B地向北偏西20°的方向行驶40海里到达C地，则A、C两地相距（　　）

A．30海里        B.40海里        C.50海里        .60海里

【答案】B

【解析】

试题分析：根据两次航行的方向角可得：∠ABC=60°，根据AB=AC，可得△ABC是等边三角形，根据等边三角形的性质可以得到A、C两地的距离.

解：∵∠ABC=60°，AB=AC，

∴△ABC是等边三角形，

∴AC=AB=40.

故答案是B.

考点：等边三角形的判定和性质

二、填空题(每题5分)

4.在△ABC中，AB=AC，

① 如果∠A＝70°，则∠C＝_________，∠B＝___________；

② 如果∠A＝90°，则∠B＝_________，∠C＝___________；

③ 如果∠A＝60°，则∠B＝_________，∠C＝___________。

【答案】①55°；55°；②45°；45°；③60°；60°.

【解析】

试题分析：根据等腰三角形的性质和三角形内角和定理解答.

解：①∵△ABC中，AB=AC，

∴∠B=∠C，

∵∠A＝70°，

∴∠B=∠C＝55°；

②∵△ABC中，AB=AC，

∴∠B=∠C，

∵∠A＝90°，

∴∠B=∠C＝45°；

③∵△ABC中，AB=AC，

∴∠B=∠C，

∵∠A＝60°，

∴∠B=∠C＝60°.

故答案是①55°；55°；②45°；45°；③60°；60°.

考点：1.等腰三角形的性质；2.三角形内角和定理

5.一个等边三角形的周长是21cm，它的边长=_______cm。

【答案】7

【解析】

试题分析：根据等边三角形的三边相等解答.

解：∵等边三角形的三边相等，

∴等边三角形的边长=×21=7.

故答案是7.

考点：等边钱的性质

6.如图，以A，B两点为其中两个顶点作位置不同的等边三角形，最多可以作出　_________　个．

【答案】2

【解析】

试题分析：根据线段的垂直平分线的性质和等边三角形的性质解答.

解：到点A、B距离相等的点在AB的垂直平分线上，

到点A、B的距离相等且等于AB的长度的点有两个，

所以最多可以作出两个等边三角形.

故答案是2.

考点：等边三角形

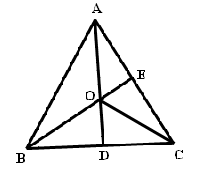
7.O是等边△ABC两条高的交点，若△AOB的面积为1，则△ABC的面积为_____．

【答案】3

【解析】

试题分析：

解：如下图所示，根据等边三角形的性质可得：

△AOB≌△AOC≌△BOC，

∵△AOB的面积为1，

∴△ABC的面积为3.

故答案是3.

考点：等边三角形的性质

8.如图所示，P是等边三角形ABC内一点，将△ABP绕点B顺时针方向旋转60°，得到△CBP′，若PB=3，则PP′=　_________　．

【答案】3

【解析】

试题分析：根据旋转的性质可得：△BPP′是等边三角形，根据等边三角形的性质求出PP′.

解：根据旋转的性质可得：△ABP≌△CBP′，

∴BP=BP′，

∵旋转角是60°，

∴△BPP′是等边三角形，

∴PP′=BP=3.

故答案是3.

考点：1.旋转的性质；2.等边三角形的性质.

三、解答题(每题15分)

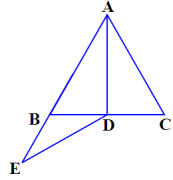
9.如图，等边三角形ABC中，AD是BC上的高，延长AB到点E，使BE=BD，连接DE.

求证：△ADE是等腰三角形.

【答案】证明见解析

【解析】

试题分析：根据等边三角形的性质求出∠BAD的度数，根据三角形外角和定理求出∠E的度数，根据等边对等角可证结论成立.

证明：∵△ABC是等边三角形，

∴∠A=∠ABC=∠ACB=60°，

∵AD是中线，∴∠BAD=30°，

∵BE=BD，

∴∠E=∠BDE，

∵∠ABD=∠E+∠BDE，

∴∠E=30°，

∴AD=ED ，

∴△ADE是等腰三角形.

考点：1.等边三角形的性质；2.三角形外角定理

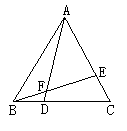
10.如图所示，在等边△ABC中，在边BC，AC上取BD=CE，连接AD，BE交于F.

求证∠AFE=60°

【答案】证明见解析

【解析】

试题分析：根据等边三角形的性质可得：BC=AB，∠C=∠ABD，根据SAS可证△ABD≌△BCE，根据全等三角形的性质可证∠BAD=∠CBE，所以∠BAD+∠ABE=60°，所以∠AFE=60°.

解：∵△ABC是等边三角形，

∴BC=AB，∠C=∠ABD，

在△ABD和△BCE中，

，

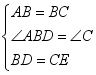∴△ABD≌△BCE，

∴∠BAD=∠CBE，

∵∠ABD+∠CBE=60°，

∴∠BAD+∠ABE=60°，

∴∠AFE=∠BAD+∠ABE=60°.

考点：1.等边三角形的性质；2.全等三角形的判定与性质

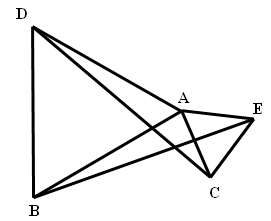
11.如图ᅀABD和ᅀACE都是等边三角形。求证  BE=DC

【答案】证明见解析

【解析】

试题分析：根据等边三角形的性质可得：AB=AC，AE=AC，∠DAC=∠BAE，根据SAS可证△ADC≌△ABE，根据全等三角形的性质证明结论成立.

证明：∵△ABD和△ACE是等边三角形，

∴AB=AC，AE=AC，∠DAB=∠CAE=60°，

∴∠DAC=∠BAE，

在△ADC和△ABE中，

，

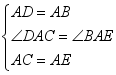∴△ADC≌△ABE，

∴BE=DC.

考点：1.等边三角形的性质；2.全等三角形的判定和性质

12.如图，点C是线段AB上除点A、B外的任意一点，分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE，连接AE交DC于M，连接BD交CE于N，连接MN．

（1）求证：AE=BD；

（2）求证：MN∥AB．

【答案】(1)证明见解析；(2)证明见解析

【解析】

试题分析：(1)根据等边三角形的性质可得：AC=DC，CE=CB，∠DCA=60°，∠ECB=60°，所以可得：∠ACE=∠DCB，利用SAS可证△ACE≌△DCB，根据全等三角形的性质证明结论成立；

(2)根据全等三角形的性质可证∠CAM=∠CDN，根据∠ACD=∠ECB=60°，可求∠DCN=60°，利用ASA可证△ACM≌△DCN，所以可证△MCN为等边三角形，根据等边三角形的性质可得∠NMC=∠DCN=60°，根据内错角相等两直线平行可证结论成立.

证明：（1）∵△ACD和△BCE是等边三角形，

∴AC=DC，CE=CB，∠DCA=60°，∠ECB=60°，

∵∠DCA=∠ECB=60°，

∴∠DCA+∠DCE=∠ECB+∠DCE，

∴∠ACE=∠DCB，

在△ACE与△DCB中，

∵，

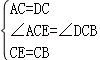∴△ACE≌△DCB，

∴AE=BD；

（2）∵由（1）得，△ACE≌△DCB，

∴∠CAM=∠CDN，

∵∠ACD=∠ECB=60°，而A、C、B三点共线，

∴∠DCN=60°，

在△ACM与△DCN中，

∵，

∴△ACM≌△DCN，

∴MC=NC，

∵∠MCN=60°，

∴△MCN为等边三角形，

∴∠NMC=∠DCN=60°，

∴∠NMC=∠DCA，

∴MN∥AB．

考点：1.等边三角形的判定和性质；2全等三角形的判定和性质；3.平行线的判定