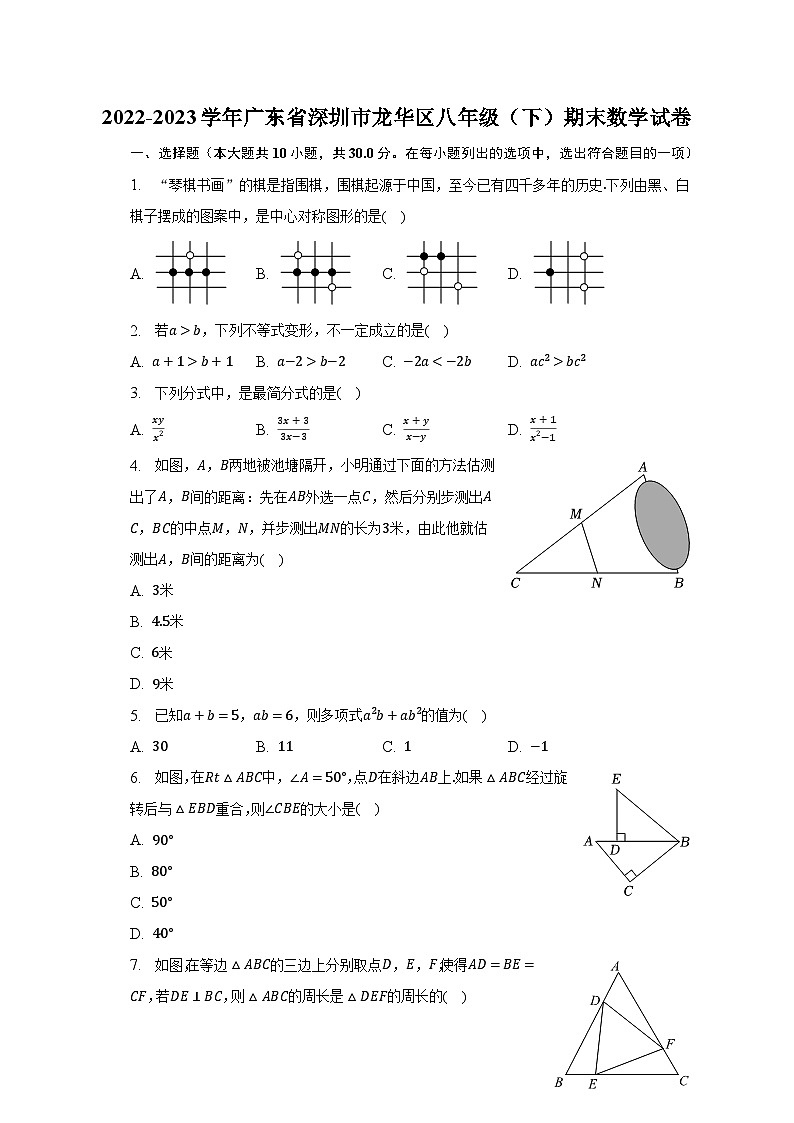
2022-2023学年广东省深圳市龙华区八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年广东省深圳市龙华区八年级（下）期末数学试卷（含解析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年广东省深圳市龙华区八年级（下）期末数学试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. “琴棋书画”的棋是指围棋，围棋起源于中国，至今已有四千多年的历史.下列由黑、白棋子摆成的图案中，是中心对称图形的是(    )
A. B. C. D.
2. 若a>b，下列不等式变形，不一定成立的是(    )
A. a+1>b+1 B. a−2>b−2 C. −2abc2
3. 下列分式中，是最简分式的是(    )
A. xyx2 B. 3x+33x−3 C. x+yx−y D. x+1x2−1
4. 如图，A，B两地被池塘隔开，小明通过下面的方法估测出了A，B间的距离：先在AB外选一点C，然后分别步测出AC，BC的中点M，N，并步测出MN的长为3米，由此他就估测出A，B间的距离为(    )
A. 3米
B. 4.5米
C. 6米
D. 9米
5. 已知a+b=5，ab=6，则多项式a2b+ab2的值为(    )
A. 30 B. 11 C. 1 D. −1
6. 如图，在Rt△ABC中，∠A=50°，点D在斜边AB上.如果△ABC经过旋转后与△EBD重合，则∠CBE的大小是(    )
A. 90°
B. 80°
C. 50°
D. 40°
7. 如图，在等边△ABC的三边上分别取点D，E，F，使得AD=BE=CF，若DE⊥BC，则△ABC的周长是△DEF的周长的(    )
A. 2倍
B. 3倍
C. 3倍
D. 2 3倍
8. 如图，在▱ABCD中，对角线AC与BD相交于点O，BD⊥AD，AB=5，BC=3，则以下结论不正确的是(    )

A. AD=3 B. OB=2
C. AC=2 13 D. ▱ABCD的面积为6
9. 根据规划设计，某工程队准备修建一条长1120米的盲道.由于情况改变，实际每天修建盲道的长度比原计划增加10米，结果提前2天完成了这一任务，假设原计划每天修建盲道x米，根据题意可列方程为(    )
A. 1120x−1120x+10=2 B. 1120x−1120x−10=2
C. 1120x+10−1120x=2 D. 1120x−10−1120x=2
10. 如图，l1//l2，直线l1与直线l2之间的距离为4，点A是直线l1与l2外一点，点A到直线l1的距离为2，点B，D分别是直线l1与直线l2上的动点，以点B为圆心，AD的长为半径作弧，再以点D为圆心，AB的长为半径作弧，两弧交于点C，则点A与点C之间距离的最小值为(    )
A. 6
B. 8
C. 10
D. 12
二、填空题（本大题共7小题，共21.0分）
11. 分解因式：a3+2a2+a= ______ ．
12. 由深圳到广州的一条铁路全程约为146千米，高铁全程运行时间为a小时，则高铁的速度是每小时______ 千米．
13. 一个多边形的内角和等于它的外角和，这个多边形是______边形．
14. 一次函数y=kx+b的图象如图所示，则不等式kx+b>0的解集为______ ．


15. 某校学生会组织七年级和八年级共30名同学参加环保志愿者活动，七年级学生平均每人收集15个废弃塑料瓶，八年级学生平均每人收集20个废弃塑料瓶.为了保证所收集的塑料瓶总数不少于500个.则七年级学生参加活动的人数至多是______ 名.
16. 我们把顶角为36°的等腰三角形称作“黄金三角形”，“黄金三角形”的底边长是腰长的 5−12倍.如图，△ABC是“黄金三角形”，AB=AC，AB的垂直平分线交AB于点D，交AC于点E，则△BCE与△ABE的面积比为______ ．


17. 如图，在四边形ABCD中，AD//BC，∠D=45°，将边AB绕点B顺时针旋转90°后，点A恰好落在边CD上的点E处，已知BC=2，则DE的长度为______ ．


三、解答题（本大题共8小题，共69.0分。解答应写出文字说明，证明过程或演算步骤）
18. (本小题8.0分)
解不等式组：2x−1”或“=”或“b，
∴a−2>b−2，
故B不符合题意；
C、∵a>b，
∴−2ab，c≠0，
∴ac2>bc2，
故D符合题意；
故选：D．
根据不等式的性质进行计算，逐一判断即可解答．
本题考查了不等式的性质，熟练掌握不等式的性质是解题的关键．

3.【答案】C 
【解析】解：A、 xyx2=yx，原分式不是最简分式，不符合题意；
B、3x+33x−3=x+1x−1，原分式不是最简分式，不符合题意；
C、x+yx−y是最简分式，符合题意；
D、x+1x2−1=x+1(x+1)(x−1)=1x−1，原分式不是最简分式，不符合题意．
故选：C．
根据最简分式的定义对各选项进行逐一分析即可．
本题考查的是最简分式，熟知一个分式的分子与分母没有公因式时，叫最简分式是解题的关键．

4.【答案】C 
【解析】解：∵AC，BC的中点是M，N，
∴MN是△ABC的中位线，
∴MN=12AB，
∵MN≈3米，
∴AB≈6米．
故选：C．
由三角形中位线定理得到MN=12AB，由MN的值，即可求出AB的长．
本题考查三角形中位线定理，掌握三角形中位线定理是解题的关键．

5.【答案】A 
【解析】解：由题意，a2b+ab2=ab(a+b)．
∵a+b=5，ab=6，
∴a2b+ab2=ab(a+b)=6×5=30．
故选：A．
依据题意，由a2b+ab2=ab(a+b)，结合已知条件代入数据即可得解．
本题考查了因式分解的应用，解题时要能将所求问题先进行因式分解，然后代入数据计算是关键．

6.【答案】B 
【解析】解：∵△ABC经过旋转后与△EBD重合，
∴∠CBA=∠EBD，
在Rt△ABC中，∠A=50°，
∴∠CBA=∠EBD=90°−50°=40°，
∴∠CBE=80°，
故选：B．
根据旋转的性质得出∠CBA=∠EBD，再根据直角三角形两锐角互余求出∠CBA=∠EBD=90°−50°=40°，即可求解．
本题考查了旋转的性质，明确旋转前后对应边、对应角相等是解题的关键．

7.【答案】C 
【解析】解：∵△ABC是等边三角形，AD=BE=CF，
∴AB=BC=CA，∠A=∠B=∠C=60°，
∴BD=CE=AF，
∴△ADF≌△BED≌△CFE(SAS)，
∴DF=ED=FE，
∴△DEF是等边三角形，
∵∠B=60°，DE⊥BC，
∴∠BDE=30°，∠ADF=∠BED=∠CFE=90°，
设AD=BE=CF=x，则AF=BD=CE=2x，
∴AB=x+2x=3x，DE= 3BE= 3x，
∴△ABC的周长=3AB=9x，
△DEF的面积=3DE=3 3x，
∴△ABC的周长是△DEF的周长 3倍．
故选：C．
先证明△ADF≌△BED≌△CFE，得到等边△DEF，设AD=BE=CF=x，则AF=BD=CE=2x，DE= 3x，进而即可解决问题．
本题考查了全等三角形的判定与性质，等边三角形的判定和性质，含30度角的直角三角形的性质，勾股定理，熟练掌握勾股定理，等边三角形的判定，直角三角形的性质是解题的关键．

8.【答案】D 
【解析】解：∵四边形ABCD是平行四边形，BC=3，
∴OD=OB，OA=OC，AD=BC=3，故A正确；
∵BD⊥AD，
∴∠ADB=90°，
∵AB=5，
∴BD= AB2−AD2= 52−32=4，
∴OB=OD=2，故B正确；
∴OA= AD2+OD2= 32+22= 13，
∴AC=2OA=2 13，故C正确；
∴平行四边形ABCD的面积为AD×BD=3×4=12，故D错误．
故选：D．
根据平行四边形的性质判断AD=BC=3；根据勾股定理求出BD判断OB=2；根据勾股定理求出AO判断AC的长；根据AD和BD的长计算平行四边形的面积即可解答．
本题考查了平行四边形的性质以及勾股定理，解题的关键是熟练掌握平行四边形的性质并灵活运用．

9.【答案】A 
【解析】解：∵实际每天修建盲道的长度比原计划增加10米，且原计划每天修建盲道x米，
∴实际每天修建盲道(x+10)米．
根据题意得：1120x−1120x+10=2．
故选：A．
根据实际及原计划工作效率间的关系，可得出实际每天修建盲道(x+10)米，利用工作时间=工作总量÷工作效率，结合实际比原计划提前2天完成修建任务，即可列出关于x的分式方程，此题得解．
本题考查了由实际问题抽象出分式方程，找准等量关系，正确列出分式方程是解题的关键．

10.【答案】B 
【解析】解：过C作CK//l1，过A作AH⊥CK，交l1于M，交l2于N，作CP⊥l2于P，
∵l1//l2，
∴CK//l2，
∴AH⊥l1，AH⊥l2，
∴AM=2，MN=4，
由题意得：BC=AD，CD=AB，
∴四边形ABCD是平行四边形，
∴AB//CD，∠BAM=∠QCD，AB=CD，
∵l1//l2，
∴∠ABM=∠CDQ，
∴△ABM≌△CDQ(ASA)，
∴CP=AM=2，
∴HN=CP=2，
∴AH=2+4+2=8，
∵AC≥AH，
∴点A与点C之间距离的最小值是8．
故选：B．
过C作CK//l1，过A作AH⊥CK，交l1于M，交l2于N，作CP⊥l2于P，得到CK//l2，因此AM=2，MN=4，由平行四边形的性质推出，△ABM≌△CDQ(ASA)，CP=AM=2，得到HN=2，求出AH=8，由AC≥AH，即可求出AC的最小值．
本题考查平行线之间的距离，点到直线的距离，关键是通过作辅助线，得到AC≥AH，求出HN即可解决问题．

11.【答案】a(a+1)2 
【解析】解：a3+2a2+a
=a(a2+2a+1)
=a(a+1)2，
故答案为：a(a+1)2
原式提取公因式，再利用完全平方公式分解即可．
此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．

12.【答案】146a 
【解析】解：∵路程=速度×时间，
∴高铁的速度是每小时146a千米，
故答案为：146a．
根据“路程=速度×时间”进行变式、求解．
此题考查了列代数式表示实际问题的能力，关键是能准确理解并运用实际问题间的数量关系．

13.【答案】四 
【解析】
【分析】
本题考查了多边形的外角和定理以及四边形的内角和定理，比较简单．利用多边形的外角和以及四边形的内角和定理即可解决问题．
【解答】
解：∵多边形的外角和是360度，多边形的内角和等于它的外角和，则内角和是360度，
∴这个多边形是四边形．
故答案为四．  
14.【答案】x0的解集是x