九年级下册第一章 直角三角形的边角关系5 三角函数的应用精品综合训练题

专题1.5  解直角三角函数应用-坡度坡角应用（专项训练）

1．（•济阳区期末）如图，一山坡的坡度i＝1：，小明从A处爬到B处所走的直线距离AB＝100米，则他在垂直方向上升的高度CB为 　 　米．

2. （2021秋•南召县月考）如图所示，某商场要在一楼和二楼之间搭建扶梯BC，已知一楼与二楼之间的地面高度差为3.5米，扶梯BC的坡度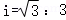，则扶梯BC的长度

为       米．

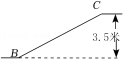
3．（2022•瑶海区三模）图1、图2分别是一滑雪运动员在滑雪过程中某一时刻的实物图与示意图，已知运动员的小腿ED与斜坡AB垂直，大腿EF与斜坡AB平行，且G、E、D三点共线，若雪仗EM长为1m，EF＝0.4m，∠EMD＝30°，∠GFE＝62°，求此刻运动员头部G到斜坡AB的高度h（精确到0.1m，参考数据：sin62°≈0.88、cos62°≈0.47、tan62°≈1.88）

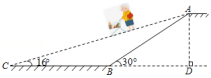
4．（2022•太平区一模）某商场从安全和便利的角度出发，提升顾客的购物体验，准备将自动扶梯由原来的阶梯式改造成斜坡式．如图，已知商场的层高AD为6m，坡角∠ABD为30°，改造后的斜坡式自动扶梯的坡角∠ACB为16°，请你计算改造后的斜坡式自动扶梯AC相比改造前AB增加的长度．（结果精确到0.1m，参考数据：sin16°≈0.28，cos16°≈0.96，tan16°≈0.29）

5．（2022春•北碚区校级月考）如图，为了测量陶行知纪念馆AB的高度，小李在点C处放置了高度为1.5米的测角仪CD，测得纪念馆顶端A点的仰角∠ADE＝51°，然后他沿着坡度i＝1：2.4的斜坡CF走了6.5米到达点F，再沿水平方向走4米就到达了纪念馆底端点B．（结果精确到0.1，参考数据：sin51°≈0.78，cos51°≈0.63，tan51°≈1.23）

（1）求点D到纪念馆AB的水平距离；

（2）求纪念馆AB的高度约为多少米？

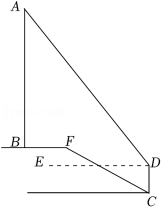
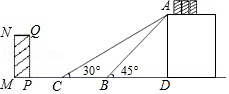
6．（2022•黄岩区一模）如图是某货站传送货物的平面示意图，为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．已知原传送带AB长为4m．

（1）求新传送带AC的长度；

（2）如果需要在货物着地点C的左侧留出5m的通道，试判断距离B点4m的货物MNQP是否需要挪走，并说明理由．

7．（2022•铁岭模拟）某小区开展了“行车安全，方便居民”的活动，对地下车库作了改进．如图，这小区原地下车库的入口处有斜坡AC长为13米，它的坡度为i＝1：2.4，AB⊥BC，为了居民行车安全，现将斜坡的坡角改为13°，即∠ADC＝13°（此时点B、C、D在同一直线上）．

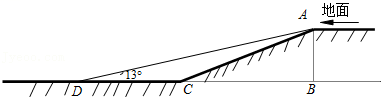
（1）求这个车库的高度AB；

（2）求斜坡改进后的起点D与原起点C的距离（结果精确到0.1米）．

（参考数据：sin13°≈0.225，cos13°≈0.974，tan13°≈0.231，cot13°≈4.331）

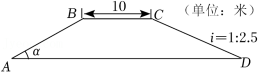
8.（2022•瑶海区二模）2021年底中国高铁运营里程数已达4万公里，中国高铁发展速度之快、质量之高令全世界惊叹，是当之无愧的“国家名片”．如图所示某条高铁路基的横断面是四边形ABCD，AD∥BC，路基顶BC宽10米，斜坡AB长为15米，斜坡AB的坡角α是32°，斜坡CD的坡度i＝1：2.5，求路基底AD的长．（结果精确到1米，参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62）

9.（2022春•渝中区校级月考）图1是安装在倾斜屋顶上的热水器，图2是安装热水器的侧面示意图．已知屋面AE的倾斜角∠EAD为22°，长为3米的真空管AB与水平线AD的夹角为37°，安装热水器的铁架竖直管CE的长度为0.5米．

（1）真空管上端B到水平线AD的距离．

（2）求安装热水器的铁架水平横管BC的长度（结果精确到0.1米）．

（参考数据：sin37°≈，cos37°≈，tan37°≈，sin22°≈，cos22°≈，tan22°≈0.4）

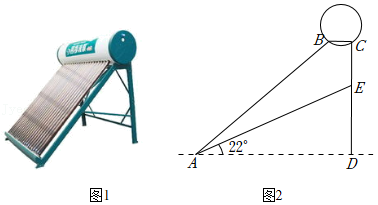
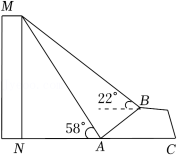
10．（2022•营口）在一次数学课外实践活动中，某小组要测量一幢大楼MN的高度，如图，在山坡的坡脚A处测得大楼顶部M的仰角是58°，沿着山坡向上走75米到达B处，在B处测得大楼顶部M的仰角是22°，已知斜坡AB的坡度i＝3：4（坡度是指坡面的铅直高度与水平宽度的比），求大楼MN的高度．（图中的点A，B，M，N，C均在同一平面内，N，A，C在同一水平线上，参考数据：tan22°≈0.4，tan58°≈1.6）

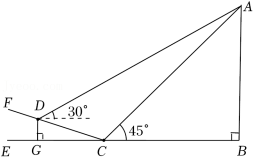
11．（2022•鄂州）亚洲第一、中国唯一的航空货运枢纽——鄂州花湖机场，于2022年3月19日完成首次全货运试飞，很多市民共同见证了这一历史时刻．如图，市民甲在C处看见飞机A的仰角为45°，同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°．若斜坡CF的坡比＝1：3，铅垂高度DG＝30米（点E、G、C、B在同一水平线上）．求：

（1）两位市民甲、乙之间的距离CD；

（2）此时飞机的高度AB．（结果保留根号）

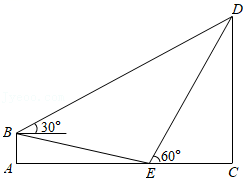
12．（2021•内江）在一次课外活动中，某数学兴趣小组测量一棵树CD的高度．如图所示，测得斜坡BE的坡度i＝1：4，坡底AE的长为8米，在B处测得树CD顶部D的仰角为30°，在E处测得树CD顶部D的仰角为60°，求树高CD．（结果保留根号）

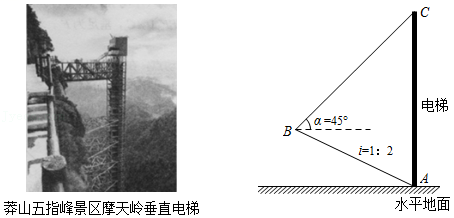
13．（2021•郴州）如图，莽山五指峰景区新建了一座垂直观光电梯．某测绘兴趣小组为测算电梯AC的高度，测得斜坡AB＝105米，坡度i＝1：2，在B处测得电梯顶端C的仰角α＝45°，求观光电梯AC的高度．

（参考数据：≈1.41，≈1.73，≈2.24．结果精确到0.1米）