

- 专题3.1 圆(知识解读)-2023-2024学年九年级数学下册《同步考点解读•专题训练》(北师大版) 试卷 1 次下载
- 专题3.1 圆(能力提升)-2023-2024学年九年级数学下册《同步考点解读•专题训练》(北师大版) 试卷 0 次下载
- 专题3.2 垂直于弦的直径(专项训练)-2023-2024学年九年级数学下册《同步考点解读•专题训练》(北师大版) 试卷 1 次下载
- 专题3.2 垂直于弦的直径(知识解读)-2023-2024学年九年级数学下册《同步考点解读•专题训练》(北师大版) 试卷 1 次下载
- 专题3.3 与圆有关的角(专项训练)-2023-2024学年九年级数学下册《同步考点解读•专题训练》(北师大版) 试卷 0 次下载
初中数学北师大版九年级下册2 圆的对称性优秀练习
展开专题3.2 圆的对称性(能力提升)
一、选择题。
1.(2022秋•邢台期中)如图,已知在⊙O中,BC是直径,AB=DC,则下列结论不一定成立的是( )
A.OA=OB=AB B.∠AOB=∠COD
C. D.O到AB、CD的距离相等
2.(2022秋•平湖市期中)如图,AB是半圆的直径,∠BAC=20°,D是的中点,则∠DAC的度数是( )
A.30° B.35° C.45° D.70°
3.(2022秋•南开区期中)如图,AB是⊙O的直径,点E在⊙O上,点D,C是的三等分点,∠COD=34°,则∠AOE的度数是( )
A.78° B.68° C.58° D.56°
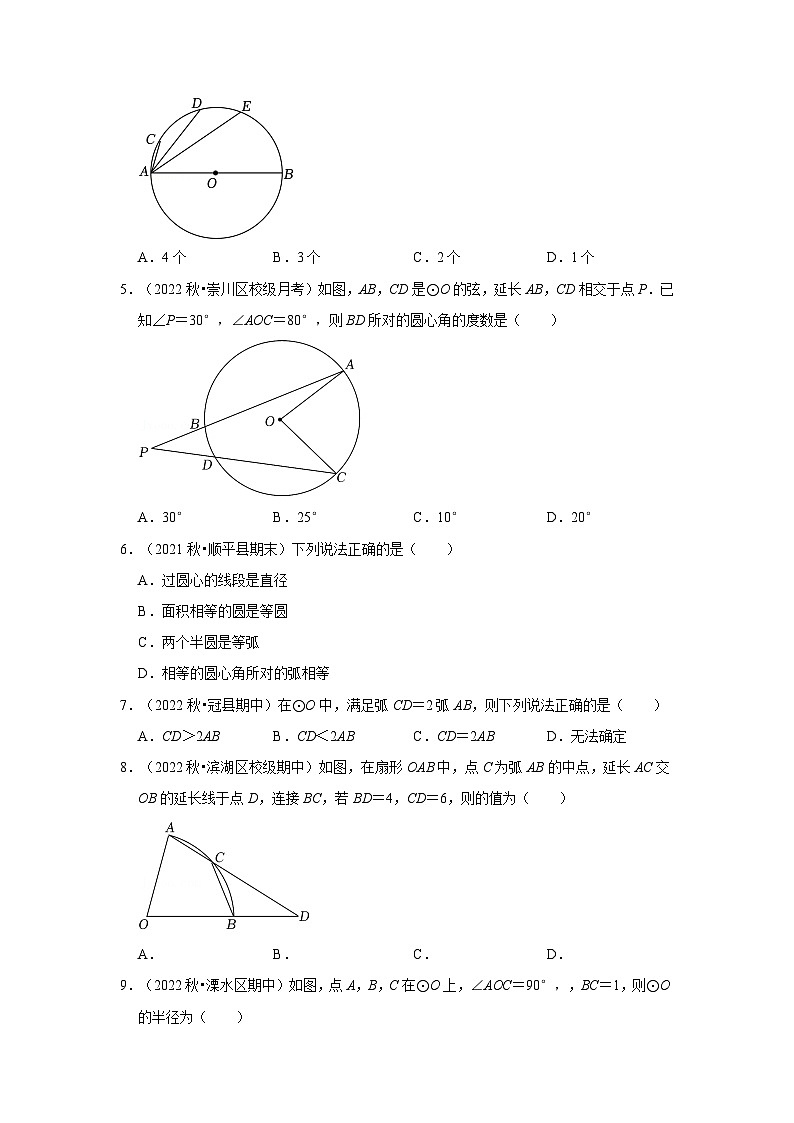
4.(2022秋•玄武区期中)如图,在⊙O中,AB是直径,点C,D,E在圆上,AC=2,AD=6,AE=8,AB=10.下列结论:①;②;③;④,其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
5.(2022秋•崇川区校级月考)如图,AB,CD是⊙O的弦,延长AB,CD相交于点P.已知∠P=30°,∠AOC=80°,则BD所对的圆心角的度数是( )
A.30° B.25° C.10° D.20°
6.(2021秋•顺平县期末)下列说法正确的是( )
A.过圆心的线段是直径
B.面积相等的圆是等圆
C.两个半圆是等弧
D.相等的圆心角所对的弧相等
7.(2022秋•冠县期中)在⊙O中,满足弧CD=2弧AB,则下列说法正确的是( )
A.CD>2AB B.CD<2AB C.CD=2AB D.无法确定
8.(2022秋•滨湖区校级期中)如图,在扇形OAB中,点C为弧AB的中点,延长AC交OB的延长线于点D,连接BC,若BD=4,CD=6,则的值为( )
A. B. C. D.
9.(2022秋•溧水区期中)如图,点A,B,C在⊙O上,∠AOC=90°,,BC=1,则⊙O的半径为( )
A. B. C. D.
10.(2022秋•海州区校级月考)下列说法中,正确的个数为( )
(1)在同圆或等圆中,弦相等则所对的弧相等;
(2)优弧一定比劣弧长;
(3)弧相等则所对的圆心角相等;
(4)在同圆或等圆中,圆心角相等则所对的弦相等.
A.1个 B.2个 C.3个 D.4个
二、填空题。
11.(2022秋•新北区校级月考)如图,在同圆中,若∠AOC=2∠BOD,则AC 2BD.(填“>”“<”或“=”)
12.(2022秋•江宁区月考)若一条弦把圆周分成2:3的两段弧,则劣弧所对圆心角的度数是 .
13.(2022•黄石)如图,圆中扇子对应的圆心角α(α<180°)与剩余圆心角β的比值为黄金比时,扇子会显得更加美观,若黄金比取0.6,则β﹣α的度数是 .
14.(2022•江阴市模拟)如图,AB是⊙O的直径,C为⊙O上异于A、B的点,点E、F分别在AC、BC上且AE=BF,已知AB=6,EF=4,若取EF中点G,连接CG,则CG的长为 ,AE的最小值为 .
15.(2022•成都模拟)如图,四边形ABCD是⊙O内接四边形,BD是⊙O的直径,=,若四边形ABCD的面积是10,则线段AC的长为 .
16.(2022秋•海淀区校级期中)如图,BD是⊙O的直径,C是的中点,若∠AOC=70°,则∠AOD的度数为 .
17.(2022•费县一模)如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为120°的多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒米的速度沿曲线向右运动,则在第2022秒时点P的坐标为 .
18.(2022秋•萧山区期中)如图,在半圆O中半径为,=,=,BM与AN交于点D,
(1)∠ADM= ;
(2)当点D恰好为BM的中点时,AM= .
三、解答题。
19.(2022秋•垦利区期中)如图,AB为⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠C=23°,试求∠EOB的度数.
20.(2022秋•涟水县校级月考)如图,在△ABC中,AB=AC,∠A=40°,以点B为圆心,BC长为半径的圆交AB于点D,交AC于点E,求弧DE的度数.
21.(2021秋•藤县期末)如图,OA,OB,OC是⊙O的半径,=,CD⊥OA于D,CE⊥OB于E.求证:AD=BE.
22.(2022秋•桐庐县期中)如图,AB为⊙O的直径,半径OC∥弦BD,判断与是否相等,并说明理由.
23.(2022秋•南京期中)如图,⊙O的弦AB、CD相交于点E,AB=CD,求证:AE=CE.
24.(2022秋•瑞安市期中)已知:如图,AB,DE是⊙O的直径,C是⊙O上一点,且BE=CE.
求证:.
25.(2022•合肥模拟)如图,四边形ABCD内接于⊙O,AB为直径,所对圆心角为90°,连接AC,BD交于点E.
(1)求证:BC=CE;
(2)当DC=时,求⊙O的半径.
26.(2022秋•靖江市期中)如图,在⊙O中,AB为直径,延长AB至点P,C是⊙O上一点,连接PC并延长交⊙O于点D.
(1)若::=1:2:3,⊙O的半径为2,求弦CD的长;
(2)若⊙O的半径为3,OP=4,∠AOD=90°,求弦CD的长.
专题3.2 圆的对称性(能力提升)
一、选择题。
1.(2022秋•邢台期中)如图,已知在⊙O中,BC是直径,AB=DC,则下列结论不一定成立的是( )
A.OA=OB=AB B.∠AOB=∠COD
C. D.O到AB、CD的距离相等
【答案】A。
【解答】解:∵AB=DC,
∴弧AB=弧DC,
∴∠AOB=∠COD,
∵OA=OB=OC=OD,
∴△AOB≌△COD(SAS),
∴O到AB、CD的距离相等,
所以B、C、D选项正确,
故选:A.
2.(2022秋•平湖市期中)如图,AB是半圆的直径,∠BAC=20°,D是的中点,则∠DAC的度数是( )
A.30° B.35° C.45° D.70°
【答案】B。
【解答】解:连接BC,
∵AB是半圆的直径,
∴∠C=90°,
∵∠BAC=20°,
∴∠CBA=90°﹣∠BAC=70°,
∵D是的中点,
∴∠DAC=∠ABC=35°.
故选:B.
3.(2022秋•南开区期中)如图,AB是⊙O的直径,点E在⊙O上,点D,C是的三等分点,∠COD=34°,则∠AOE的度数是( )
A.78° B.68° C.58° D.56°
【答案】A。
【解答】解:∵点D、C是的三等分点,
即==,
∴∠BOC=∠COD=∠DOE=34°,
∴∠AOE=180°﹣3×34°=78°.
故选:A.
4.(2022秋•玄武区期中)如图,在⊙O中,AB是直径,点C,D,E在圆上,AC=2,AD=6,AE=8,AB=10.下列结论:①;②;③;④,其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
【答案】B。
【解答】解:连接CE、DB,如图,
∵AC=2,AE=8,
∴CE>AE﹣AC,即CE>6,
而AD=6,
∴AD<CE,
∴<,所以①错误;
∵AB是直径,
∴∠ADB=90°,
∴BD===8,
∵AE=BD=8,
∴=,所以②正确;
+=,所以③正确;
∵=,
∴+=+=,所以④正确.
故选:B.
5.(2022秋•崇川区校级月考)如图,AB,CD是⊙O的弦,延长AB,CD相交于点P.已知∠P=30°,∠AOC=80°,则BD所对的圆心角的度数是( )
A.30° B.25° C.10° D.20°
【答案】D。
【解答】解:如图,连接BC,
∵∠AOC=80°,
∴∠ABC=∠AOC=40°,
∵∠P=30°,∠ABC=∠P+∠BCD,
∴∠BCD=10°,
∴BD所对的圆心角的度数的度数20°.
故选:D.
6.(2021秋•顺平县期末)下列说法正确的是( )
A.过圆心的线段是直径
B.面积相等的圆是等圆
C.两个半圆是等弧
D.相等的圆心角所对的弧相等
【答案】B。
【解答】解:A.过圆心且两个端点在圆上的线段是直径,故A选项说法错误;
B.面积相等的圆,则半径相等,是等圆,故B选项说法正确;
C.在同圆或等圆中,两个半圆是等弧,故C选项说法错误;
D.在同圆或等圆中,相等的圆心角所对的弧相等,故C选项说法错误;
故选:B.
7.(2022秋•冠县期中)在⊙O中,满足弧CD=2弧AB,则下列说法正确的是( )
A.CD>2AB B.CD<2AB C.CD=2AB D.无法确定
【答案】B。
【解答】解:如图,过O点作半径OE⊥CD,则=,
∵=2,
∴==,
∴AB=CE=DE,
∵CE+DE>CD,
∴2AB>CD.
故选:B.
8.(2022秋•滨湖区校级期中)如图,在扇形OAB中,点C为弧AB的中点,延长AC交OB的延长线于点D,连接BC,若BD=4,CD=6,则的值为( )
A. B. C. D.
【答案】B。
【解答】解:连接OC,
∵点C为弧AB的中点,
∴∠AOC=∠BOC,OA=OC=OB,
∴△AOC≌△BOC(SAS),
∴∠A=∠OBC=∠OCA=∠OCB,
又∠DBC=∠DCO,
∴△DBC∽△DCO(AA),
∴,
∵BD=4,CD=6,
∴=,
解得:DO=9,
∴OB=OD﹣BD=9﹣4=5,
∴=
∴=,
=,
故选:B.
9.(2022秋•溧水区期中)如图,点A,B,C在⊙O上,∠AOC=90°,,BC=1,则⊙O的半径为( )
A. B. C. D.
【答案】C。
【解答】解:过点A作AE⊥CB交CB的延长线于点E,连接AC.
∵∠AOC=90°,
∴∠ABC=(360°﹣90°)=135°,
∴∠ABE=45°,
∵∠E=90°,AB=,
∴AE=EB=1,
∵BC=1,
∴EC=2,
∴AC===,
∴OA=OC=AC=.
故选:C.
10.(2022秋•海州区校级月考)下列说法中,正确的个数为( )
(1)在同圆或等圆中,弦相等则所对的弧相等;
(2)优弧一定比劣弧长;
(3)弧相等则所对的圆心角相等;
(4)在同圆或等圆中,圆心角相等则所对的弦相等.
A.1个 B.2个 C.3个 D.4个
【答案】B。
【解答】解:(1)在同圆或等圆中,弦相等则所对的弧相等,错误,弦所对的弧有优弧或劣弧,不一定相等.
(2)优弧一定比劣弧长,错误,条件是同圆或等圆中;
(3)弧相等则所对的圆心角相等.正确;
(4)在同圆或等圆中,圆心角相等则所对的弦相等.正确;
故选:B.
二、填空题。
11.(2022秋•新北区校级月考)如图,在同圆中,若∠AOC=2∠BOD,则AC < 2BD.(填“>”“<”或“=”)
【答案】<。
【解答】解:如图,以OD为边作∠DOE=∠BOD,OE与⊙O交于点E,连接AC、BE、BD、ED,
则∠BOE=2∠BOD,BD=DE,
∵∠AOC=2∠BOD,
∴∠AOC=∠BOE,
∴AC=BE,
在△BDE中,BE<BD+ED=2BD,
∴AC<2BD,
故答案为:<.
12.(2022秋•江宁区月考)若一条弦把圆周分成2:3的两段弧,则劣弧所对圆心角的度数是 144° .
【答案】144°。
【解答】解:∵一条弦把圆周分成2:3的两段弧,
∴劣弧所对圆心角的度数为360°×=144°.
故答案为:144°.
13.(2022•黄石)如图,圆中扇子对应的圆心角α(α<180°)与剩余圆心角β的比值为黄金比时,扇子会显得更加美观,若黄金比取0.6,则β﹣α的度数是 90° .
【答案】90°。
【解答】解:根据题意得:,
解得,
∴β﹣α=225°﹣135°=90°,
故答案为:90°.
14.(2022•江阴市模拟)如图,AB是⊙O的直径,C为⊙O上异于A、B的点,点E、F分别在AC、BC上且AE=BF,已知AB=6,EF=4,若取EF中点G,连接CG,则CG的长为 2 ,AE的最小值为 .
【答案】2,。
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵G是EF的中点,
∴CG=EF=2,
点G到圆上的距离始终为2,即点G在以O为圆心,3﹣2=1为半径的半圆上运动,
∴当AC=BC时,此时AE=BF最小,如图,
则CE=CF,AC=BC=,
∴,
∴EF∥AB,
∴△CEF∽△CAB,
∴,
即,
解得:CE=2,
∴AE=,
故答案为:2,.
15.(2022•成都模拟)如图,四边形ABCD是⊙O内接四边形,BD是⊙O的直径,=,若四边形ABCD的面积是10,则线段AC的长为 2 .
【答案】2。
【解答】解:∵BD为⊙O的直径,
∴∠BAD=90°,
∵,
∴AB=AD,
∵∠CBD=∠CAD,∠ABD=∠ACD,
∴∠CBD+∠ABD=∠CAD+∠ACD,
即∠ABC=∠ADE,
作AE⊥AC交CD的延长线于点E,
∴∠CAE=∠BAD=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC=90°,
∴∠BAC=∠DAE,
∴△ABC≌△ADE(AAS),
∴AC=AE,S△ABC=S△ADE,
∴S四边形ABCD=S△ABC+S△ACD=S△ADE+S△ACD=S△ACE=AC•AE=AC2=10,
∴AC=,
故答案为:2.
16.(2022秋•海淀区校级期中)如图,BD是⊙O的直径,C是的中点,若∠AOC=70°,则∠AOD的度数为 40° .
【答案】40°。
【解答】解:∵C是的中点,
∵=.
∵∠AOC=70°,
∴∠AOC=∠BOC=70°.
∵BD是⊙O的直径,
∴∠AOD+∠AOC+∠BOC=180°.
∴∠AOD=40°.
故答案为:40°.
17.(2022•费县一模)如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为120°的多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒米的速度沿曲线向右运动,则在第2022秒时点P的坐标为 (2022,0) .
【答案】(2022,0)。
【解答】解:如图,过点O作OC⊥AB,垂足为C,则AC=BC,
在Rt△AOC中,∠AOC=∠BOC=×120°=60°,OA=OB=2米,
∴AC=×2=(米),
∴AB=2(米),
的长为=π(米),
∴AP=2×[(π×2022)÷(π)]
=2×1011
=2022(米),
∴点P的坐标为(2022,0),
故答案为:(2022,0).
18.(2022秋•萧山区期中)如图,在半圆O中半径为,=,=,BM与AN交于点D,
(1)∠ADM= 60° ;
(2)当点D恰好为BM的中点时,AM= 2 .
【答案】2。
【解答】解:(1)∵=,=,
∴+=+=(+)=,
∴=,
∴∠MAN=30°,
∵AB为圆O的直径,
∴∠M=90°,
∴∠ADM=60°;
故答案为:60°;
(2)设MD=x,
∵点D恰好为BM的中点,
∴MB=2MD=2x,
在Rt△AMD中,∠MAD=30°,
∴AM=MD=x,
在Rt△AMB中,根据勾股定理得,
AM2+MB2=AB2,
即(x)2+(2x)2=(2)2,
解得x=2(舍去x=﹣2),
∴AM=x=2.
故答案为:2.
三、解答题。
19.(2022秋•垦利区期中)如图,AB为⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠C=23°,试求∠EOB的度数.
【解答】解:∵CD=OA=OD,∠C=23°,
∴∠ODE=2∠C=46°,
∵OD=OE,
∴∠E=∠EDO=46°,
∴∠EOB=∠C+∠E=46°+23°=69°.
20.(2022秋•涟水县校级月考)如图,在△ABC中,AB=AC,∠A=40°,以点B为圆心,BC长为半径的圆交AB于点D,交AC于点E,求弧DE的度数.
【解答】解:连接BE,如图,
∵AB=AC,∠A=40°,
∴∠ABC=∠C=(180°﹣∠A)=×(180°﹣40°)=70°,
∵BE=BC,
∴∠BEC=∠C=70°,
∵∠BEC=∠A+∠ABE,
∴∠ABE=70°﹣40°=30°,
∴弧DE的度数为30°.
21.(2021秋•藤县期末)如图,OA,OB,OC是⊙O的半径,=,CD⊥OA于D,CE⊥OB于E.求证:AD=BE.
【解答】证明:∵=,
∴∠AOC=∠BOC,
∴OC平分∠AOB,
∵CD⊥OA,CE⊥OB,
∴CD=CE,
∵OC=OC,
∴Rt△COD≌Rt△COE(HL),
∴OD=OE,
∵OA=OB,
∴OA﹣OD=OB﹣OE,
∴AD=BE.
22.(2022秋•桐庐县期中)如图,AB为⊙O的直径,半径OC∥弦BD,判断与是否相等,并说明理由.
【解答】解:相等,
理由:如图,连接OD,
∵OC∥BD,
∴∠AOC=∠B,∠COD=∠D,
∵OB=OD,
∴∠D=∠B,
∴∠AOC=∠COD,
∴=.
23.(2022秋•南京期中)如图,⊙O的弦AB、CD相交于点E,AB=CD,求证:AE=CE.
【解答】证明:如图,连接AC,AD,BC,
∵AB=CD,
∴=,
∴﹣=﹣,
即=,
∴∠BAC=∠ACD,
∴AE=CE.
24.(2022秋•瑞安市期中)已知:如图,AB,DE是⊙O的直径,C是⊙O上一点,且BE=CE.
求证:.
【解答】证明:∵圆心角∠BOE=圆心角∠AOD,
∴=,
∵BE=CE,
=,
∴=.
25.(2022•合肥模拟)如图,四边形ABCD内接于⊙O,AB为直径,所对圆心角为90°,连接AC,BD交于点E.
(1)求证:BC=CE;
(2)当DC=时,求⊙O的半径.
【解答】(1)证明:∵所对圆心角为90°,
∴∠DBC=45°,
∵AB为直径,
∴∠ACB=90°,
∴∠CEB=45°,
∴∠CEB=∠DBC,
∴BC=CE;
(2)解:∵∠ECB=90°,CE=CB,
∴△CEB是等腰直角三角形,
∴BE=CE,
∵∠DCE=∠ABE,∠CDE=∠BAE,
∴△DCE∽△ABE,
∴,
∵DC=,
∴,
∴AB=2,
∴⊙O的半径为1.
解法二:连接OD,OC,则OD=OC.又∵弧DC所对的圆心角为90°,
∴△DOC为等腰直角三角形,
∵DC=,
∴OD=OC=1,即⊙O的半径为1.
26.(2022秋•靖江市期中)如图,在⊙O中,AB为直径,延长AB至点P,C是⊙O上一点,连接PC并延长交⊙O于点D.
(1)若::=1:2:3,⊙O的半径为2,求弦CD的长;
(2)若⊙O的半径为3,OP=4,∠AOD=90°,求弦CD的长.
【解答】解:(1)如图,连接OC,
∵AB是⊙O的直径,::=1:2:3,
∴∠BOC=180°×=30°,
∠COD=180°×=60°,
∠AOD=180°×=90°,
又∵OC=OD,
∴△COD是正三角形,
∴CD=OC=OD=2;
(2)如图,过点O作OE⊥CD,垂直为E,则CE=DE=CD,
∵∠AOD=90°=∠POD,OD=3,OP=4,
∴PD==5,
∵=cos∠ODE=,
∴=,
解得DE=,
∴CD=2DE=.
初中数学2 圆的对称性精品课后复习题: 这是一份初中数学2 圆的对称性精品课后复习题,共29页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
专题5.2 视图(能力提升)-2023-2024学年九年级数学上册《同步考点解读•专题训练》(北师大版): 这是一份专题5.2 视图(能力提升)-2023-2024学年九年级数学上册《同步考点解读•专题训练》(北师大版),文件包含湖南师大附中数学附中3次pdf、湖南师大附中数学答案附中3次pdf等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。
专题5.1 投影(能力提升)-2023-2024学年九年级数学上册《同步考点解读•专题训练》(北师大版): 这是一份专题5.1 投影(能力提升)-2023-2024学年九年级数学上册《同步考点解读•专题训练》(北师大版),文件包含湖南师大附中数学附中3次pdf、湖南师大附中数学答案附中3次pdf等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。













