初中数学浙教版八年级下册6.1 反比例函数教案及反思

6.1 反比例函数

教学目标

【知识与技能】

    1.理解反比例函数的概念，根据实际问题能列出反比例函数关系式.

   2.利用正比例函数和反比例函数的概念求解简单的函数式．

   【过程与方法】

    经历从实际问题抽象出反比例函数的探索过程，发展学生的抽象思维能力。

【情感态度】

    培养观察、推理、分析能力，体会由实际问题转化为数学模型，认识反比例函数的应用价值.

教学难点

 1、理解反比例函数的概念，能根据已知条件写出函数解析式。

 2、能根据实际问题中的条件确定反比例函数的解析式，体会函数的模型思想。

教学过程

一、问题引入

  某人驾驶汽车从海门到南通，路程全长约为50km，汽车油耗0.1L/km。

（1）若汽车从海门出发行驶x km油耗为Q L，请用含x的代数式表示Q。

Q＝0.1x

（2）若这辆汽车驶离海门时油箱中有油60L，则汽车行驶了x km后油箱的剩油量为P  L，请用含有x 的代数式表示P。

P = 60 - 0.1X

（3）设汽车的速度是匀速的，速度为v km/h，该车从海门到南通所用时间为t  h，你能用含v的代数式表示t 吗？

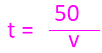
二、探究新知

问题1：小华的爸爸早晨骑自行车带小华到15千米的镇外去赶集，回来时让小华乘公共汽车，用的时间少了．假设两人经过的路程一样，而且自行车和汽车的速度在行驶过程中都不变，爸爸要小华找出从家里到镇上的时间和乘坐不同交通工具的速度之间的关系．

分析：和其他实际问题一样，要探求两个变量之间的关系，就应先选用适当的符号表示变量，再根据题意列出相应的函数关系式．

设小华乘坐交通工具的速度是v千米/时，从家里到镇上的时间是t小时．因为在匀速运动中，时间=路程÷速度，所以t=15/v

从这个关系式中发现:

1.路程一定时，时间t就是速度v的反比例函数．即速度增大了，时间变小；速度减小了，时间增大．

2.自变量v的取值是v＞0．现了什么?

三、合作探究

问题2：学校课外生物小组的同学准备自己动手，用旧围栏建一个面积为24平方米的矩形饲养场．设它的一边长为x(米)，求另一边的长y(米)与x的函数关系式．

分析：根据矩形面积可知

           xy=24，

           即y=24/x

 从这个关系中发现：

1.当矩形的面积一定时，矩形的一边是另一边的反比例函数．即矩形的一边长增大了，则另一边减小；若一边减小了，则另一边增大；

2.自变量的取值是x＞0．观察上述两个函数解析式，它们有什么共同点？与前面学的一次函数有什么不同？

【归纳结论】

一般地，形如y=k/x(k是常数，k≠0)的函数叫做反比例函数.

四、巩固练习

同学们做练习题

五、课堂小结

知识总结