

数学八年级下册6.3 反比例函数的应用导学案
展开6.3 反比例函数的应用
我预学
1.市场上,一些不法商贩在卖货时将秤砣挖空,或更换较小称砣,使砣较轻,从而欺骗顾客.
(1)如图,对于同一物体,哪个图用的是标准秤砣,哪个用的是较轻的秤砣?
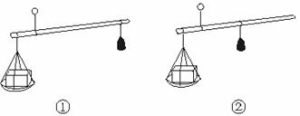
(2)在称同一物体时,所称得的物体质量y(千克)与所用秤砣质量x(千克)之间满足__________关系.
(3)当砣较轻时,称得的物体变重,这正好符合哪个函数的哪些性质?
2. 阅读教材中的本节内容后回答:
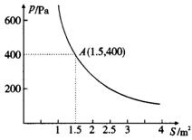 某校科技小组进行野外考察,途中遇到一片十几米宽的料泥地.为了完全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时通道,木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数.
某校科技小组进行野外考察,途中遇到一片十几米宽的料泥地.为了完全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时通道,木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数.
(1)请直接写出这一函数解析式和自变量的取值范围:
(2)当木板面积为0.2平方米时,压强是多少?
(3)如果要求压强不超过6000Pa,,木板的面积至少要多大?
(4)请利用图象对(2)和(3)作出直观解释,并与同伴进行交流.
3. 例题2中,如何来利用实验数据的?可否换成其它的实验数据来做题?例题2重点突显了一种数学的建模方式,具体可概括为哪几步?
我求助:预习后,你或许有些疑问,请写在下面的空白处:
我梳理



个性反思:通过本节课的学习,你一定有很多感想和收获,请写在下面的空白处:
我达标
1. 收音机刻度盘的波长l和频率f分别是用米(m)和千赫兹(kHz)为单位标刻的. 波长l和频率f满足关系式![]() ,这说明波长l越大,频率f就 ( )
,这说明波长l越大,频率f就 ( )
A. 越大 B. 越小 C. 不变 D. 不能确定, 与l的取值范围有关
 2.一批相同型号的衬衣单价在每件60元到80元之间(包括60元和80元).现在用720元钱至少可以买 件衬衣,最多可以买 件衬衣.
2.一批相同型号的衬衣单价在每件60元到80元之间(包括60元和80元).现在用720元钱至少可以买 件衬衣,最多可以买 件衬衣.
3.如图,在平面直角坐标系中,已知点A(1,6), B(2,3), C(3,2).
(1)在平面直角坐标系中描出点A,B,C.
(2)根据你所学过的函数类型判断这三点会同时在哪个函数图
象上,画出你推测的图象草图
(3)求出(2)中你推测的图象的函数解析式,并说明该函数图象一定过这三点.
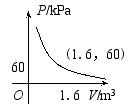
4. 某种气球内充满了一定质量的气体.当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内气体的气压大于120kPa时,气球将爆炸.为了安全,气体的体积应该_________.(写取值)
5. 设矩形ABCD的AB的长为x(cm),BC的长为y(cm),矩形ABCD的面积为常数.已知当AB的长为5cm时,BC的长为7.2cm.
(1)求y关于x的函数关系式和矩形ABCD的面积.
(2)画出函数图象,利用函数图象求出当2<x<9时,y的取值范围.
(3)求当x=6时,矩形ABCD的形状有何变化?请说明理由.
我挑战
6. 某商场出售一批进价为2元的贺卡,在市场营销中发现,此商品的日销售单价x(单位:元)与日销售数量y(单位:张)之间有如下关系:
(1)根据表中数据在平面直角坐标系中描出实数对(x,y)的对应点;
(2)确定y与x之间的函数关系式,并画出图象;
(3)设销售此贺卡的日纯利润为w元,试求出w与x之间的函数关系式.若物价局规定该贺卡售价最高不超过10元/张,请你求出日销售单价x定为多少元时,才能获得最大日销售利润?
我登峰
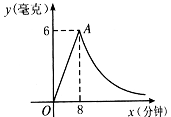
7.为了预防“流感”,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间t(分钟)成正比例,药物燃烧后,y与x成反比例,如图所示.现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x的函数关系式是什么?并指出自变量的取值范围.
(2)药物燃烧后,y关于x的函数关系式是什么?
(3)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才可回到教室;
(4)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?

初中数学浙教版八年级下册第六章 反比例函数6.3 反比例函数的应用学案: 这是一份初中数学浙教版八年级下册第六章 反比例函数6.3 反比例函数的应用学案,共4页。学案主要包含了学习目标,学习重难点,学习过程,达标检测等内容,欢迎下载使用。
浙教版八年级下册6.3 反比例函数的应用学案设计: 这是一份浙教版八年级下册6.3 反比例函数的应用学案设计,共3页。学案主要包含了学习目标,预习领航,新知导学,课内练习等内容,欢迎下载使用。
初中数学浙教版八年级下册6.3 反比例函数的应用学案: 这是一份初中数学浙教版八年级下册6.3 反比例函数的应用学案,共3页。学案主要包含了学习过程等内容,欢迎下载使用。













