初中数学浙教版八年级下册第六章 反比例函数6.3 反比例函数的应用学案

6.3 反比例函数的应用

【学习目标】

1．体验由表格数据建立反比例函数模型的一般过程，体会建模思想

2．会综合运用反比例函数的表达式、函数图像以及性质解决实际问题

3．在实际问题中体验数形结合的思想

【学习重难点】

重点：用反比例函数表达式和图像表示实际问题中成反比例的量之间的关系，并学会利用图像及性质解决问题

难点：较复杂实际问题中反比例函数模型的建立

【学习过程】

一、复习回顾

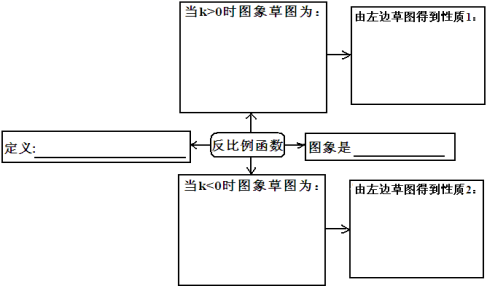
二、解决问题

【问题1】用若干根火柴首尾相接摆成一个矩形，设一根火柴的长度为1，矩形两条邻边的长分别为x，y，要求摆成的矩形的面积为12。

（1）求y关于x的函数表达式和自变量x的取值范围。

（2）该矩形的周长有最大值和最小值吗？若有，请求出来；若没有，请说明理由。

（3）能否摆成正方形？请说明理由。

【问题2】仔细阅读课本例1，解答本小题：设△ABC中BC边的长为x(cm)，BC上的高线AD为y(cm)，△ABC 的面积为常数。已知y关于x的函数图像经过(2，3)。

（1）求y关于x的函数表达式和△ABC的面积。

（2）在右边给定的直角坐标系中画出函数的图像

（3）求当时y的取值范围。

（4）求当时x的取值范围。

【问题3】仔细阅读课本例2，结合下表，思考以下问题：

（1）为了求出压强P(kPa)关于体积V(mL)的函数表达式，你认为怎样处理表中的数据比较合适？

（2）当压强为86 kPa时，体积为多少mL？

（3）若压强，估计气缸内气体体积的取值范围，并说明理由。

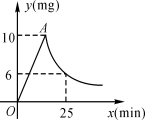
【问题4】已知药物在燃烧机释放过程中，室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分)，根据图像所示信息，解答下列问题：

（1）写出从药物释放开始，y与x之间的函数关系式及自变量的取值范围；

（2）据测定，当空气中每立方米的含药量低于2毫克时，对人体无毒害作用，那么从消毒开始，至少在多长时间内，师生不能进入教室？

【达标检测】

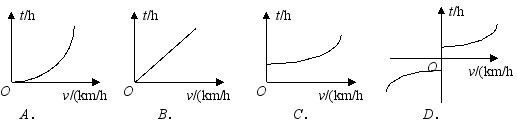
1．已知甲、乙两地相距（km），汽车从甲地匀速行驶到乙地，则汽车行驶的时间（h）与行驶速度（km/h）的函数关系图像大致是（    ）

2．点M（1，a）是一次函数y=3x+2与反比例函数 图像的公共点，若将一次函数y=3x+2的图像向下平移4个单位，则它与反比例函数图像的交点坐标为                     

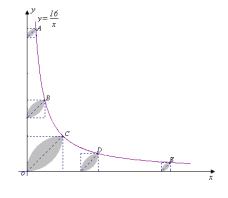
3．已知，A、B、C、D．E是反比例函数（x>0）图像上五个整数点（横、纵坐标均为整数），分别以这些点向横轴或纵轴作垂线段，由垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图5所示的五个橄榄形（阴影部分），则这五个橄榄形的面积总和是            （用含π的代数式表示）