




还剩9页未读,
继续阅读
初中数学浙教版八年级下册5.3 正方形授课ppt课件
展开
这是一份初中数学浙教版八年级下册5.3 正方形授课ppt课件,共17页。PPT课件主要包含了正方形有什么性质,三个角是直角,四条边相等,一个角是直角,或对角线相等,一组邻边相等,或对角线垂直,证题思路分析,过程欣赏等内容,欢迎下载使用。
1、 知道正方形的判定方法,会运用平行四边形、矩形、菱形、正方形的判定条件进行有关的论证和计算. 2、 经历探究正方形判定条件的过程,发展学生初步的综合推理能力,主动探究的学习习惯,逐步掌握说理的基本方法. 3、 理解特殊的平行四边形之间的内在联系,培养学生辩证看问题的观点.
重点:掌握正方形的判定条件. 难点:合理恰当地利用特殊平行四边形的判定进行有关的论证和计算.
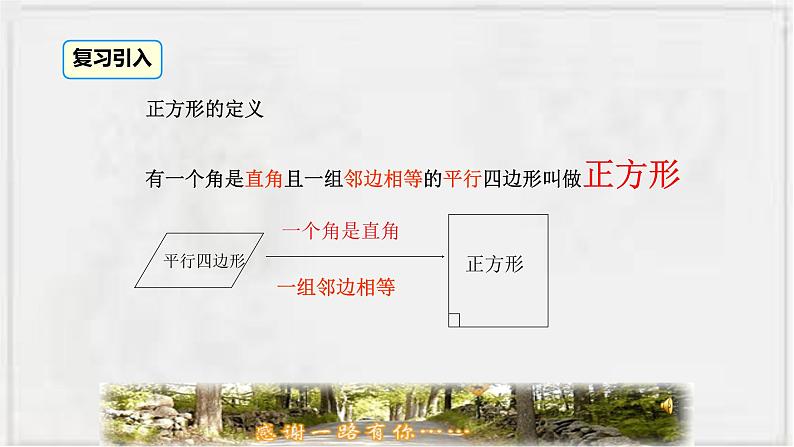
有一个角是直角且一组邻边相等的平行四边形叫做正方形
正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角
正方形的对边平行且相等
正方形的四个角都是直角
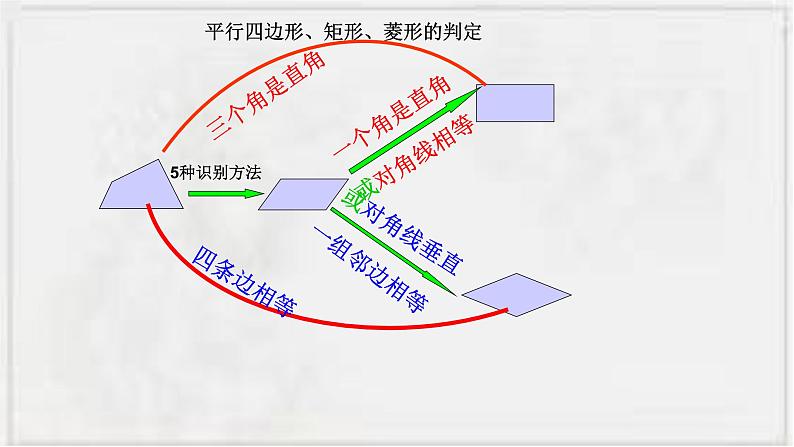
平行四边形、矩形、菱形的判定
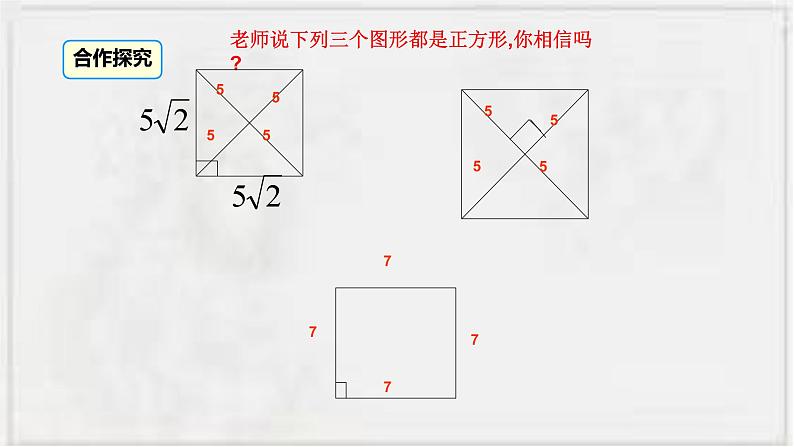
老师说下列三个图形都是正方形,你相信吗?
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是矩形又是菱形(或者既是菱形又是矩形)的四边形是正方形。
两条对角线互相垂直平分且相等的四边形是正方形。
你能总结出正方形有哪些判定方法吗?
1)一组邻边相等的矩形是正方形 2) 有一个角是直角的菱形是正方形
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是菱形又是矩形的四边形是正方形。
例1、如图点A' 、 B' 、 C'、D'分别是正方形ABCD、四条边上的点,并且AA'=BB'=CC'=DD'求证:四边形A'B'C'D'是正方形
①、由已知正方形证三角形全等;②、证得菱形;③、再证直角; ④、是正方形
①证明是正方形就先证是 菱形即证四边相等②再证又是矩形即只证明有个角是直角
证明:∵四边形ABCD是正方形
又∵A`A=B`B=C`C=D`D
∵∠A=∠B=∠C=∠D=90°
∴四边形A`B`C`D`是菱形
又∵∠AD`A`=∠BA`B`, ∠ AA`D`+∠AD`A`=90°
∵∠D`A`B`=180°—(∠AA`D`+∠BA`B`)=90°
∴AB=BC=CD=DA
∴D`A=A`B=B`C=C`D
∴△AA`D`≌△BB`A`≌△CC`B`≌△DD`C`A`D`=A`B`=B`C`=C`D`
∴ ∠AA`D`+∠BA`B`=90 °
∴四边形A`B`C`D`是正方形
例2、△ABC中, ∠ACB=90°,CD平分∠ACB, DE ⊥BC,DF ⊥AC,垂足分别为E,F. 求证:四边形CFDE是正方形.
要证明四边形CFDE是正放形,可以先证四边形CFDE是矩形,然后再证明有一组邻边相等;也可以先证四边形CFDE是菱形,然后再证有一个角是直角.
∵CD平分∠ACB, DE⊥BC,DF ⊥AC
又∵ ∠ DEC= ∠ ECF= ∠ CFD =90°,
∴四边形 CFDE是矩形
∴四边形 CFDE是正方形
想一想:你能用另外一种方法完成证明吗?
(角平分线上的点到角的两边的距离相等)
(有三个角是直角的四边形是矩形),
(有一组邻边相等的矩形是正方形).
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
? 的四边形是正方形
2 、已知:如图,正方形ABCD和正方形CEFG,延长CD到H,且DH=CE=BK。求证:四边形AKFH是一个正方形
3、在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到_____________
1、 知道正方形的判定方法,会运用平行四边形、矩形、菱形、正方形的判定条件进行有关的论证和计算. 2、 经历探究正方形判定条件的过程,发展学生初步的综合推理能力,主动探究的学习习惯,逐步掌握说理的基本方法. 3、 理解特殊的平行四边形之间的内在联系,培养学生辩证看问题的观点.
重点:掌握正方形的判定条件. 难点:合理恰当地利用特殊平行四边形的判定进行有关的论证和计算.
有一个角是直角且一组邻边相等的平行四边形叫做正方形
正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角
正方形的对边平行且相等
正方形的四个角都是直角
平行四边形、矩形、菱形的判定
老师说下列三个图形都是正方形,你相信吗?
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是矩形又是菱形(或者既是菱形又是矩形)的四边形是正方形。
两条对角线互相垂直平分且相等的四边形是正方形。
你能总结出正方形有哪些判定方法吗?
1)一组邻边相等的矩形是正方形 2) 有一个角是直角的菱形是正方形
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是菱形又是矩形的四边形是正方形。
例1、如图点A' 、 B' 、 C'、D'分别是正方形ABCD、四条边上的点,并且AA'=BB'=CC'=DD'求证:四边形A'B'C'D'是正方形
①、由已知正方形证三角形全等;②、证得菱形;③、再证直角; ④、是正方形
①证明是正方形就先证是 菱形即证四边相等②再证又是矩形即只证明有个角是直角
证明:∵四边形ABCD是正方形
又∵A`A=B`B=C`C=D`D
∵∠A=∠B=∠C=∠D=90°
∴四边形A`B`C`D`是菱形
又∵∠AD`A`=∠BA`B`, ∠ AA`D`+∠AD`A`=90°
∵∠D`A`B`=180°—(∠AA`D`+∠BA`B`)=90°
∴AB=BC=CD=DA
∴D`A=A`B=B`C=C`D
∴△AA`D`≌△BB`A`≌△CC`B`≌△DD`C`A`D`=A`B`=B`C`=C`D`
∴ ∠AA`D`+∠BA`B`=90 °
∴四边形A`B`C`D`是正方形
例2、△ABC中, ∠ACB=90°,CD平分∠ACB, DE ⊥BC,DF ⊥AC,垂足分别为E,F. 求证:四边形CFDE是正方形.
要证明四边形CFDE是正放形,可以先证四边形CFDE是矩形,然后再证明有一组邻边相等;也可以先证四边形CFDE是菱形,然后再证有一个角是直角.
∵CD平分∠ACB, DE⊥BC,DF ⊥AC
又∵ ∠ DEC= ∠ ECF= ∠ CFD =90°,
∴四边形 CFDE是矩形
∴四边形 CFDE是正方形
想一想:你能用另外一种方法完成证明吗?
(角平分线上的点到角的两边的距离相等)
(有三个角是直角的四边形是矩形),
(有一组邻边相等的矩形是正方形).
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
? 的四边形是正方形
2 、已知:如图,正方形ABCD和正方形CEFG,延长CD到H,且DH=CE=BK。求证:四边形AKFH是一个正方形
3、在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到_____________













